1. 引言
经典的开放式渔场自反馈捕捞模型 [1] 如下所示:
(1)
其中,s表示t时刻某类鱼种群的密度或数量,E表示t时刻捕捞努力量,p表示价格,w表示单位投入的成本,v是正常数,表示捕捞努力量与净利润的大小成正比。
但是在市场经济中,商品的价格会受供求关系影响,通常的价格 [3] - [9] 满足
其中,s表示鱼的市场投放量,m,n均为正常数。m刻画消费者需求程度,需求越大,m越小;n表示商品最大价格。显然
即当市场投放量(捕捞量)很少时,市场价格昂贵;当市场投放量(捕捞量)很多时,价格很便宜。
假设市场投放量等于捕捞量,从(1)获得如下模型 [3] :
(2)
其中,
代表渔船的技术参数或可捕系数,如果
,价格作为常数,则模型(2)可退化为模型(1)。
在(1)中,价格p被看成是常数。(2)中把价格p作为与需求呈正比、与供给呈反比的代数形式来处理。然而在实际的市场经济中,市场需求和市场供给决定了市场的出清价格。这里假设需求曲线是向右下方倾斜的,即
,其中
;供给曲线是向右上方倾斜的,即
,其中
。市场价格时刻受供给量和需求量的影响,当需求量大于供给量时,则价格上升;当供给量大于需求量时,则价格下降。在文献 [2] 中有如下关系:
(3)
结合供给曲线和需求曲线,公式(3)变成
(4)
进而得到如下新的动态价格下的捕捞模型:
(5)
这里龚帕兹规律刻画生物种群增长。其中,系数r代表种群内生增长率,k代表环境的最大承载量(或饱和水平),即代表着栖息地可以容纳的最大种群数量。
本文首先计算出(5)的平衡点并且证明是正的和局部稳定的。其次讨论了(5)渔业的动力学行为,分析和比较在常数价格和均衡价格下生物种群数量和捕捞努力量的变化。最后,给出结论。
2. 平衡点及其稳定性分析
从(5)中第三个方程式可以得到
。由于消费者在边际效用达到最大时(即消费第一单位的某种商品)所愿意支付的最高价格一定大于行业在边际成本达到最小时(即生产第一单位的某种商品)所愿意销售的价格,如果不然,则就不会有买卖发生。因此需求曲线的截距比供给曲线的截距大,即
。又因为
,
,因此
,即均衡价格是正解。
定理2.1:假设
,
,
,那么模型(5)有且仅有一个正均衡点。
证明:由
可解得:
其中,
,
,
把解出来的
代入第二个方程式,解出来
,因为捕捞努力量的单位成本w和技术先进程度参数
都是大于0的,因此
,即均衡存量水平(equilibrium stock size)是正的。
最后把解出来的
代入公式(2),解出来
,因为
必然小于环境最大容纳量k,种群的内生增长率r大于0,因此
,即均衡捕捞努力量是正的。
定理2.2:定理1.1的条件成立,那么均衡点
的局部渐近稳定性。
证明:模型(5)的雅克比矩阵为
在平衡点
处相应的特征方程为:
这里
其中,
,因为
故而
,又加上r大于0,因此
。因为
均大于0且
因此
。
因为
均是大于0的,因此
。由赫尔维茨准则(Routh-Hurwitz criterion)知方程的根均具有负实部,局部渐近稳定。
3. 开放渔业的动力学行为
首先考虑捕捞努力量均衡时,表示为垂直线
。当生物种群数量s小于
时,则有
,即利润为负的,进而有渔民的退出,捕捞努力量入减少。当生物种群数量s大于
时,则有
,即利润为正的,进而有渔民的进入,捕捞努力量增加。
接下来考虑生物种群数量均衡时,表示为曲线
。在均衡线的上方,意味着捕捞努力量E大于
,说明捕捞大于自然增长则生物种群数量降低。在均衡线的下方,意味着捕捞努力量E小于
,说明捕捞小于自然增长则生物种群数量增加。
画出捕捞努力量均衡线和生物种群数量均衡线如图1。
分析后得出在四个象限内生物种群、捕捞努力量的增减性如表1。
在非均衡点处,生物种群数量、捕捞努力量是如何随时间变化的呢?随时间变化的路径与初值有关。为了说明,选择初始的生物种群数量、捕捞努力量在I象限内。
用Matlab绘制均衡价格下和常数价格下趋近于均衡点路径图如图2和图3。
从图2和图3可以看出,在初始的生物种群数量水平上,有利润产生,则会有渔民的进入导致捕捞努力量的增加。在捕捞努力量增加的同时将会减少生物种群的数量。捕捞努力量继续增加直至穿过均衡垂直线进入II象限内。在IIA象限内,捕捞仍然大于自然增长,因此种群数量继续降低。另一方面,利润是负的则会有渔民的退出导致捕捞努力量的减少。捕捞努力量的减少穿过曲线进入III象限内。在III象限内,利润依然是负的,因此捕捞努力量继续减少。捕捞努力量的减少减低了捕捞导致生物种群数量的增加,则穿过了垂直线进入IV象限内。利润开始为正的,则有渔民的进入,捕捞努力量增加。另一方面,捕捞小于自然增长,因此生物种群数量增加。重新进入I象限内,进行着不断循环直至达到均衡点处。
在均衡价格下和常数价格下,两者都可以循环达到均衡点处。但在常数价格下比均衡价格下的均衡状态时生物种群数量
少、捕捞努力量
多。在政府干预价格的情况下,需要谨慎处理价格对生物种群数量和捕捞努力量的影响,可能会造成生物种群的灭绝或者资源没有达到有效配置。
4. 小结
在生物种群捕捞问题上,该生物的市场价格并不是任意常数,而是由市场经济的内部调节控制更符

Table 1. Increasing or decreasing of population and effort in four quadrants
表1. 四个象限内生物种群数量、捕捞努力量的增减性
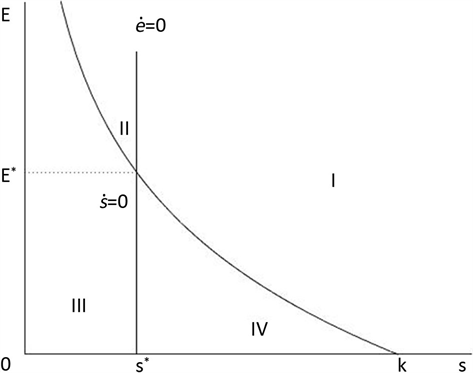
Figure 1. Equilibrium of population and equilibrium of effort divide the area into four quadrants
图1. 由生物种群数量均衡、捕捞努力量均衡分割成四个象限

Figure 2. Derived from model (5), the trajectory of the system over time in equilibrium price
图2. 来源于模型(5),均衡价格下趋近于均衡点的路径图
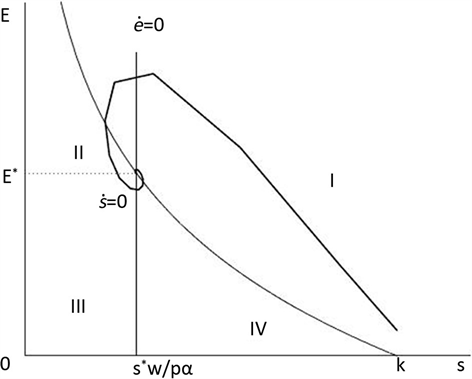
Figure 3. Derived from model (1), the trajectory of the system over time in constant price
图3. 来源于模型(1),常数价格下趋近于均衡点的路径图
合实际生活。从本文中明显可以看出,生物种群数量、捕捞努力量和价格三者在不受外来干扰的前提下会达到一个正的均衡状态且是稳定的。模型(1)中常数价格和模型(5)均衡价格进行对比,得出在常数价格大于均衡价格时,均衡状态时生物种群数量
减少、捕捞努力量
增多的结论。因此,政府部门调控价格时需要谨慎以免造成生物种群灭绝或资源浪费。