1. 引言
洪水是我国最频繁和严重的自然灾害之一。洪水因暴雨形成,具有突发性,破坏性和危险性,可以使村镇、城市及人民生命财产毁于一旦 [1] 。陕北地区洪水灾害严重且频繁,修建水库和堤防等水利工程是必要的防洪措施。而推求设计洪水是防洪规划和建设的依据 [2] [3] 。洪水频率分析法是推求设计洪水的主要途径,在分布函数给定的情况下,参数估计是设计洪水计算的重要工作 [4] 。国内外学者在此方面进行了大量研究,并相继提出了概率权重矩法、权函数法、线性矩法、极大似然法等参数估计方法。实际中,理论频率曲线与实测大洪水点据在大重现期段拟合难以获得满意的结果。为了解决这一问题,国外学者Wang [5] [6] ,Pandey [7] [8] ,Deng [9] [10] 等先后进行了大洪水段的计算研究,主要包括部分概率权重矩(Partial Probability Moments)法,部分线性矩(Partial Linear Moments)法,最小交互熵(Minimum Cross-Entropy)法等。这些方法认为小洪水值在设计洪水估算中具有滋扰行为,可应用截取概率分布进行相对大洪水值的推求。研究结果显示,在大洪水段取得较好的拟合效果,但计算复杂。国内工程设计采用适线法,通过调整参数或给定权重进行经验适线,这些方法适线结果存在一定的主观性和经验性 [11] [12] [13] [14] 。20世纪90年代,高阶线性矩法 [15] (higher-order L-Moments)开始引入洪水分布参数计算,通过提高线性矩阶数来改善大洪水段拟合效果,使外延的大重现期设计洪水值精度得到提高,且借助于计算机,容易实现计算过程。
本文选用陕北地区8个水文站洪峰流量序列为例,以高阶线性矩法进行洪水频率曲线拟合,进而评价所得洪水频率曲线对序列拟合效果及设计值误差。
2. 高阶线性矩
高阶线性矩是高阶概率权重矩 [16] 的线性组合。给定样本容量为n的样本,
表示n个样本点中第i个由小到大的排序值,变量服从
分布。Hosking(1990)提出
的数学期望为
(1)
高阶线性矩定义为
(2)
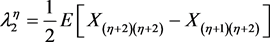 (3)
(3)
(4)
(5)
式中:
表示样本容量为
中最大变量的数学期望,
表示样本容量为
中最大变量的数学期望,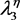 表示样本容量为
中最大变量的数学期望,
表示样本容量为
中最大变量的数学期望。
表示样本容量为
中最大变量的数学期望,
表示样本容量为
中最大变量的数学期望。
当
时,高阶线性矩转化为普通线性矩(Hosking, 1990)。随着
增高,高阶线性矩对随机变量的较大值更为依赖。高阶线性矩的变差系数
,偏态系数
和峰态系数
分别为
(6)
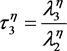 (7)
(7)
(8)
给定一个排序样本
,高阶线性矩的估计量分别为
(9)
(10)
(11)
(12)
(13)
3. 广义极值分布及其高阶线性矩
广义极值分布(Generalized extreme value distribution, GEV)的分布函数为
(14)
其逆函数形式为
(15)
式中:k为形状参数,
为尺度参数,
为位置参数。
当
时,即为Hosking (1985) [17] 给出的GEV分布概率权重矩(PWM)
(16)
把式(14)和式(15)代入式(16),可推出
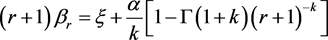 (17)
(17)
当 时,式(14)为EVI型分布(Gumbel分布)。Greenwood (1979) [18] 给出了GEV分布的PWM
时,式(14)为EVI型分布(Gumbel分布)。Greenwood (1979) [18] 给出了GEV分布的PWM
(18)
式中,
为欧拉常数。
将式(17)代入式(1)~式(5),可推出
时,前4阶线性矩分别为
(19)
(20)
(21)
(22)
同样,将式(18)代入式(1)~式(5),可推出k = 0时,前4阶线性矩分别为
(23)
(24)
(25)
(26)
给定一个样本,由式(21),式(20),式(24),式(25)和式(7)可推出
(27)
取k为
,分别令
,计算各阶取值对应的
值,按照(27)拟合曲线,求得式(27)的系数,如表1所示。
应用式(10)和式(11)计算
,根据表1系数,由式(27)计算参数k的估计值
。利用式(20)计算参数
的估计值
(
)为
(28)
由式(19)和式(28)可推出参数
的估计值
(
)为
(29)
4. 实例应用
采用陕西省交口河、张家山、赵石窖、绥德、刘家河等8个水文测站的年最大洪峰资料,经分析,资料满足一致性要求,研究GEV型分布的高阶线性矩法进行洪水序列大洪水段的拟合,资料的基本概况如表2所示。
4.1. 绘制频率曲线
根据表2结果,由式(15)计算洪水设计值,利用期望公式(30)估计经验频率,其表达式为
(30)
式中,P为频率,m为系列样本中的第m项,n为系列样本中的总数。
根据以上计算成果,绘制各站不同阶线性矩的GEV分布理论频率曲线拟合图,详见图1。
根据拟合的频率曲线图,对各站不同阶线性矩法进行比较,分析理论频率曲线与经验点据的拟合情况。由图1可以看出,在P = 0~50%的频率区间,8个测站均随着线性矩阶数的增大,理论频率曲线和经验点据的拟合

Table 1. Coefficients , a 1 , a 2 , a 3 and a 4 for Eq. (27)
表1. 式(27)的拟合系数
,
,
,
和

Table 2. Comparison of quantile errors using different orders L-Moments
表2. 不同阶线性矩法的设计值偏差比较
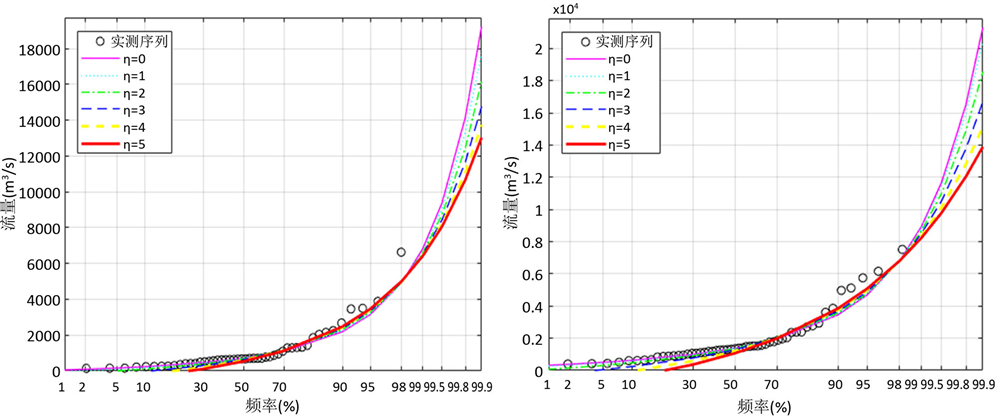 (a) 交口河(b) 张家山
(a) 交口河(b) 张家山  (c) 赵石窖(d) 绥德
(c) 赵石窖(d) 绥德 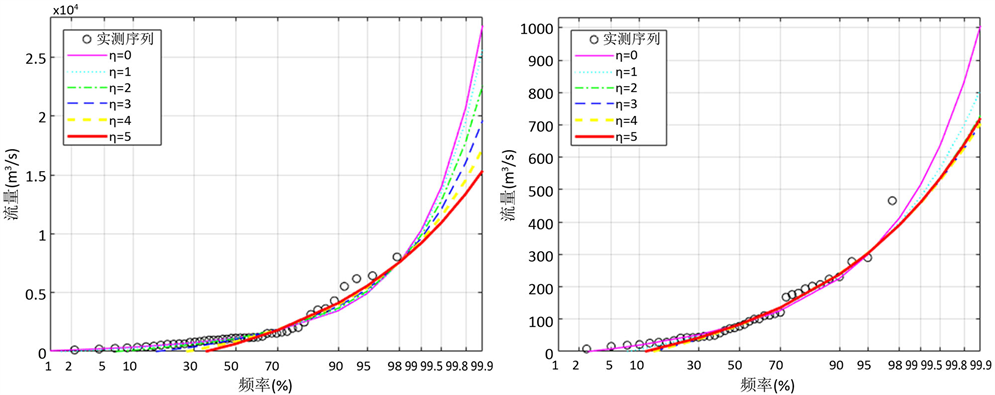 (e) 刘家河(f) 张村译
(e) 刘家河(f) 张村译 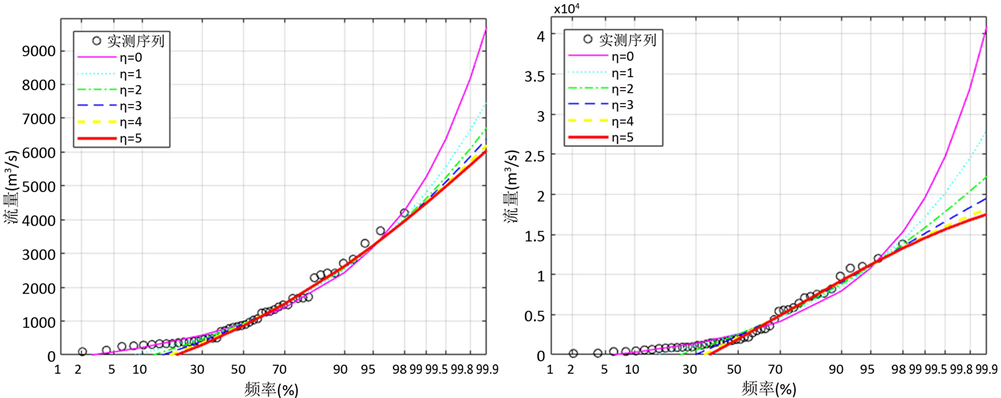 (f) 林家村(g) 神木
(f) 林家村(g) 神木
Figure 1. Fitting of the GEV distribution to annual maximum flows for different orders L-Moments
图1. 年最大洪峰序列各阶线性矩频率曲线拟合图
效果不显著;在P = 50%~99%的频率区间,8个测站均随着线性矩阶数的增大,理论频率曲线和经验点据的拟合效果得到显著改善,说明本方法计算大重现设计洪水值的偏差小。因此,从实测序列值拟合结果可知,采用高阶线性矩法进行拟合计算时,大洪峰段取得较好的拟合效果。
4.2. 拟合效果分析
应用累积相对偏差平方和
分析上述不同阶线性矩法对经验点据的拟合效果。式(31)为P = 50%~98%时,对应实测值与设计值累积偏差平方和的计算公式。
(31)
式中:
为实测值;
为设计值。计算结果如表2所示。
由表2看出,除了张村译站以外,其余7个站点的
均随着线性矩阶数
的升高而减小,即大洪水段实测值与设计值之间的偏差逐渐减小,说明大重现期设计值在阶数较高时与实测值更为接近,这与图1中的拟合结果相一致。而张村驿站,在
时,大洪水段实测值拟合效果与其它7站变化趋势相同,但
时,设计值估算偏差变大,说明并非
越大越好,即并非给与的权重越大越好,而是选择合适的
值,可提高设计值估算精度。所以,通过提高线性矩阶数的方式来拟合序列大洪水段是可行的,可为外延的大重现期设计值提供有利依据。
综合以上分析,在研究区大重现期设计值计算中,建议选用不超过4阶线性矩。
5. 结论
以陕北地区8个水文测站的年最大洪峰流量序列为例,以高阶线性矩法对洪峰序列进行参数估计,评价其拟合效果及设计值的偏差。结果表明,高阶线性矩法通过增大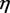 值的方式来拟合大洪水值是可行的,且随着
的增大,大重现期设计值计算偏差越小,可为研究区防洪工程建设提供理论依据。但并非
越大越好,应选择合适的
值,可提高设计值估算精度。但高阶线性矩法还存在一定的问题,由于P-III型分布的逆函数无法表达为显式函数,推导P-III型分布参数与高阶线性矩法的关系式存在较大的困难。因此,在今后的研究中,应重点研究高阶线性矩法在P-III型分布参数估计中的应用研究。
值的方式来拟合大洪水值是可行的,且随着
的增大,大重现期设计值计算偏差越小,可为研究区防洪工程建设提供理论依据。但并非
越大越好,应选择合适的
值,可提高设计值估算精度。但高阶线性矩法还存在一定的问题,由于P-III型分布的逆函数无法表达为显式函数,推导P-III型分布参数与高阶线性矩法的关系式存在较大的困难。因此,在今后的研究中,应重点研究高阶线性矩法在P-III型分布参数估计中的应用研究。