1. 引言
电动汽车(Electric Vehicle, EV)作为一种清洁能源交通工具,可显著减少化石能源使用量,改善大气质量。然而,电动汽车不同于其他用电负荷,其行驶和充放电行为都具有高度的不可预测性 [1] [2] 。并且,当局部配电系统的调度方式及设备容量不能满足电动汽车随机的充电量时,将导致线路电压的严重下降。因此,在电动汽车已成为行业发展趋势的情况下,必须要采取一定的激励及控制策略,引导电动汽车合理参与V2G (Vehicle-to-grid, V2G)服务,避免造成配电网不稳定运行 [3] [4] [5] 。
文献 [6] 分析了不同情景下电动汽车对电压稳定裕度的改变程度,并提出了一种提高系统稳定性的控制策略。文献 [7] [8] [9] 分析通过电价激励方式调控电动汽车实现有序充放电,增加车主收益和降低电网运行成本。文献 [10] [11] [12] 提出了基于市场环境下的电动汽车充电策略。文献 [13] [14] [15] 提出了一种电网为主体的博弈调度策略,构建了使各方利益最大化的非合作博弈模型。文献 [16] 提出了基于代理商管控的博弈策略,为研究电网的需求侧响应开辟了新的角度。文献 [17] [18] [19] 确定响应V2G的电动汽车电池的可用容量,验证其响应电网调峰的有效性。上述文献表明,合理地管控电动汽车的入网规模及引导车主的充放电行为,不但可避免其对电网的稳定运行带来冲击,还可在一定范围内优化电网的负荷曲线、网络损耗。因此,规模化电动汽车入网对系统稳定的评估、控制及优化调度,是十分必要和紧迫的 [20] 。
本文以城市配电网的电动汽车入网调度问题为研究对象,通过蒙特卡洛法计算城网内各时段动力电池可用充放电容量,再利用主从博弈方法决策分时电价,对电动汽车充放电时段加以调控,降低负荷波动。最后,利用PSASP平台,对比不同规模和电池响应率的电动汽车有序入网对电压稳定性的改善程度,验证了本文构建的采用主从博弈及分时电价引导的电动汽车充放电模型控制效果。
2. 静态电压稳定性
2.1. 充放电负荷
电动汽车的充放电行为影响参数众多,充放电时刻、日行驶里程、电池容量、电池响应率等参数都会改变每辆电动汽车的充放电功率值。其中,私家车的充放电情况更是与个人行驶习惯相关,更加难以调控。针对上述影响因素,本文根据每时段电动汽车停驶率统计数据,判定电动汽车入网的充放电时段分布特性,并利用蒙特卡洛方法,抽取一定概率分布下电动汽车日行驶里程值来估算行驶用电量和剩余可用容量,计算出处于不同水平的电池响应率下电动汽车每时段及一天内的充放电功率值。模型简化处理当电动汽车处于停驶状态时,则会迅速接入电网充放电。图1为某城市电动汽车每时段的停驶率统计情况。
从图1中可以看出,各时段电动汽车的停驶率均大于90%,这为电动汽车支持V2G服务容量提供了较大空间。
电动汽车的日行驶里程反映了电动汽车的耗电量水平,虽然个体车辆具有随机性,但规模化的汽车行驶里程总体分布仍符合一定的概率密度函数:
(1)
式中,参数
;
;x表示当前的日行驶里程值。
电动汽车荷电状态SOC值表示动力电池此时所剩容量占总容量的比例。在充满电状态下,定义SOC = 100%。此外,考虑到电动汽车随时具有行驶需求,应设定一个初始状态值,避免动力电池过低电量时响应V2G服务,本文设置SOC0 = 20%。基于上述设定,每时段的荷电状态值:
(2)

Figure 1. The stopping rate of electric vehicles at each time
图1. 电动汽车每时段的停驶率分布
式中,d表示实时行驶里程值;
表示最大行驶里程值。
2.2. 电压稳定裕度
本文以New England的10机39节点系统模拟某一城市区域电网。基准功率为100 MVA,基准电压为345 kV,系统网络结构如图2所示。母线9为电动汽车公共接入点。
在分析域网内电压稳定情况时,基于PSASP进行潮流计算,不断进行小干扰电压稳定计算,得到系统负荷变化时的PV曲线,进而可得到每个电动汽车负荷下的稳定极限。定义电网的电压稳定裕度为:
(3)
式中,
表示各时段电动汽车功率极限点的负荷增长率。
3. 主从博弈模型
3.1. 博弈模型及目标函数
在本文采用的博弈模型中,将电网视作博弈主体,电动汽车车主视作博弈从体,一天24 h作为一个调度周期。主从博弈过程如图3所示。
博弈主体作为领导者,先行制定分时电价(决策
),从而引导博弈从体改变其电动汽车充放电行为(决策
)。在决策执行过程中,博弈主体将根据从体的决策执行情况进行决策调整,做出更加有利于自身利益的决策(
),从体策略随之改变(
)。如此反复,主从双方不断博弈调整,直至策略集
达到主从博弈的均衡点,即博弈双方的利益最大化。
设博弈主体的目标函数是电网负荷均方差,定义如下。
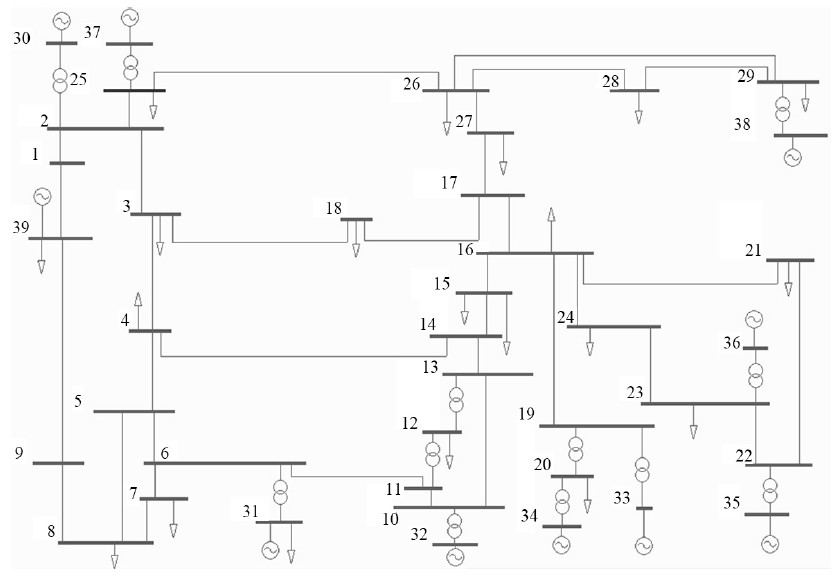
Figure 2. Simulation network system one-line diagram
图2. 仿真网络系统单线图

Figure 3. Flowchart of Stackelberg game process
图3. 主从博弈流程图
(4)
(5)
式中,
表示域网内负荷均方差;
表示t时段的原始负荷功率;
表示t时段电动汽车的充放电功率,且设放电功率数值为负;
表示一天内域网负荷平均值。
电动汽车车主以充放电策略响应电网的调度需求,通过分时电价的充放电价差,使其在电动汽车电池寿命损耗等使用成本之外获得收益。设车主净收益为博弈从体的目标函数。
(6)
(7)
式中,
表示一天内车主的净收益;
表示电网在t时段的电价;
表示电池损耗的补偿价格,其值为负;
表示放电时电网决策的补偿电价。
3.2. 约束条件
在电网和电动汽车车主的博弈中,还会受到各种约束条件的限制。其中,电网设计分时电价作为先行决策,在峰荷期提高电价,低谷期降低电价,并根据电动汽车车主的反馈程度,不断优化电价策略,保证电网一天内的售电总收益不变的情况下,利用充放电价差提高车主收益。博弈主体定义分时电价约束条件如下:
(8)
(9)
式中,
表示电网售电总收益;
表示峰段电价;
表示平段电价;
表示谷段电价。
电动汽车响应V2G时,必须保证其行驶需求。此外,还需考虑电池损耗成本,不能无限制进行充放电。基于上述要求,电动汽车充放电总功率最大应满足条件为:
(10)
(11)
式中,
表示t时段的放电功率;
表示一天内的最大放电总功率;
表示t时段的充电功率;
表示一天内的充电总功率,一般情况下,其值为常数,数值与行驶用电量相关。
此外,由于城市范围内电动汽车每时段的充放电功率值主要受电动汽车规模及其行驶习惯的影响,存在一定的最大可调度容量。因此,每时段都必须为电动汽车充放电功率设定上下限值,定义如下:
(12)
式中,
表示在t时段能接入电网的最大规模量;
、
表示每时段平均最大充放电功率。
3.3. 求解算法
对博弈模型的求解可分为内、外两部分。内层求解得到电动汽车响应分时电价的调度策略回应集,外层求解则为了进一步优化分时电价,取得最优分时电价决策。
在内层求解中,电网先行制定分时电价,电动汽车考虑各种约束条件后跟随做出最佳调度策略集,以求得到最大利益。设定电网决策
的策略集合
,电动汽车决策
的策略集合
,优化目标为
,并给与一定松弛度
,目标函数为:
(13)
在外层求解中,电网以最小回应集对
中最不利于
的策略做出响应,寻找最优分时电价
,优化目标为
。其目标函数为:
(14)
在双方充分博弈后,选取电动汽车策略集合
中最满足
的策略
作为纳什均衡点,使
成为满足博弈双方利益最大化的策略集合,即满足:
(15)
4. 算例
为了验证本文建立的主从博弈模型及负荷调度策略的优越性,本文基于图2供电网络,并依照某地区实际日负荷特性,构建了一个包含电动汽车负荷的区域电网算例模型。按照人口面积配比,区域内电动汽车数量确定为500、1000辆两个规模。其中,每辆电动汽车均采取慢充模式,充放电效率取100%,电池容量24 kWh,最大充放电功率4 kW,初始荷电状态(SOC)为20%。此外,动力电池响应率考虑50%和90%两种模式。
V2G模式下,不同规模及响应率电动汽车入网,负荷曲线变化情况如图4所示。
图4中数据表明,一天内,12:00电网负荷最高,6:00电网负荷最低。电动汽车若峰荷期10:00~18:00接入电网充当储能装置反向放电,低谷期1:00~8:00合理充电,可大幅降低负荷峰谷差率;并且,伴随电动汽车规模或电池响应率的增大,负荷的调节效果更好。表1对比了各模式下电网负荷曲线的改善程度。
此外,基于PSASP平台对算例模型进行潮流分析和小干扰电压稳定计算,得到如图5所示的各时段电压稳定裕度。
图5中数据表明,一天内,12:00系统负荷裕度最高,6:00系统负荷裕度最低。电动汽车在1:00~8:00的负荷低谷期增大负荷,此时电压稳定裕度适度减小,不会对电网稳定造成冲击;在10:00~18:00的峰荷
期接入放电,则可增大电压稳定裕度,避免负荷快速增长引起电压失稳,提高了运行的稳定性。表2对比了各种调度情况下电压稳定裕度标准差率及改善情况。
表2数据表明,随着接入汽车数量及响应率的增加,电压稳定裕度曲线越平稳,这对于提高系统运行稳定性具有积极意义。

Figure 4. Load curves of power grid under different V2G modes
图4. 不同V2G模式下的负荷曲线

Figure 5. Voltage stability margin of power grid under different V2G modes
图5. 不同V2G模式下电压稳定裕度对比

Table 1. Comparison of load characteristics of electric vehicles
表1. 电动汽车对负荷特性的优化对比

Table 2. Comparison of voltage stability of electric vehicle
表2. 电动汽车对电压稳定的优化对比

Table 3. Time-of-use price before and after the game
表3. 博弈前后的分时电价

Table 4. Car owner’s income under different V2G modes
表4. 不同模式下的车主收益
本文算例中,经过充分博弈,优化分时电价及车主收益情况的对比如表3、表4所示。
从表3可以看出,优化后的峰价段和平价段电价增大,谷价段电价减小,并且电动汽车数量和响应率越大,电价变化幅度越大。这种变化趋势更利于电动汽车车主响应电网的负荷调度策略。表4中数据表明,电动汽车的V2G模式运行为车主带来了收益,且电动汽车数量和响应率越大,其净收益越大。
5. 结语
为抑制电动汽车无序入网带来的负荷波动和电压稳定问题,本文提出了一种基于电网/车主主从博弈模式的分时电价调整策略,并借此调整电动汽车车主的充放电时段。并考虑汽车数量及电池响应率等参数,分析了不同V2G模式下的电网负荷波动、电压稳定裕度及车主收益变化,得到如下几点主要结论。
1) 电动汽车响应V2G策略入网有利于负荷平抑与电压稳定性的提高。在可用电池容量低于3%最大负荷容量的情况下,电动汽车的有序充放电可使负荷峰谷差率降低12.15%,电压稳定裕度的标准差提高24.7%。
2) 主从博弈模型适用于电动汽车参与V2G的分时电价决策问题。执行电网与电动汽车车主充分博弈后的分时电价,能够实现在电网售电收益不变的前提下,显著提升电动车主的综合收益。
3) 随着电动汽车规模以及电池响应率的增加,谷段电价的降低以及峰段、平段电价的提高,更有利于电网负荷曲线的平抑、电压稳定裕度的提高以及车主收益的增加。