摘 要
本文选取1997~2016年云南省人均GDP、第三产业占GDP比重和衡量环境污染程度的各项指标,构建有关经济增长、产业结构、环境污染的VAR模型。结论表明:1) 经济增长、产业结构与度量环境污染的程度的各项指标存在协整关系。2) “倒U型”环境的库兹涅茨曲线是否成立依赖于所选地区的数据和所选取的环境污染指标的不同。3) 经济增长在环境污染度量指标的波动中占主体地位。4) 云南省现有的环境污染问题会抑制经济的增长,且伴随经济增长所产生的环境问题主要是工业废气的排放。
关键词 :VAR模型,环境库兹涅茨曲线,经济增长,产业结构,环境污染

Copyright © 2018 by author and Hans Publishers Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


1. 引言
最近,中国经济的可持续增长备受世人瞩目。环境资源具有不可替代性,众多研究表明,中国在经济高速增长的同时付出了沉重的环境代价,此外经济的高速增长会影响环境变化。产业结构决定了区域内经济增长的质量,同时也是节能减排的主要抓手,通过调整产业结构,可以改变经济发展方式,实现提质增效。在未来的经济发展中,如何处理经济增长、产业结构、环境污染三者之间的内在关联,就成为了一个比较急迫而实际的问题。在这种过程中,找到某种平衡路径的前提条件是要对经济增长、产业结构和环境污染的关系进行深入而具体的研究。从当前学者有关研究来看,国内对于这一方面的研究有待提升。从20世纪90年代中期开始,云南省进入经济发展快速发展时期,随着GDP的增加,环境污染、资源大量消耗、生态系统的退化等问题使得云南省经济发展与环境之间关系越来越尖锐。高消耗、高排放、低产出、低收入的现状并未得到实质性的改变,云南省为经济发展所付出的代价依然很高。云南省在产业结构和环境污染方面比较具有代表性。故本文基于对云南省1997~2016年的云南省经济增长、产业结构和环境污染构建VAR模型。通过研究云南省经济增长、产业结构以及环境污染之间动态关系,寻找地方经济增长、产业结构和环境污染之间的关系,为云南省政府提供一些关于发展可持续经济的政策建议。
2. 文献综述
美国经济学家Grossman (1991)等在研究中首次指出,人均GDP与环境污染排放指标(SO2和烟尘的排放量)之间存在着“倒U型”曲线的关系 [1] 。Grossman和Kreuger (1995)对多个国家环境污染排放物的研究表明:多数国家的人均国民收入和环境污染的变动之间呈“倒U型”曲线关系,结论表明:人均国民收入位于4000~5000美元时,对于环境的污染最大。这样刻画的经济增长和环境污染与之间的关系和Kuznets所提出的收入不均和经济增长之间的关系相似,所以将其称作“环境的库兹涅茨曲线(Environmental Kuznets Curve,简称EKC)” [2] 。众多学者对是否存在EKC曲线展开了大量的研究,例如Selden and Song [3] 和Galeottia and Lanza [4] 等认为EKC曲线存在。Egli在2002年对德国的环境数据进行了分析,否认了EKC曲线的存在 [5] 。
国内学者对于经济增长、产业结构和环境污染之间关系的研究可作以下分类:1) 关于经济增长和环境污染间关系的研究。马树才(2006)等在对国内的环境数据进行了实证分析,得出的结论否认了“倒U型”的环境库兹涅茨曲线的存在 [6] 。张晓(1999)根据1985~1995年的中国数据,建立了时间序列,经分析我国的人均GDP与环境污染水平(废气排放量和SO2排放量)之间呈比较不明显的“倒U型”弱环境库兹涅茨曲线特征 [7] 。郑长德和刘帅利用空间计量的方法系统分析了各省份在空间上的环境污染问题,发现环境污染较大的省份也是经济发达地区,认为在短时期实现环境治理难度较大 [8] 。包群等(2005)对1996~2002年中国面板数据进行考察,认为估计方法以及污染指标的选取是影响倒U型曲线的重要因素 [9] 。盖美等利用弹性分析法和SFA、Tobit回归研究了辽宁沿海经济带环境问题与经济增长之间的关系 [10] 。2) 关于产业结构与环境污染之间的研究。徐成龙等用LMDI方法,论证了山东省1994 2010年产业结构变化对环境产生的影响 [11] 。仲伟周等通过横纵两个维度研究我国产业结构与环境之间的关系 [12] 。3) 关于经济增长、产业结构和环境污染之间的研究。于峰、齐建国等(2006)在Stern (2002)模型的基础上,通过研究我国28个省(市、区) 1999~2004年的SO2排放量及其表征,发现环境污染与产业结构和能源结构变动、经济规模扩大正相关,与环保技术创新、生产率提高负相关,并估算了各自对环境的贡献率 [12] 。黄少博通过双重差分模型研究了省际之间环境污染对经济增长和产业结构的影响 [13] 。
国内学者对经济增长、产业结构和环境污染关系的研究主要有两种路径:首先对其方法的研究;其次是划分区域深入研究。从方法的研究方面来看,绝大多数的计量模型采用最小二乘法即OLS方法进行估计,解释变量间可能会存在多重共线性的问题,会带来参数显著性水平不可信的困境。从区域化的研究方面来看,学者们大多做的跨国分析以及地域分析,缺乏从某个省份这种角度对中国经济增长,产业结构和环境污染之间的具体而全面研究分析。但是,由于不同的国家有关区域经济发展和环境质量和模式不尽相同。所以,能否得出“倒U型”的库兹涅茨曲线取决于地区的数据和评价环境污染所选取的指标。本文基于对云南省1997 2016年的云南省经济增长、产业结构和环境污染的VAR模型,通过研究云南省经济增长、产业结构以及环境污染之间动态关系,寻找地方经济增长、产业结构和环境污染损失之间的关系,为云南省政府对于发展可持续经济提供一些可行性的政策建议。
3. 云南省经济增长、产业结构和环境污染的现状分析
云南省地处我国西南的边陲,自然环境优美,近二十年以来经济稳步发展。2016年全省完成生产总值14,869.95亿元,同比增长8.7%。人均GDP由1997年的4121元,经过近20年的稳步增长,截止到2016年增加为30,949元(如图1)。从产业结构上看(如图2),从1997~2016年,第一产业比重逐年呈下降趋势,第二产业占GDP比重在1997~2010年较为稳定,位于40%左右,至2010以后成下降趋势。第三产业占GDP比重呈现上升趋势。云南省至2013年前产业结构的分布与国家一样,三次产业呈“二、三、一”结构分布。从图2中可知至2013年后的云南省产业结构三次产业结构由“二、三、一”到“三、二、一”产业结构转型升级初步完成,即以旅游业为代表的第三产业在产业结构中起主导作用。云南省2016年第一产业总值为2195.04亿元,较2015年增长5.6%,占云南省GDP比例为14.8%;第二产业总值为5799.34亿元,较2015年增长8.9%,占云南省GDP的比例为39.0%;第三产业总值为6875.57亿元,较2015年增长9.5%占云南省GDP的比例为39.0%。2016年云南三次产业结构比例依次为14.8:39.0:46.2,

Figure 1. Yunnan province per capita GDP timing chart
图1. 云南省人均GDP时序图
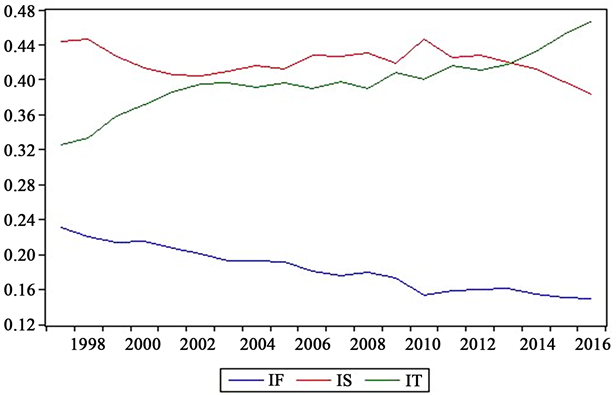 注:IF表示第一产业占比、IS表示第二产业占比、IT表示第三产业占比
注:IF表示第一产业占比、IS表示第二产业占比、IT表示第三产业占比
Figure 2. Yunnan province industrial structure trend chart
图2. 云南省产业结构趋势图
相较于2015年的15.1:39.8:45.1有所优化,第三产业占GDP比重同比增长1.1%。总的来说云南省从2013年开始,从以第二产业为主导到第三产业为主导的产业结构转型初步形成。
云南省的经济快速增长的同时环境污染问题应当引起重视。1997年工业固体废物的排放量是433.4万吨,2016年减少为1.52万吨(如图3)。较之1997减小了285倍。从工业废物结构上看,工业二氧化硫排放量(如图4)由1997年的41.1万吨增加到2016年的52.62万吨,2016年是1997年的1.28倍,其中2010~2012年为增长最为迅速的时间段,增幅达15.9%,但在从2012年后成下降趋势。
4. 模型方法及数据处理
(一) VAR模型
VAR模型即向量自回归模型,在1980年由Sims第一次提出。VAR模型的特点是用将所有当期变量作为因变量,所有变量的若干滞后作为解释变量进行回归。VAR的模型主要用于预测随机干扰项对于
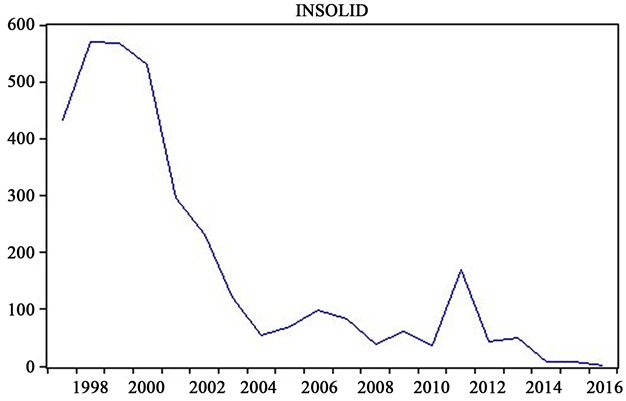
Figure 3. Trend chart of total industrial solid waste emission in Yunnan province
图3. 云南省工业固体废物排放总量趋势图
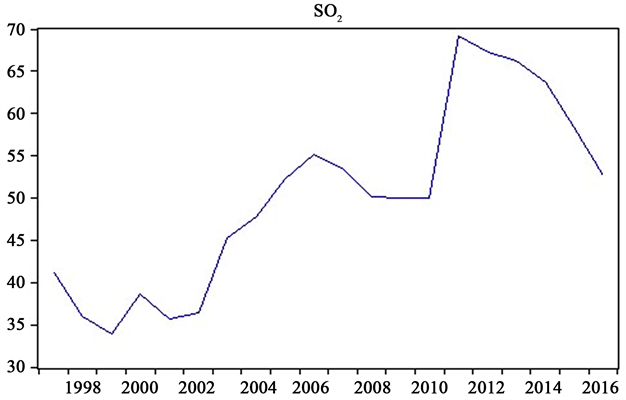
Figure 4. Sulfur dioxide emission trend chart of Yunnan province
图4. 云南省二氧化硫排放量趋势图
所研究变量的动态冲击,冲击大小、正负和持续时间和将VAR模型中制定变量的方差分解到每个干扰项上,提供每个干扰项所引起的VAR模型所引起的系统内各个变量的相对程度 [14] 。
VAR定义式为
是
阶时间序应变量列向量,则p阶VAR模型(记为VAR(p)):
(1.1)
式中,
是第i个待估参数的
阶矩阵
可以同期相关,但通常不与自己的滞后值相关,也不与等式右边的变量相关;
为
阶方差协方差矩阵;
P为滞后阶数。
由(1.1)式可知,VAR(p)模型是以N个第t期变量
为应变量,以N个应变量
的最大p阶滞后变量为解释变量的方程组模型,方程组模型中共有N个方程。显然,VAR模型是单变量AR模型推广到多变量组成的“向量”自回归模型。
对于两个变量(N = 2),
时,VAR(2)模型为:
用矩阵表示为:
待估参数个数为
。
用线性方程组表示VAR(2)模型:
(二) 滞后阶数选择
VAR模型中最佳滞后阶数即p值越小,残差有可能存在自相关的问题,所带来的后果是参数估计不具有一致性。增加p值可消除残差中自相关问题。然而p值不能太大,p值太大,待估参数变多,所带来不利影响是自由度严重降低,直接影响参数估计的有效性。在这里介绍常用的两种选择p值的方法 [14] 。
1) 用SC和AIC准则确定最佳滞后期数,即p值。P值的选取方法为,在p值增大过程中同时使AIC和SC的值最小。
2) 用LR(似然比统计量)选择最佳的p值,其中
。
其中,ln(p)和ln(p + i)分别为VAR (p)和VAR (p + i)的对数形式的最大似然值,
表示自由度。
(三) 指标和数据的选取
本文选取的是1997~2016年有关经济增长、产业结构、环境污染的时间序列数据。具体而言,经济增长数据采用云南省的人均GDP,产业结构数据采用第三产业占GDP比重,环境污染方面采用工业废水排放量、二氧化硫排放量。其中将所有数据对数化处理(见表1),以便消除可能存在的异方差性进而获得平稳的时间序列。本文的所有数据均取自《云南省2017年统计年鉴》。
5. 实证分析
首先对各时间序列进行单位根检验,避免因非平稳数据造成的伪回归;然后进行Granger因果检验;在确定最佳滞后阶数,建立VAR模型;最后依次进行VAR平稳性检验,协整检验、脉冲响应分析和方差分解分析。
(一) 单位根检验
时间序列的平稳性检验有多种方法,包括DF检验、ADF单位根检验、PP单位根检验等。本文选择常用的PP单位根检验,滞后阶数根据SIC、SC准则确定。由表2可知,在5%的显著性水平下,lnagdp、lnit、lnSO2、lninwater、lninsolid不平稳;一阶差分后,四类时间序列数据拒绝有单位根的原假设表现为平稳,即lnagdp、lnit、lnislnSO2、lninwater均是一阶单整。
(二) 确定最佳滞后阶数
滞后阶数确定及VAR模型建立。除了各时间序列数据需要满足一定的平稳性条件外,最优滞后阶数的确定亦是VAR模型构建的重要组成部分。根据Eviews 8.0软件提供的滞后阶数判定标准得到相关结果。由表3可知,AIC和SC选择不同的滞后阶数,则检验LR统计量如下:
故拒绝原假设选择VAR(2)。
此时VAR(2)模型能够反映云南省经济增长、产业结构、环境污染之间的关系,表达式如下:
(三) VAR平稳性检验
再确定了最佳滞后阶数后还应进行VAR平稳性检验避免后面脉冲响应分析和方差分解分析没有意义。判断标准为VAR方程的特征根在单位圆内部检验结果如表4和图5所示。
(四) Johansen协整检验
由PP检验可知,lnagdp、lnit、lninwater、lnSO2都是1阶单整,是变量具有协整关系的前提,下面将根据Johansen协整检验判断经济增长、产业结构和度量环境污染的指标之间的协整关系如表5所示。
注:检验模式(c, t, k)中,c代表截距项;t代表趋势项;k代表滞后项;0代表示没有该项。

Table 3. Delayed order decision results
表3. 滞后阶数判定结果
注:*表示判定结果。

Table 4. Characteristic root distribution table
表4. 特征根分布表
No root lies outside the unit circle. VAR satisfies the stability condition.

Table 5. Co-integration test results of lnagdp, lnit, lninwater and lnSO2
表5. lnagdp、lnit、lninwater、lnSO2协整检验结果
注:*表示在5%显著性水平下拒绝原假设。
由表5协整检验结果可知至少存在三个协整向量说明lnagdp、lnit、lninwater、lnSO2存在协整关系。
(五) Granger因果检验
Johansen协整检验显示lnagdp、lnit、lninwater、lnSO2存在协整关系,然而这4个变量之间是否存在相互关系却不得而知,所以要对以上四个时间序列进行Granger因果检验,结果如表6所示。
由表6可知在5%的显著性水平下人均GDP是产业结构、环境污染的格兰杰原因,反之则不然。将显著性水平放宽到10%可知产业结构和环境污染存在单向的格兰杰因果关系即环境污染是产业结构的格兰杰原因,但是产业结构不是环境污染的格兰杰原因。
(六) 基于VAR模型的响应脉冲分析
由VAR平稳性检验可知特征根在单位圆内故VAR(2)是平稳的,由此可知所构建的VAR模型是有效的。所以可在VAR模型估计的基础上,使用脉冲响应分析人均GDP和环境污染的各项指标之间的冲击响应,刻画每个变量之间动态的变化关系。所得到脉冲响应图,如图6~图8所示,其中,横轴为滞后阶数;纵轴为施加冲击后变量变化率;蓝色的曲线表示脉冲响应函数,表示受其他变量随机干扰项一个标准差的冲击后所研究变量在现在和未来之间持续的变化率。两边的红色虚线为±2倍标准差偏离带。本文选取的脉冲响应模型滞后期数为20期。
如图6所示,在当期给产业结构一个标准差的冲击后,会对云南省经济增长产生负面效应,并在第6年达到最小值,随后第7年到第17年递增,从第18年开始递减直至第20年趋近与0。初期,云南省的产业结构主要是以第二产业为主,但慢慢地随着以旅游为主导的第三产业的兴起,云南省的经济呈现一定程度的繁荣。因此产业结构迫切需要新一轮产业结构调整。给工业废水排放一个冲击后,经济增长受到了负向的影响,在第5年达到最小值后开始递增,到第20年趋于零,这与工业废水排放量的“倒U型”的环境库兹涅茨曲线不符。生产规模增加会产生更多的工业废水,从治理的角度的来看处理废水的代价要高于经济增长的速度,但随着时间的推移这种负反馈会越来越小,大量的废弃物的排放会给经济增长带来负面影响。给SO2排放量一个冲击后,经济增长受到了正向影响,在第8年达到最大值后开始下降,到第20年趋近于0。这种显现先上升后下降的变化趋势表明了云南省的经济增长与环境污染呈现一定“倒U型”的环境库兹涅茨曲线,总的来说“倒U型”环境的库兹涅茨曲线是否成立依赖于所选地区的数据和所选取的环境污染指标的不同。云南省旅游业的兴起带来相应的工业生产规模增加会产生更多的SO2的排放,从而在短期内提高经济产出,由于超过规模效应最佳值,大量的SO2排放会给经济增长带来负面影响。此阶段若加大环境治理力度,倡导绿色旅游,则可将不利影响转化成促进经济增长的积极因素。
从图7可知,给经济增长一个冲击后,初期会对云南省的产业结构产生不利的影响,但随着时间的变化这种不利的影响逐渐降低,到第12年人均GDP的增长达到最大,随后至第20年降至0附近。即从
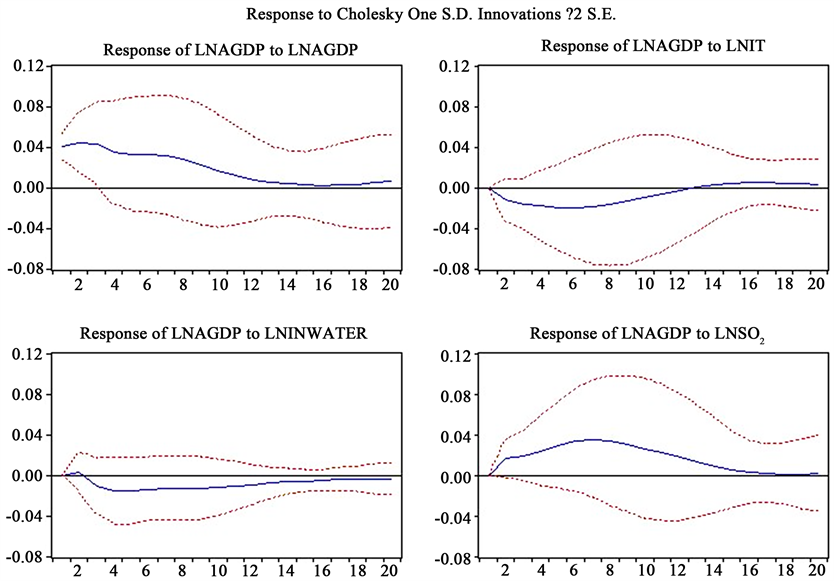
Figure 6. Lnagdp impulse response analysis of lnagdp, lnit, lninwater and lnSO2
图6. lnagdp对lnagdp、lnit、lninwater和lnSO2的脉冲响应分析
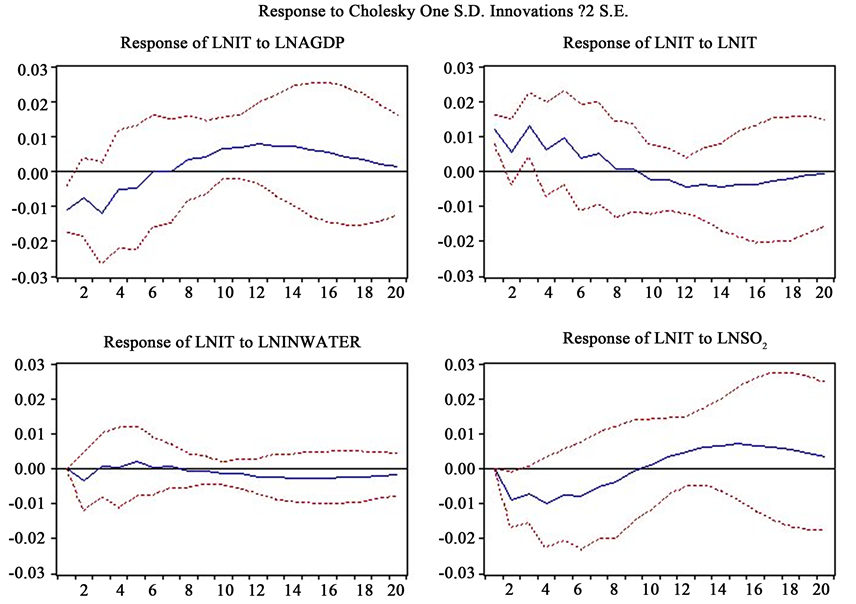
Figure 7. lnit impulse response analysis of lnagdp, lnit, lninwater and lnSO2
图7. lnit对lnagdp、lnit、lninwater和lnSO2的脉冲响应分析
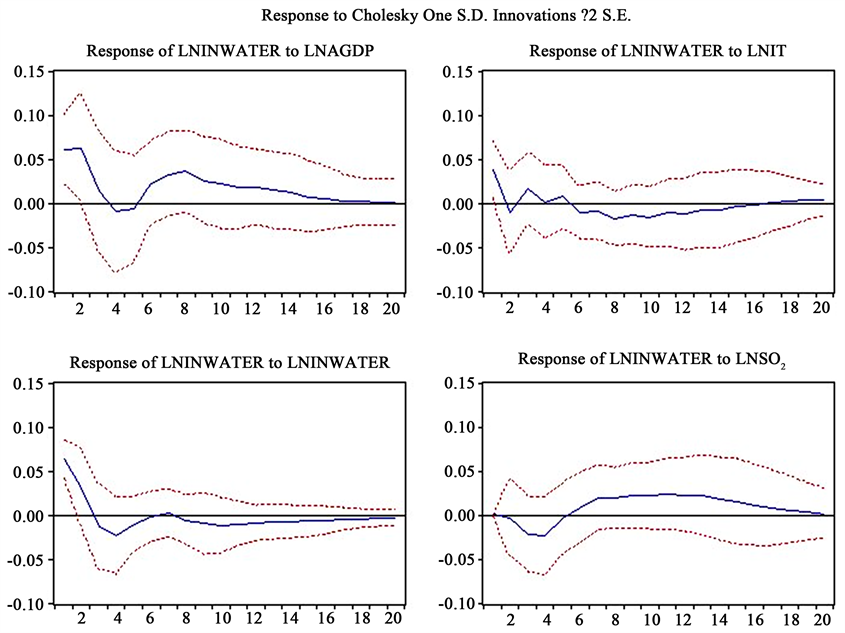
Figure 8. Pulse response analysis of lninwater to lnagdp, lnit, lninwater and lnSO2
图8. lninwater对lnagdp、lnit、lninwater和lnSO2的脉冲响应分析

Table 6. Granger causality test
表6. Granger因果检验
长期来看,经济增长对产业结构会产生负向影响,但随着产业结构的转型,这种不利的情况得以缓解。本文用第三产业与生产总值的比重代表产业结构系数,从产业结构对经济增长冲击响应效果分析可知,经济增长对第三产业的依赖较强,但这种趋势也符合云南省实际发展情况。2013年之前,第三产业比重始终处于增长状况但低于第二产业的比重;2013年,以旅游业为代表的第三产业占GDP的比重赶超第二产业成为促进云南省经济增长的新动力;在2013年后由“二三一”到“三二一”产业结构升级已经初步形成,符合产业结构转型升级的规律。给工业废水排放量和SO2排放排放量一个冲击后,产业结构受到微弱的负向影响,并在第5年达到峰值,之后在0附近波动,且SO2排放量波动幅度大于工业废水排放的幅度。环境污染增的加剧在初期会引起第三产业规模的小幅度的下降随后第三产业呈正向增长,即会在短期内抑制第三产业占比,但在产业结构转型升级的大背景下,由于以旅游为特色的第三产业崛起,一定会挤占第二产业占比的上升趋势。
从图8和图9可知,给经济增长一个冲击后,负向影响工业废水排放量和SO2排放量,到第4年达到最大,随后有一定上升趋势随后至第20年逐渐衰减到0.即初期工业废水排放量和SO2排放量与经济增长有一定关联,随后关联越来越弱。同样,对产业结构施加一个冲击,工业废水排放量和SO2排放量受到的影响几乎与横轴平行,即受到的影响十分微弱,此结果符合格兰杰因果检验中的结论。即产业结构往往具有很强的惰性,很难在短时间内发生太大的调整,因此它对工业废水排放量和SO2排放量的冲击是长期延续的,且随着时间迁移这种影响会越来越弱。
(七) 基于VAR模型的方差分解分析
一般来说,与脉冲响应分析不同的是,方差分解分析可以将VAR模型系统内一个变量的方差分解到每个个扰动项上,并提供每个扰动因素影响VAR模型内各个变量的相对程度 [14] 。将时间区间(1997 2016年)作为滞后期,在VAR (2)结果的基础上,分别对经济增长、产业结构和对度量环境污染的指标进行方差分解。
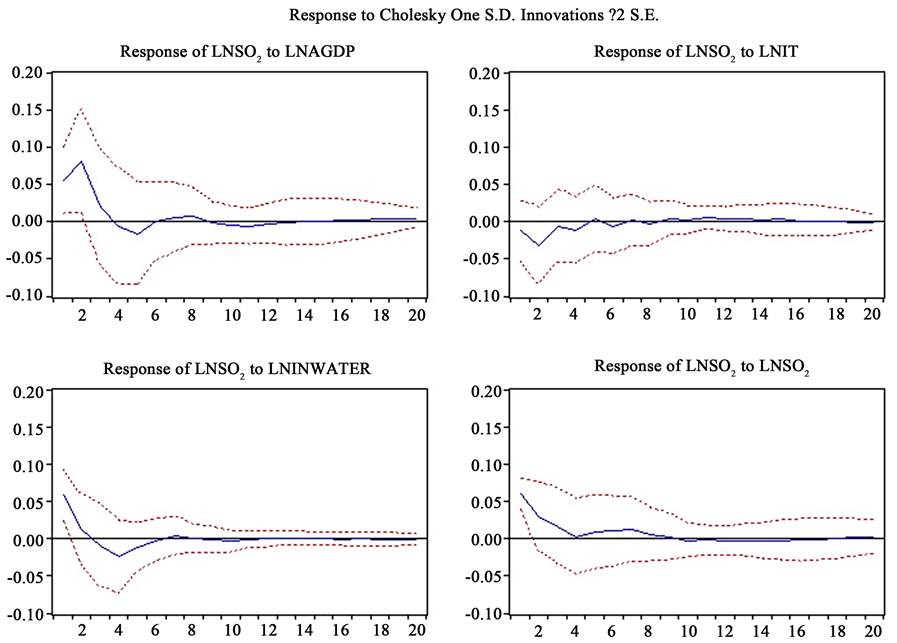
Figure 9. Pulse response analysis of lnSO2 to lnagdp, lnit, lninwater and lnSO2
图9. lnSO2对lnagdp、lnit、lninwater和lnSO2的脉冲响应分析
由图10结合方差分析图可知,经济增长由其自身解释的占比迅速下降,由第1期的100%滑落至第20期的50%,从第10期开始,下降速度放缓,第10到第20期变化不明显。产业结构在8期之前对经济增长的解释呈现正向增长的趋势,并在第8期达到峰值为11.24%,随后稍有回落随后逐渐趋于平缓,对经济的增长解释维持在10%左右。经济增长由SO2排放量解释程度在第11期前保持上升趋势,随后增长较为缓慢,在第25期后,成为经济增长波动最主要的解释部分。总体上看,前9期经济增长自身解释占主体;第10期至第24期,则是产业结构;经济增长由工业废水排放量解释占比排在最末。结合云南省实际的经济运行状况,在1997~2016年,云南省产业结构还处在“二三一”向“三二一”结构转型的阶段,虽然第二产业对于云南省经济贡献较大,但从2013年开始以旅游业为特色的第三产业在经济增长的作用超过了第二产业。在这样的大环境下,云南省经济增长更多的依靠第三产业推动,第三产业不景气,则会影响云南省的经济发展。随着2013年之后的“三二一”产业结构转型升级,第三产业的地位得到提升显著提高,云南省经济发展将迎来新一轮的上涨。
由图11结合方差分析图可知,在产业结构的波动中,由本身的解释程度逐渐下降,在第20期维持
在28%左右。经济增长的解释呈先下降,在上升再下降的波动的形式在第20期维持在32.15%。SO2的解释占比则不断攀升,最后稳定在30%左右,说明在产业结构的波动中,SO2的排放起到了主导地位,这也表明两者的格兰杰因果关系。工业废水的排放量的解释占比维持在3%左右,说明工业废水在产业结构变动中作用不大。但是工业废气却对云南省产业结构转型有着较大的影响,推动着云南省经济加速从“二三一”到“三二一”产业结构的转型,经济增长对产业结构的变化只是作为长期的基础性的作用。
图12和图13可知,在工业污水的排放和SO2排放的波动中的波动中,其经济增长占据了主导地位,始终维持在40%~50%之间,而产业结构的波动维持在10%左右的水平。这是因为第二产业是所有行业环境污染源的主体,环境污染的指标对产业结构变化十分敏感。而第三产业对环境污染远不及第二产业,
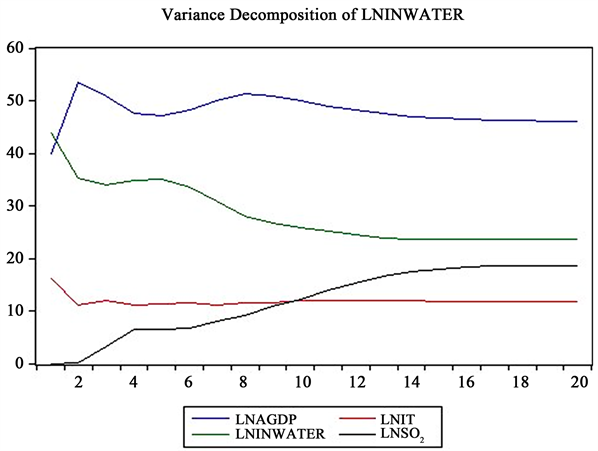
Figure 12. Variance decomposition of lninwater
图12. lninwater的方差分解分析
第三产业对于经济增长的贡献从2013年开始超过第二产业。所以加快云南省产业结构从“二三一”到“三二一”的转变刻不容缓。这与云南省发展绿色经济有直接关系,单位GDP所带能来的环境污染逐年下降,经济增长与环境污染正加速实现脱离。
6. 结论政策建议
(一) 结论
本文在VAR计量模型基础之上,利用格兰杰因果检验、协整检验、脉冲响应分析和方差分解对1997~2016年云南省经济增长、产业结构和环境污染程度的各项指标的动态关系进行了实证研究,从而得出以下结论:1) 经济增长对产业结构和度量环境污染的各项指标的单项格兰杰因果表明环境污染的加剧不一定会带来经济增长,环境污染的程度水平主要取决于产业结构特征。2) 经济增长和环境污染的“倒U型”库兹涅茨曲线是否成立取决于地区的数据和环境污染所选取的指标的不同。3) 在云南省的经济增长、产业结构和环境污染的动态关系研究中发现,随着云南省经济增长产生的主要环境问题是SO2的大量排放,工业废水排放量相对较少。4) SO2的排放在产业结构波动中逐渐超过产业结构对本身的解释程度,成为主要的解释方面。5) 产业结构在经济增长波动的解释中有上升的趋势,经济增长在环境污染度量指标的波动中占主体地位,大量工业生产带来各种环境问题,SO2和工业废水、排放量不断增多,抑制着云南省经济的发展。所以加快云南省产业结构从“二三一”到“三二一”的转型升级变得十分重要。
(二) 政策建议
1) 改变传统的发展观念,加快绿色环保的先进技术的发展 [15] 。从长期来看,环境污染会对经济增长带来不利的影响,在环境污染和经济发展之间矛盾日益明显的今天,致力于绿色、低污染的经济发展能够有效的克服这种不利影响。所以贯彻环境治理的理念和加快由粗放向集约型发展到提高资源利用效率、加快可持续发展变得刻不容缓。
2) 加快产业结构转型升级。云南省的第三产业至2013年开始超过第二产业所占比重,第二产业能源消耗大所产生的废物较多,在环境污染占主要解释部分。而相对大力发展第三产业对于环境的污染一般较低。云南省已经初步实现了“三二一”产业结构的转型升级,以2016年为例,三次产业占比分别为14.91%、38.38%、46.71%,第三产业比第二产业多8.33%。当前,云南省以旅游业、金融保险业、房地产业为代表的现代服务业正蓬勃发展,这类行业均属于低污染高附加值的第三产业,对于实现低污染,高产出、实现三次产业结构合理配置起到重要的推动作用。
3) 大力发展先进制造业。在进行产业结构升级转型的过程中也不能忽视第二产业中的贡献,第二产业是所有行业造成环境污染最为严重的部分。目前,云南省工业行业中烟草工业冶金、建材供需矛盾突出,高能耗高污染的粗放集约式的发展已不能适应云南省的经济发展。在“中国制造2025”的环境下,云南省应当大力发展先进的生产技术把握时代契机,升级传统工业,优先发展新能源、新材料等一批新兴产业,为云南省经济可持续发展注入新的动力。
4) 提高信息公开透明度,加大普通群众参与度 [16] 。普通民众是环境污染的直接受害者,民众对于处理环境污染的热情较高。民众参与的一个重要前提是信息公开透明。信息不公开,民众无法有效的对政府污染处理工作进行监督。有些地方政府对于环境污染治理的信息不能及时的公开、信息不对称。所以,政府应当提高信息公开透明度,加大普通群众参与度,让民众能够清楚云南省重大环境污染事件,亦或告知群众普通常态数据,让民众参与其中提高环保意识。
5) 强化环保法律的惩罚制度,环境的污染程度越高对于普通民众的伤害也越大,产生这些污染源的企业公司往往注重自身利益的最大化而忽略这些生产的外部性对于普通民众的影响,所以云南省政府应当加大对于企业污染不处理的惩罚力度,让他们认识到不能只关心眼前利益应该立足于长远发展,从而在一个绿色而和谐的环境中共同促进云南省经济可持续发展。