高阶非线性减振系统的主动控制的研究

Study on the Active Control of Vertical Nonlinear Suspension System

摘要: 列车减振系统可简化成单自由度振动模型，在这个模型中考虑五次非线性刚度因素，采用时滞阻尼器来控制其竖向振动。采用多尺度法分析，得出系统的理论近似解，研究非线性刚度系数、阻尼系数、反馈增益系数和时滞量等因素对竖向振动的减振效果，并分析其规律，为工程应用中的减振项目提供理论指导。

Abstract: The vehicle suspension system can be simplified into a single-degree-of-freedom vibration model. Five nonlinear stiffness factors are considered in this model, and a time-delay damper is used to control its vertical vibration. Using multi-scale analysis, the theoretical approximate solution of the system is obtained. The effects of nonlinear stiffness coefficient, damping coefficient, feedback gain coefficient and time delay on vertical vibration reduction are studied, and the regularity is analyzed, which can provide theoretical guidance for vibration reduction projects in engineering applications.

1. 引言

列车运行过程中有很多振动形式，竖向振动是其振动的主要方式之一。竖向振动也会影响乘坐列车的体验 [1] [2] 。之前对列车减振系统的研究一般会简化成线性模型进行分析 [3] [4] [5] ；但是所有的列车减振系统基本上都存在非线性特性 [6] [7] [8] 。随着非线性振动理论的发展，越来越多的学者开始研究列车减振系统的非线性特性 [9] [10] 。特别是近年来，对列车竖向非线性减振系统的研究越来越多，这属于典型的非线性系统案例。为了更加精确地减振系统，本文考虑列车的五阶非线性刚度，分析在这种情况下非线性刚度系数、阻尼系数、反馈增益系数和时滞量等因素对竖向振动的减振效果，并分析其规律，为工程应用中的减振项目提供理论指导。

2. 力学模型

本文研究的单自由度的列车减振系统模型有质量块、非线性弹簧、和时滞半主动阻尼器组成。采用的是时滞反馈减振技术，如图1所示，减振体系的运动方程为：

$m\ddot{x}\left(t\right)+kx\left(t\right)+\delta x^5\left(t\right)+c\stackrel{\dot{}}{x}\left(t\right)+f_{sc}\ddot{x}\left(t-\tau \right)=F_0\cos \left(wt\right)$ (1)

式中，m表示质量块的质量，k是线性弹簧的刚度系数， $\delta$ 是非线性弹簧的刚度系数，力和位移之间的关系为 $F_k=kx+\delta x^5$ ，系统所承受外激励可简化为 $f\left(t\right)=F_0\cos \left(wt\right)$ ，时滞反馈力为， $f_{sc}$ 为时滞反馈系数， $\tau$ 是时滞量。

Figure 1. Illustration of model

图1. 模型图

3. 摄动分析

首先进行求导换元：

$\frac{\text{d}x}{\text{d}t}=\frac{w{x}_c}{\Omega }\cdot \frac{\text{d}y}{\text{d}T}$ ， $\frac{{\text{d}}^{2}x}{\text{d}{t}^2}=\frac{w^2{x}_c}{{\Omega }^2}\cdot \frac{{\text{d}}^{2}y}{{\text{d}}^{2}T}$ ， $\frac{{\text{d}}^{2}x\left(t-\tau \right)}{\text{d}{t}^2}=\frac{w^2{x}_c}{{\Omega }^2}\cdot \frac{{\text{d}}^{2}y\left(T-{\tau }_c\right)}{\text{d}{T}^2}$ (2)

其中 $\Omega$ 为无量纲频率 [3] 。

对(1)式进行的系统变量进行无量纲化处理，令：

$y=\frac{x}{x_c}$ ， $T=\frac{w}{\Omega }t$ ， ${\tau }_c=\frac{w}{\Omega }\tau$ ， $w_0=\sqrt{\frac{k{\Omega }^2}{m{w}^2}}$ ， ${\xi }_1=\frac{\delta x_c^4{\Omega }^2}{m{w}^2}$ ， ${\xi }_2=\frac{c\Omega }{mw}$ ， $f_s=\frac{f_{sc}}{m_c}$ ， $F=\frac{F_0{\Omega }^2}{m{x}_c{w}^2}$ (3)

将式(2)和式(3)代入式(1)，可以得出以下无量纲方程：

$\ddot{y}\left(T\right)+w_0^{2}y\left(T\right)+{\xi }_1{y}^5\left(T\right)+{\xi }_2\stackrel{\dot{}}{y}\left(T\right)+f_s\ddot{y}\left(T-{\tau }_c\right)=F\cos \left(\Omega T\right)$ (4)

为了便于分析，将系统变量进行重新标定，其中 $0<\epsilon \le 1$ ：

${\xi }_1=\epsilon {\hat{\xi }}_1$ ， ${\xi }_2=\epsilon {\hat{\xi }}_2$ ， $f_s=\epsilon {\hat{f}}_s$ ， $F=\epsilon \hat{f}$ ， $\tau ={\tau }_c=\hat{\tau }$ ， $y_{\tau }=y\left(T-\hat{\tau }\right)$ ， $\Omega =w_0+\epsilon \sigma$

将上式代入(4)式，可得如下方程：

$\ddot{y}\left(T\right)+w_0^{2}y\left(T\right)=\epsilon \left[-{\hat{\xi }}_1{y}^5\left(T\right)-{\hat{\xi }}_2\stackrel{\dot{}}{y}\left(T\right)-{\hat{f}}_s{\stackrel{\dot{}}{y}}_{\hat{\tau }}+\hat{f}\cos \left(\Omega T\right)\right]$ (5)

根据泰勒展开式，方程(5)的解可近似表示为：

$y\left(T,\epsilon \right)=y_0\left(T_0,T_1\right)+\epsilon y_1\left(T_0,T_1\right)$ ， $y_{\hat{\tau }}\left(T,\epsilon \right)=y_{0\hat{\tau }}\left(T_0,T_1\right)+\epsilon y_{1\hat{\tau }}\left(T_0,T_1\right)$ (6)

根据多尺度法将式(6)代入式(5)，比较 $\epsilon$ 的零次幂和一次幂可得：

${\epsilon }^0:D_0^2{y}_0+{\omega }_0^2{y}_0=0$ (7)

${\epsilon }^1:D_0^2{y}_1+w_0^2{y}_1=-2D_0{D}_1{y}_0+\left[-{\hat{\xi }}_1{y}_0^5-{\hat{\xi }}_2{D}_0{y}_0-{\hat{f}}_s{\stackrel{\dot{}}{y}}_{0\hat{\tau }}+\hat{f}\cos \left(w_0{T}_0+\sigma T_1\right)\right]$ (8)

式(7)的通解可以表示为：

$y_0=a\left(T_1\right)\cos \left[w_0{T}_0+\phi \left(T_1\right)\right]=A\left(T_1\right){\text{e}}^{i{w}_0{T}_0}+cc$ (9)

其中： $A\left(T_1\right)=\frac{a\left(T_1\right)}{2}{\text{e}}^{i\phi \left(T_1\right)}$ ，cc代表其前面各项的共轭，后不赘述。

外激励项和时滞项可以表示成如下的复数形式：

$\hat{f}\cos \left(w_0{T}_0+\sigma T_1\right)=\frac{1}{2}\hat{f}{\text{e}}^{i\left(w_0{T}_0+\sigma T_1\right)}+cc$ (10)

$y_{0\tau }=A_{\tau }\left(T_1\right){\text{e}}^{i{w}_0\left(T_0-\tau \right)}+cc$ (11)

在假设 $\tau$ 和 $\epsilon$ 都很小的前提下， $A_{\tau }$ 可以按照泰勒级数展开为如下的形式

$A_{\tau }=A\left(T_1\right)-\epsilon \tau A^{\prime }\left(T_1\right)+\frac{{\left(\epsilon \tau \right)}^2}{2}{A}^{″}\left(T_1\right)+\cdots$ (12)

将(9)~(12)式代入到式(8)中，可以得到：

$$ (13)

由此可得式(13)的可解性条件：

$-i2w_0{D}_{1}A-10{\hat{\xi }}_1{A}^3{\bar{A}}^2-i{w}_0{\hat{\xi }}_{2}A-i{w}_0{\hat{f}}_{s}A{\text{e}}^{-i{w}_0\hat{\tau }}+\frac{\hat{f}}{2}{\text{e}}^{i\sigma T_1}=0$ (14)

将代入(14)

$-i{w}_0{D}_{1}a+a{w}_0{D}_1\phi -\frac{5}{16}{\hat{\xi }}_1{a}^5-i{w}_0{\hat{\xi }}_2\frac{a}{2}-i{w}_0{\hat{f}}_s\frac{a}{2}{\text{e}}^{-i{w}_0\hat{\tau }}+\frac{\hat{f}}{2}{\text{e}}^{i\left(\sigma T_1-\phi \right)}=0$ (15)

分离实部和虚部可得：

$D_{1}a=-\frac{a}{2}{\hat{\xi }}_2-{\hat{f}}_s\frac{a}{2}\cos \left(w_0\hat{\tau }\right)+\frac{\hat{f}}{2w_0}\sin \left(\sigma T_1-\phi \right)$ (16)

$a{D}_1\phi =\frac{5}{16w_0}{\hat{\xi }}_1{a}^5+{\hat{f}}_s\frac{a}{2}\sin \left(w_0\tau \right)-\frac{\hat{f}}{2w_0}\cos \left(\sigma T_1-\phi \right)$ (17)

令 $\varphi =\sigma T_1-\phi$ ，则上式为：

$$ (18)

$a\sigma -a{D}_1\varphi =\frac{5}{16w_0}{\hat{\xi }}_1{a}^5+{\hat{f}}_s\frac{a}{2}\sin \left(w_0\hat{\tau }\right)-\frac{\hat{f}}{2w_0}\cos \varphi$ (19)

对于稳态的主共振响应，令上两式中的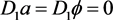，得到与振幅和相位满足的代数方程组：

$\frac{\hat{f}}{2}\sin \varphi =\frac{a}{2}{w}_0{\hat{\xi }}_2+{\hat{f}}_s{w}_0\frac{a}{2}\cos \left(w_0\hat{\tau }\right)$ (20)

$\frac{\hat{f}}{2}\cos \varphi =\frac{5}{16}{\hat{\xi }}_1{a}^5+{\hat{f}}_s{w}_0\frac{a}{2}\sin \left(w_0\hat{\tau }\right)-a\sigma w_0$ (21)

两式平方相加可得：

$\frac{{\hat{f}}^2}{4}={\left[\frac{a}{2}{w}_0{\hat{\xi }}_2+{\hat{f}}_s{w}_0\frac{a}{2}\cos \left(w_0\hat{\tau }\right)\right]}^2+{\left[\frac{5}{16}{\hat{\xi }}_1{a}^5+{\hat{f}}_s{w}_0\frac{a}{2}\sin \left(w_0\hat{\tau }\right)-a\sigma w_0\right]}^2$ (22)

两边同时乘以 $4{\epsilon }^2$ ，且将 $\Omega =w_0+\epsilon \sigma$ 代入可得到与、 $\tau$ 、a相关的无量纲方程：

(23)

4. 系统参数对减振性能的影响

本文主要研究非线性刚度系数 ${\xi }_1$ 、阻尼系数 ${\xi }_2$ 、反馈增益系数 $f_{sc}$ 和时滞量 $\tau$ 对系统的减振效果，并研究其规律。

当反馈增益系数 $f_{sc}$ 和时滞量 $\tau$ 都为零时对应被动减振系统。式(23)变为：

$F^2={\left[a{w}_0{\xi }_2\right]}^2+{\left[\frac{5}{8}{\xi }_1{a}^5-2a{w}_0\Omega +2a{w}_0^2\right]}^2$ (24)

选取参数 $w_0=1.75,F=0.2$ ，当阻尼系数 ${\xi }_2$ 不变时取 ${\xi }_2=0.1$ ，改变系统的非线性刚度系数 ${\xi }_1$ ，可以得到图2，从图2可以得出，非线性因子会使振幅峰值发生偏离，非线性刚度系数 ${\xi }_1$ 越大，共振峰值

Figure 2. Stiffness versus amplitude

图2. 刚度与振幅

频率向右偏移越多，同时同一频率所对应的峰值出现了多值情况，系统会出现跳跃现象，不利于结构的稳定。当非线性刚度系数 ${\xi }_1$ 不变时取 ${\xi }_1=0.5$ ，改变系统的阻尼系数 ${\xi }_2$ ，可以得出图3，从图3可以得出，阻尼可以使振幅减小，阻尼越大，振幅越小，但是当阻尼增大到一定程度时，阻尼的增大的减振效果不是很明显。

当反馈增益系数 $f_s$ 和时滞量 $\tau$ 都不为零时对应主动减振系统，对应的频响函数为式(23)，选取参数 ${\xi }_1=0.4,{\xi }_2=0.1,F=0.2,w_0=1.75,\Omega =1.6$ ，当反馈增益系数 $f_s$ 不变时，分别取 $f_s=0.75,1,1.6$ ，可得图4，从图4可以看出，振幅随时滞量呈周期性变化，在振幅的最大处出现跳跃现象。当时滞量不变时，分别取 $\tau =0.5,1,1.5$ ，可得图5，从图5可以看出， $f_s=-0.3$ 左右，系统的振幅达到最大，因此在该种情况下要避免选择反馈增益系数在 $f_s=-0.3$ 附近工作。

5. 系统的稳定性与分岔

对于稳态的主共振响应，令， $a{D}_1\varphi =f_2\left(a,\varphi \right)$ ，则设：

$S_1=\frac{\partial f_1}{\partial a}=-\frac{{\hat{\xi }}_2}{2}-\frac{{\hat{f}}_s}{2}\cos \left(w_0\hat{\tau }\right)$ ， $S_2=\frac{\partial f_1}{\partial \varphi }=\frac{\hat{f}}{2w_0}\cos \varphi =\frac{5}{16w_0}{\hat{\xi }}_1{a}^5+{\hat{f}}_s\frac{a}{2}\sin \left(w_0\hat{\tau }\right)-a\sigma$

$S_3=\frac{\partial f_2}{\partial a}=\frac{1}{a}\left[\sigma -\frac{25}{16w_0}{\hat{\xi }}_1{a}^4-{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)\right]$ ， $S_4=\frac{\partial f_2}{\partial \varphi }=\frac{\hat{f}}{2w_0}\sin \varphi =-\frac{1}{2}{\hat{\xi }}_2-{\hat{f}}_s\frac{1}{2}\cos \left(w_0\hat{\tau }\right)$

$cr=\left[\frac{5}{16w_0}{\hat{\xi }}_1{a}^4+{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)-\sigma \right]\left[\sigma -\frac{25}{16w_0}{\hat{\xi }}_1{a}^4-{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)\right]$

微分方程(18)、(19)的Frechet导数为： $\text{Frechet}=\left[\begin{array}{cc}{S}_1& S_2\\ S_3& S_4\end{array}\right]$ ，其特征矩阵为：

$\det \left[\begin{array}{cc}{S}_1-\lambda & S_2\\ S_3& S_4-\lambda \end{array}\right]=0$ (25)

Figure 3. Damping versus amplitude

图3. 阻尼与振幅

Figure 4. Time delay versus amplitude

图4. 时滞与振幅

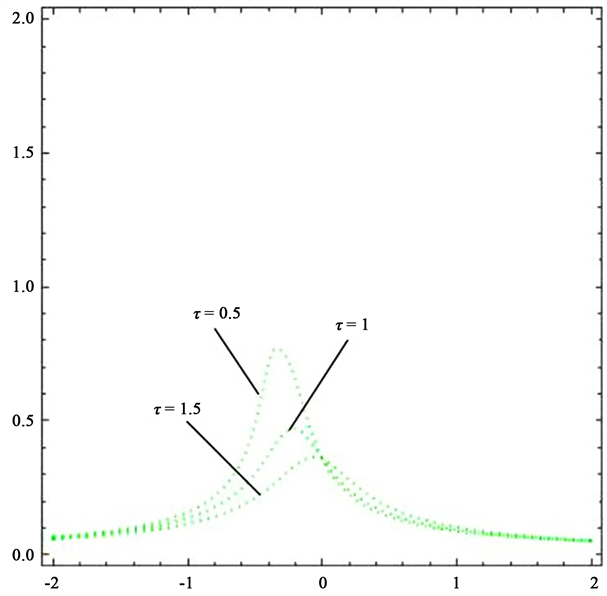
Figure 5. Feedback gain versus amplitude

图5. 反馈增益与振幅

其特征方程为 ${\lambda }^2+\left[{\hat{\xi }}_2+{\hat{f}}_s\cos \left(w_0\hat{\tau }\right)\right]\lambda +S_1{S}_4-S_2{S}_3=0$ ，根据罗斯准则，系统稳定的充分必要条件是：

$B=\left[{\hat{\xi }}_2+{\hat{f}}_s\cos \left(w_0\hat{\tau }\right)\right]>0$

$A={\left[\frac{{\hat{\xi }}_2}{2}+\frac{{\hat{f}}_s}{2}\cos \left(w_0\hat{\tau }\right)\right]}^2-\left[\frac{5}{16w_0}{\hat{\xi }}_1{a}^4+{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)-\sigma \right]\left[\sigma -\frac{25}{16w_0}{\hat{\xi }}_1{a}^4-{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)\right]>0$

将相应的参数代入后，如果 ${\hat{\xi }}_2+{\hat{f}}_s\cos \left(w_0\hat{\tau }\right)>0$ 不总成立说明存在不稳定的解，因此调节时滞和反馈增益系数时，可能会发现跳跃现象，破坏系统的稳定性；如果 ${\left[\frac{{\hat{\xi }}_2}{2}+\frac{{\hat{f}}_s}{2}\cos \left(w_0\hat{\tau }\right)\right]}^2-\left[\frac{5}{16w_0}{\hat{\xi }}_1{a}^4+{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)-\sigma \right]\left[\sigma -\frac{25}{16w_0}{\hat{\xi }}_1{a}^4-{\hat{f}}_s\frac{1}{2}\sin \left(w_0\hat{\tau }\right)\right]<0$ 系统的响应可能会无限发散，最终导致结构破坏。

选取参数 ${\xi }_1=0.4,{\xi }_2=0.1,F=0.2,w_0=1.75,f_s=1,\tau =0.8$ ，将稳定性方程、被动减振方程、时滞减振方程的函数曲线图放到一个坐标系下，如图6，分析其稳定性

根据图6可知，区域1包含在区域2内，为不稳定区域，被动减振方程和时滞减振方程均处于稳定区域。在时滞的作用下，共振点向右移动，时滞振动曲线的峰值降低，这说明时滞起到了很好的减振作用。

6. 结论

非线性刚度会使振幅峰值发生偏移，系统出现跳跃现象，但对减振没有很大的帮助，因此尽可能地选择线性弹簧或者非线性刚度小的弹簧作为减振器的部件；阻尼可以使振幅减小，但是到一定程度时，

Figure 6. Stability domain versus oscillating curve

图6. 稳定区域与振动曲线

阻尼的减振效果不是很明显，因此在实际中要结合经济因素和使用要求来选择合适的阻尼材料；时滞量随外激励的频率呈周期性变化，表明时滞在部分区间对减振有促进效果，部分区间使振动恶化，在振幅的最大处还出现跳跃现象，因此在实际工程应用中，要选择合理的时滞量来减小系统的振动，避免系统振动的跳跃失稳；反馈增益系数在某个固定值及其附近减振效果最差，因此要合理的选择反馈增益系数，避免阻尼减振器的反馈增益系数在这个值附近起作用。

基金项目

本论文受到以下基金的资助：国家自然科学基金资助项目(11372125)，江西省自然科学基金资助项目(20161BAB101005)，航空科学基金资助项目(2017ZA56001)。

参考文献

NOTES

^*通讯作者。