1. 引言
超深亚微米SOI MOSFETs器件因其抗闩锁、高速、低功耗、抗辐照等优良特性,在低压、低功耗电路、耐高温电路、微机械传感器、光电集成、无线通讯等方面都有重要应用。随机掺杂波动(Random Dopant Fluctuation, RDF)是粒子热扩散等造成的一种本征现象。对于短沟道器件,其沟道内杂质原子总数较少,因此杂质数目相对涨落将达到较大的比值。且由于注入、扩散等工艺的随机性,沟道内粒子的位置的分布同样是随机的。随机分布造成器件参数失配,引起漏致势垒降低对器件参数产生很大影响 [1] [2] [3] 。随着工艺技术的进步,器件特征尺寸逐步缩小,沟道掺杂粒子的随机掺杂引起阈值电压的剧烈波动,严重影响电路的性能。
源漏RDF通过影响器件的沟道电势和接触电阻对FD-SOI晶体管的阈值电压的波动等统计特性具有重要影响 [4] 。随机波动掺杂对SOI MOSFETs的抗电离总剂量辐照能力有重要影响,这种影响主要体现在期间被辐照之后。总剂量辐照和随机掺杂剂波动的综合效应已在45 nm部分耗尽SOI器件中得到了验证 [5] 。通过在器件的沟道中引入一定的掺杂波动,模拟现实中的RDF现象。发现RDF影响SOI器件的截止频率同时建立了关段电流和截止频率的解析模型 [6] 。RDF的波动包括,掺杂粒子数目和粒子位置波动两种。仿真模拟表明,RDF的波动对器件的阈值电压等关键参数的波动影响较大 [7] ,但是仿真结果只能表明特定情况下的结论,并不能预测不同情况下参数的波动。更重要的是,将粒子数目和位置的波动混合在一起,不能直观的了解两种波动的比值,不利于对器件的理解。Y. Yasuda巧妙的将这两种效应进行了独立分析和整体研究,并且发现数目的波动与位置的波动成一定比值。这个比值与器件的沟道掺杂浓度、沟道长度等之间相关 [8] 。这类模型的仿真,只能定性的告诉我们器件特性的波动与器件参数的关系,同时仿真需要很多的计算资源,提出了一个粗略的解析模型来分析SOI器件沟道掺杂数目波动引起的阈值电压的波动 [9] 。本文在充分调研已有模型的基础上,提出一种由沟道粒子数目波动引起的阈值电压波动标准差的解析模型,建立了反应沟道粒子数目波动和位置变化的阈值电压模型,该模型将为控制超深亚微米SOI MOSFETs器件阈值电压波动提供重要的理论预测。
2. 短沟道SOI MOSFETs阈值电压模型
对于短沟道SOI MOSFETs器件,可采用如图1所示的高斯箱法求解器件沟道区泊松方程来得到器件阈值电压 [10] 。
二维泊松方程如下:
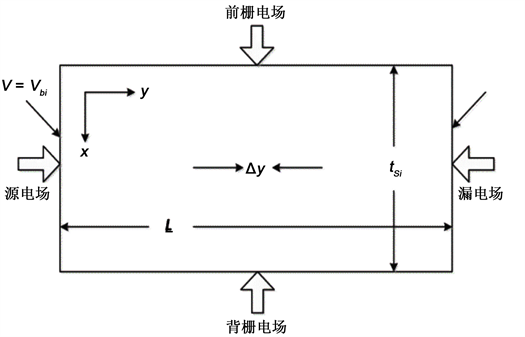
Figure 1. Gaussian box method for solving threshold voltage
图1. 高斯箱法求解阈值电压示意图
(1)
上式中
代表整个高斯箱内的电势分布,NA代表高斯箱内即器件沟道的掺杂浓度,q代表元电荷,
代表硅的介电常数。在硅膜内进项准二维求解,假定埋氧化层电场均匀分布,可将方程(1)化简为
(2)
η1可以看作工艺常数,通过拟合得到。通过拟合参数η1来说明横向电场Esf(y)/η1的影响。tsi为硅膜区厚度,Vfbf、Vfbb分别为沟道正、背表面的平带电压。Cox、Csi、Cbox分别代表栅氧、硅膜和埋氧等效电容。
根据高斯定理及SOI MOSFETs器件正背栅耦合效应,可以求得阈值电压表达式如下:
(3)
其中,Vth,L为长沟器件阈值电压,∆Vth为短沟道器件电压漂移量示 [10] 。
(4)
(5)
(6)
(7)
(8)
3. 反应沟道粒子数目波动和位置变化的阈值电压标准差模型
沟道RDF引起的阈值电压的波动
可以表示成数目波动
和波动
两种主要效应共同作用的结果,它们之间关系可由式(9)描述。
(9)
3.1. 粒子数目波动引起的阈值电压波动
将器件正、背栅的平带电压,沟道表面强反型时的表面势等代入式(4),到长沟道FD SOI器件的阈值电压的表达式
(10)
假设沟道内粒子数目的波动符合泊松分布,粒子数目主要集中在理想掺杂浓度附近。对于在式(10)中出现的关于浓度的函数,可利用泰勒公式进行一阶近似来拟合粒子数目的波动。式(10)可化为
(11)
(12)
(13)
(14)
(15)
式中,
表示器件沟道掺杂的理想浓度,是式(8)中自然对数函数进行泰勒展开的基点。器件正表面修正的金属功函数、正表面修正的电子亲和能、硅的能带宽度以及背栅的等效平带电压不受沟道内杂质浓度的影响,即B1代表了不受杂质浓度波动影响的物理量。
短沟道器件阈值电压还有修正项,对修正项采用相同的处理方法,可最终得到短沟道器件的阈值电压Vth可表达为
(16)
(17)
(18)
再根据标准差计算公式及式(16),可得到短沟道SOI MOSFET器件由粒子数目波动引起的阈值电压标准差如下式所示。
(19)
3.2. 粒子位置波动引起的阈值电压波动
随着器件特征尺寸缩小,掺杂粒子位置的波动对阈值电压产生不可忽略的作用,粒子位置波动引起阈值电压波动
对总体阈值电压的波动影响比重可用系数Rp来进行近似描述,该系数可用电荷共享理论来解释,并采用数值模拟和实验提取相结合的方法来提取获得 [8] 。
(20)
(21)
文献 [8] 报道了Rp随
变化的关系曲线,本文参考该文献,利用函数拟合方法得到系数Rp。
(22)
式中,参数
和
可以通过仿真获得或由工艺代工单位提供相关工艺下的Rp计算获得。对于给定的工艺,也可以结合数值仿真拟合得到。
4. 结果与分析
RDF导致的阈值电压波动与器件沟道长度密切相关,本文通过比较Sentaurus TCAD的数值仿真结果与所建立解析模型的计算结果来进行模型验证。
图2给出了σVth与沟道长度的关系曲线。器件沟道长度为28 nm时,标准差为45 mV左右;当器件
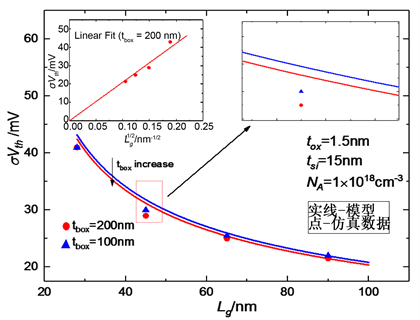
Figure 2. σVth versus channel length
图2. σVth与沟道长度的关系
沟道为90 nm时,阈值电压标准差急剧减小至20 mV左右。阈值电压标准差与
有着较强正比例关系。公式(22)能够反映出这之间的对应关系。但是由于Rp同样和沟道长度密切相关,随着沟道长度的下降,Rp逐渐增加,故在
较大时,实验数据点和拟合直线稍有偏离。
图3给出了σVth与NA的关系曲线。更高的掺杂浓度导致随机杂质波动造成阈值电压离散的扩大化。同时图中可知,器件的沟道长度较小时,阈值电压的波动越大,与模型预测结果吻合。阈值电压波动模型的预测值与实验仿真的结果一致,且
。因此,模型将为控制阈值电压的波动提供了理论依据,即可通过降低沟道掺杂浓度来抑制阈值电压波动影响。
图4为σVth与tsi的关系曲线。硅膜的厚度和均匀性直接影响FD-SOI MOSFET的电学特性。对于超深亚微米SOI MOSFETs而言,更薄的硅膜能够有利于器件及电路优良特性的展现,且较薄的tsi和低通道掺杂浓度器件对RDF具有较强的抑制作用。
图5给出了σVth与tox的关系曲线。当栅氧化层的厚度从1.0 nm增加到2.0 nm时,器件的σVth的变
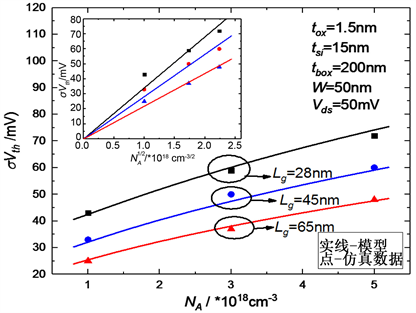
Figure 3. σVth versus channel length
图3. σVth与沟道长度的关系
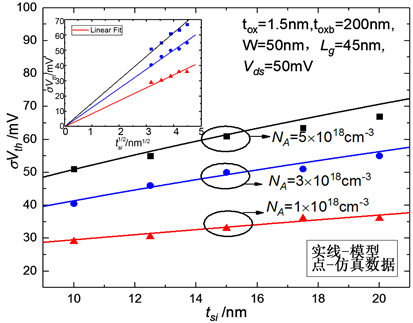
Figure 4. σVth versus silicon film thickness
图4. σVth与tsi的关系
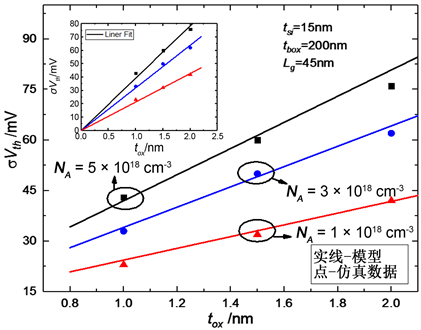
Figure 5. σVth versus gate oxide thickness
图5. σVth与tox的关系
化较大,可见其对阈值电压波动的影响较大。在不同浓度时,模型曲线σVth随tox变化的斜率不同。图中的线性拟合曲线说明,σVth与tox成正比,这与所获得的模型很好地匹配,即系数A2在近似情况下与tox成正比。
5. 结论
本文通过考虑掺杂数目和掺杂位置波动所引起的阈值电压波动,建立起来反应随机掺杂引起的超深亚微米SOI MOSFETs器件阈值电压模型,采用Sentaurus TCAD的数值仿真结果验证了所建立解析模型。依据模型计算和商用软件的对比计算结果,分析了随机掺杂情况下阈值电压随不同器件参数的波动变化情况,模型将为控制阈值电压的波动提供重要的理论预测。
基金项目
陕西省教育厅科研计划(16JK1609)。