1. 引言
传统的射线成像是利用物质对射线的衰减特性来对物体进行成像,常用于检测金属等重元素材料所构成的物质。但是,对于在医学和材料科学中,像人体的关节软骨,乳腺以及聚乙烯材料等这些以轻元素(例如炭、氢、氧和氮)为主构成的物质,它们对射线来说通常是弱吸收物质。对于这些物质来说,传统的射线成像方法几乎无法看到它们的内部结构,为弥补传统的射线成像方法在弱吸收物质成像方面的不足,射线相衬成像技术应运而生。与传统的利用物质对射线衰减性质进行成像的方法不同,射线相衬成像技术利用射线具“波粒二象性”的特点,通过探测物质引起射线的相移(即相位变化)来进行成像。
2. X射线光栅暗场成像理论概述
2.1. X射线基本原理理
如图1所示,X射线的产生我们通常采用X射线管装置。X射线的产生主要通过在真空管内由高电压作用下加速电子轰击阳极靶材,在电子轰击靶材时电子会骤然减速,这期间损失的动能会以光子的形式释放出来,所以X射线(X-ray)也称为连续辐射。通常X射线管的阳极靶材会选用钨靶、铜靶、钼靶等金属靶材 [1]。在X射线管中高压作用下加速电子会携带足够的能量去轰击靶材金属内原子的内层电子,则在金属原子的内层会形成电子空穴,同时外层电子会回到内侧电子空缺,由此就会使得高能级跃迁到低能级,而跃迁所产生的能量就是X射线(X-ray)。
X射线(X-ray)是电磁波,也具有“波粒二象性”。通常X射线(X-ray)以粒子的形式进行传播。在光子的特性下对于X射线的粒子进行解释为:
(1)
通过公式(1)中:
Ex为X射线光子的能量,单位为keV,
;
h为普朗克常数,其值为
;
v为振动频率;
c为光速,其值为
;
λ为波长,以nm表示。
通过上式的参数带入公式(1)可以的到
(2)
2.1.1. X射线(X-Ray)的几个特点
1) X射线同样符合光学射线的一般特性,在真空中沿直线传播,传播速度为光速,在磁场中不发生偏转。X射线的准直以及聚焦依赖的是X射线的反射性质以及直线传播性质。
2) 在X射线照射到物质时会发生衰减,呈倍数衰减,一部分X射线被物质所吸收,一部分X线穿过物质继续前进。
3) X射线能够与物质之间产生散射,散射可以分为想干散射和非想干散射两种。对于暗场成像来说,就是提取物质对散射能力的影响信息。
4) X射线可以同物质内层电子直接作用产生内层电子的激发,从而形成空穴,外层电子向内层跃迁从而放出X射线,即为特征X射线。
5) X射线能够与物质产生电离作用,能够让原本不带电的原子称为正负电分类的离子对,这种现象被广泛应用在对X射线的探测装置上。
2.1.2. X射线与物质的相互作用
X射线与物质的相互作用主要发生:光电效应、相干散射、非相干顿散射和电子对效应,因为电子对效应只能在光子能量大于1.02 MeV的时候才能发生,在低能下的X射线的衰减主要是由物质对X射线的光电吸收和散射引起的。下面简单介绍一下这几种效应。
1) 光电效应:在光电效应过程中,辐射光子从原子逃逸出原子层电子并成为自由电子。光子的能量克服了电子结合能量以电离原子,其余能量是光电子的动能。这种现象被称为光电效应。
2) 相干散射(称为瑞利散射):低能的X射线与束缚电子相互作用跃迁后能量并没有发生转移,而只是将散射光子的方向发生改变。其波长、频率都没有发生任何的改变。相干散射的发生概率与物质的原子序数和X射线能量大小有关,当入射X射线光子能量小于50 keV时,X射线的散射主要是相干散射,当X射线能量不断增大时相干散射开始变小。
3) 康普顿散射入射的X射线光子与物体原子的外层电子撞击后,其中一部分能量使电子射出形成反冲电子,同时降低能量的入射X射线光子传播方向发生改变。
4) 电子对效应:当入射光子的能量大于两个电子的静止能量使,入射光子会与介质原子核周围电场发生某种作用,使入射光子的能量转化为一个正电子和一个负电子形成的电子对,这种现象称为电子对效应。
X射线与物质的相互作用的机制主要有:光电效应;康普顿效应;瑞利散射和电子对效应,其中康普顿效应和光电效应发生的几率比较大。
2.2. X射线光栅暗场成像基本原理
2.2.1. Talbot自成像
X射线光栅暗场成像基本原理就是通过Talbot效应,在相干光条件下在一定距离上获得光栅的自成像 [2]。
Tablot自成像就是(如图2)光栅在相干光照射下在Tablot的距离处可以得到光栅的自成像。光栅在Tablot距离处加入另一个光栅时,在相干光照射下就会在第二块光栅后获得摩尔条纹 [2]。
根据Talbot自成像可知,G1相位光栅在不同的特定距离可以获得光栅的自成像,可用公式表达:
(3)
由公式(3)中dN为Talbot距离,N是Talbot级次,p1为相位光栅G1的周期,λ是波长。
2.2.2. Talbot-Lau干涉的光栅成像技术
Pfeiffer在2006年提出了在常规X射线光源上使用Lau效应 [2] [3] [4] 并且提出了基于Tablot-Lua干涉法的光栅成像方法。整个装置示意图如图3所示。
如图3利用在常规X射线源的条件下建立基于Talbot干涉光栅成像系统,因此引入了源光栅G0在光栅成像系统中,这就是Talbot-Lau干涉仪。
整个基于Talbot-Lua干涉法的光栅成像系统主要由光源和三块光栅组成。这三个光栅分别为:G0 (源光栅)、G1 (相位光栅)、G2 (吸收光栅)。其中G0源光栅的作用就是把光源分成许多个线光源,并且各个线光源之间互不相干,但是每个光源又是相干光源。
3. 构建X射线光栅暗场成像系统
3.1. 暗场成像系统设计
Kafri在可见光领域提出了利用非相干光照明的方法来测量气体的光学性质 [5] [6]。也就是在任何光
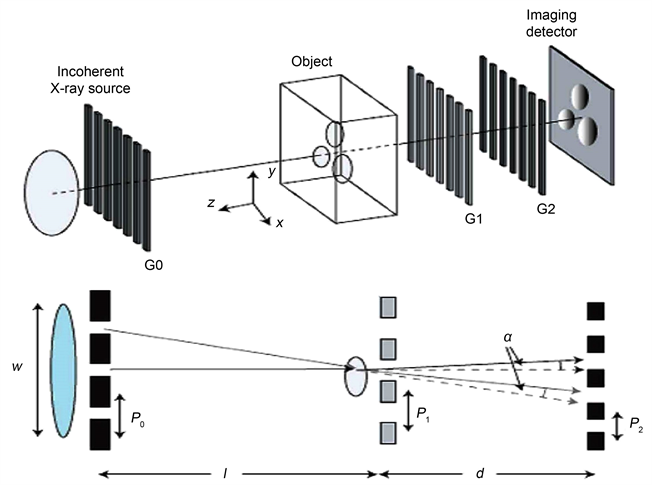
Figure 3. Grating imaging method sketch of Talbot-Lua interferometry
图3. Talbot-Lua干涉法的光栅成像方法示意图
源条件下,通过光源照射时多个周期能够产生莫尔条纹的的特性 [7] [8]。
在系统中加入源光栅G0能够实现在Talbot效应对X射线部分相干光的限制。通过源光栅G0在相位光栅处可直接获得非相干光的投影,并且投影与吸收光栅G2能够产生莫尔条纹。光栅满足几何条件:
(4)
L0是源光栅G0到相位光栅G1的距离,D为相位光栅G1与吸收光栅G2的距离,系统总长为
。
对于X射线源焦点大小来说,在加入源光栅G0后,光源被分为许多个互不相干的小光源,他们对相位光栅G1满足:
(5)
小光源投影满足:
(6)
同时周期错开摩尔条纹相互叠加也可得出三块光栅G0、G1、G2周期的关系:
(7)
在光栅暗场成像中,光栅的选择尤为的重要。通常要选择能使光源的衍射程度好并且可以消除0级衍射信息的。因此G1相位光栅的表达式是 [9]:
(8)
在公式(8)中T是光栅厚度,
为光栅的相位因子。
在光栅材料的选择上,首先由于光栅厚度一定,材料可以选取的有:C、Li、Al、Si、Ni、Cu、Ag和聚甲基丙烯酸甲酯等材料。
光栅成像几何条件的约束,通常对于系统总长的会根据系统搭建的选取来确定(在这里将系统长度作为已知来确定其他系统参数指标)。对于系统中的光栅选取,首先三个光栅中相位光栅G1周期最小,并且在实际中工艺极限对光栅尺寸也有一定的限制。因此对于相位光栅G1来说设置为极限值为已知量。则可推出得到其他参数条件。
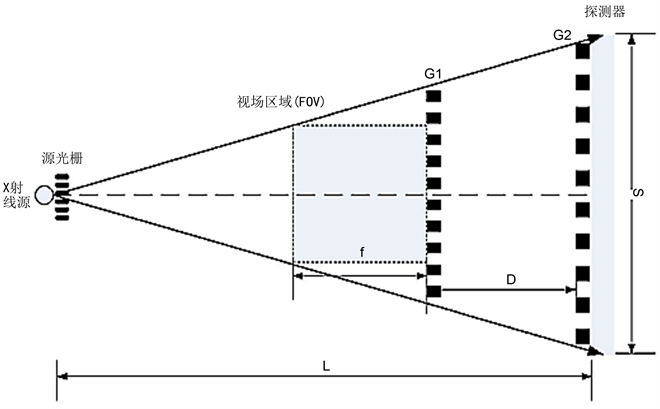
Figure 4. Grating imaging system schematic diagram
图4. 光栅成像系统示意图
如图4可知L为系统总长,f为视场大小,S为探测器尺寸。因此可以推导出:
1) 通过S和f确定的关系是:
。
2) G2吸收光栅的周期p2:
。
3) 源光栅G0的周期p0:
。
3.2. 蒙特卡罗方法构建X射线源
3.2.1. 蒙特卡罗方法
蒙特卡罗方法(Monte Carlo, MC)是一种数学统计法,又称为随机抽样法 [10] [11] [12]。通过建立数学模型,利用数学统计的方式将数学计算转化为随机抽样,并且通过统计方法得到一个最大几率的数值。随着时代的发展,计算机的普及和应用,蒙特卡罗方法(MC)得到了完善的利用,通过对事件的发生概率或随机期望值的抽样统计,通过随机抽样的概率和平均值来体现和描述为某个事件的结果或者其发生的概率。蒙特卡罗方法(MC)的应用范围非常广泛,在物理学(粒子输运过程、粒子与物质之间的作用)、天文学、经济学等方面都有着重要的应用价值 [13] [14] [15]。
蒙特卡罗方法(MC)在物理学领域有着很重要的应用,已经发展成为一个学科来辅助物理学方面的研究,特别是对于粒子计算上尤为突出。蒙特卡罗(MC) Monte Carlo方法是一种随机过程方法,他并不严格去求解一些物理方程,而是通过模拟拟单粒子在介质中的随机运动过程,然后将大量粒子的平均结果作为系统结果的近似,给出粒子系统在介质中运输的最后结果 [16]。X射线与物质的相互作用就属于是一种随机抽样事件,因此对于X射线成像研究利用蒙特卡罗方法(MC)是完全可行的 [17] [18]。
3.2.2. 基于蒙特卡罗方法的MCNP5介绍
基于光栅成像暗场成像模型建立,通过MCNP5来实现。MCNP5程序全称Monte Carlo N-Particle Transport Code System,它是利用Monte Carlo方法模拟解决多粒子运输系统中粒子输运问题。Monte Carlo方法它是一种随机过程方法,不是精确地模拟一些物理方程,而是模拟准单粒子在介质中随机运动的过程,然后将许多粒子的结果平均到系统中作为近似的结果。运输媒介的最终结果。MCNP程序可用于处理中子,电子和光子的传输过程。其中中子能量范围为10−11 Mev~20 MeV,光子、电子能量范围为1 KeV~1000 MeV [17] [18]。
选用MNCP5仿真主要其功能全面能够计算各类高能粒子与物质的相互作用,由于构建模型只需要对对应源卡进行书写相对简单,兼容PC端较好。虽然MCNP5为半开源软件但自带数据包能够计算绝大多数的粒子输运的过程。
如图5 MCNP5模拟仿真软件的程序流程图。
基于MCNP5仿真的流程如图,在MCNP5中所有的模型建立都要遵循整个流程的要求,书写代码时要按照格式要求和构建模型的几何说明 [19] [20]。
· 标题卡标注文件的名字和相关的注释对仿真计算没有相关联系。栅源卡的书写是MCNP5的主要组成部分;它主要是对几何的空间关系进行定义。对于仿真模型的空间进行区域划分。MCNP5中要求所有的模型都要在栅源卡中有明确的空间几何定义,对空间的定义MCNP5采用的是三维(x, y, z)笛卡尔坐标系。所有维度都以cm为单位。对于栅源卡中区域的划分是用区域的交、并、补运算定义的。每个单独的空间关系都要有一个cell来单独定义。栅源卡除了对空间位置的定义在对应单独的cell中可以定义与粒子是否发生关系、该物质的密度和空间内移动等。
· MCNP的曲面卡就是对栅源卡对应cell进行空间几何定义,确定真实的大小位置关系等对应具体补充。
· 源定义是对射线源的定义说明,MCNP中可以随意定义源的形状大小空间位置等因素。通过向量关系确立源的方向性。
· 粒子数和仿真时间的设定是在MCNP中为了计算物质与粒子作用关系可以确定粒子数与物质进行计算也可以确定时间来获得相对应的粒子数。MCNP中有多种探测器的选择对于不同用途进行了区分 [21] [22]。
4. X射线光栅成像暗场成像图像降噪研究
4.1. 暗场成像信息提取算法
4.1.1. 相位步进数据采集过程
X射线光栅暗场成像系统主要作用就是能够提取X射线暗场图像信息,通常我们使用相位步进法提

Figure 5. Grating imaging system schematic diagram
图5. 光栅成像系统示意图
取图像信息。相位步进法采集过程是基于Talbot-Lau干涉法的成像系统。
相位步进法的成像过程就是移动系统中其中一块光栅,每次移动的距离是等距离,并且总移动长度为移动的光栅一个周期。每次移动光栅的同时让探测器记录下该时刻的光强信息。并通过计算提取所需的信息。
由于暗场成像的提取信息就是通过物质的散射性质在系统中产生的莫尔条纹变化的部分,所以需要在测量时获得背景信息。也就是在该成像系统中,提取信息需要记录两组信息。在等等距离下先记录背景位移曲线,然后放入被测物体记录有被测物体时的光强图像。最后通过图像对比位移曲线获得散射信息。如图6,图7所示。
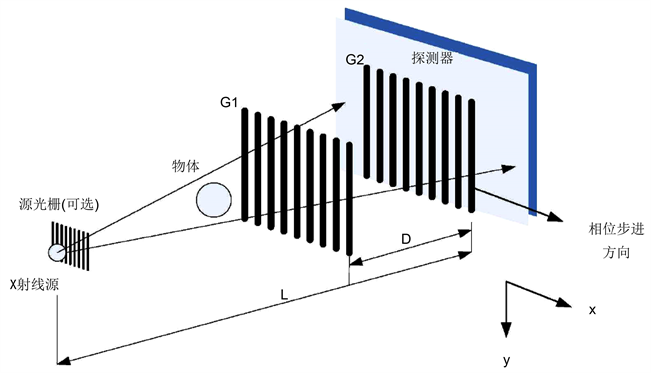
Figure 6. Structural sketch of raster-based dark-field imaging system
图6. 基于光栅暗场成像系统结构示意图

Figure 7. Schematic diagram of phase stepping method
图7. 相位步进法原理示意图
4.1.2. 暗场信息提取
基于Talbot-Lua干涉X射线光栅暗场成像信息的提取原理在没有被测物体时,G1相位光栅在G2吸收光栅上可以获得均匀的摩尔条纹。当相位光栅做水平步进位移时,在探测器上每个像素点能够得到一条位移曲线。当有被测物体放入光栅成像系统中时,探测器上的位移曲线会因为被测物体的对X射线造成的散射改变位移曲线的对比度,而对比度的差别就是暗场信息(散射信息)。
X射线与物质的散射作用为小角度散射,其散射分布为
,
为原散射角,则可得:
(9)
在高斯分布中散射角可以表示为
(10)
可以表示物质的散射程度,能够体现物质的散射能力和物质的组成信息。
当直射光穿过物体时其散射角度可以表示为
(11)
设置光强为
,k为第k步的位置。N为步数则:
(12)
在扣除背景通过得到的光强信息可以得到散射信息为:
(13)
散射信息就是背景曲线与被测物体曲线的对比度。则曲线的对比度通过傅里叶系数获得:
(14)
(15)
二者比值为:
(16)
同时考虑通过傅里叶变换可得:
(17)
将(16)和(17)合并可得:
(18)
4.2. 基于蒙特卡罗仿真建立成像系统模型
4.2.1. 建立光栅暗场成像模型
X射线光栅暗场成像检测系统基于蒙特卡罗方法(MC)MCNP5建立仿真模型。首先由第二章总结可知确定系统的定量参数。因为已知首先确定光栅成像的系统总长度。然后确定相位光栅G1,G1光栅周期我们可以先设置为理想值为p1 = 2 μm。则通过公式(4)得到源光栅G0和吸收光栅G2的值。即p0 = 4 μm,p2 = 4 μm。光栅材料上选取金为光栅。源能量大小设置为30 KeV。粒子数为500,000,000个。选取探测器为成像面板像素选取为500 × 500与吸收光栅G2近贴。相位光栅G1可沿水平方向位移,位移步数为5。
4.2.2. 模拟实验
同过上述的参数设置仿真获得的图像如图8。

Figure 8. Moire fringes obtained by simulation
图8. 仿真获得的莫尔条纹
通过观察图8摩尔条纹清晰均匀符合预期的效果。
在得到摩尔条纹后可证实光栅暗场成像系统模型参数合理,仿真图像能够看出光栅的周期不同因此在平行放置时能够出现清晰的摩尔条纹。这与实际的文献中提到的效果相符合。
进一步我们通过相位步进法提取暗场信息。按照理论要求首先获取背景信息,在周期为2 μm的G1相位光栅中进行步进位移,一次移动0.4 μm可获得五幅背景图像信息。同时由于仿真过程中步进位移能精准的位移每一步,而在实际的图像提取中光栅位移所带来的机械误噪声差对成像质量来说也十分重要,因此做步进位移提取图像时我们在移动距离上加入了误差值。如图9。
我们在仿真系统中加入一个小立方体密度选取材料为乙烯。乙烯的密度与人体软组织近似,X射线对乙烯等轻质元素的吸收效果较差,因此我们尝试同过散射图像获取其形状信息,同时也可以证明暗场成像对。
用步进位移在有被测物体的情况下仿真获取图像如图10。
通过4.1.2中的提取公式我们提取光栅暗场信息的原始图像可得如图11。
4.3. X射线暗场图像数字化处理
在上一节中我们通过光栅暗场成像信息提取方法提取处暗场图像信息。从图11中也能看出在提取图像的同时我们也根据实际情况在系统仿真模拟时加入了误差因此我们获取的图像也存在噪声。
4.3.1. 暗场成像噪声分析
X射线光栅暗场成像检测中,获取图像会受到X射线管光强分布不均匀造成莫尔条纹对比度的下降,

Figure 9. Five background pictures obtained by phase stepping
图9. 相位步进获得5幅背景图片

Figure 10. Five images with the object under test
图10. 在有被测物体下的五幅图像

Figure 11. Dark field information original image
图11. 暗场信息原始图像
造成图像提取质量的下降。步进位移采集图像过程中的机械误差,会对获取图像信息的准确性造成影响。以及粒子的随机噪声等都会对获取图像质量造成影响 [23]。
噪声的存在会大大降低对于检测物体图像质量,也不便于观察到图像当中的特征信息因,从而造成对检测结果的判断失误,因此对于提取的原始图像进行降噪处理也是非常必要的 [24]。
4.3.2. 平滑滤波
平滑滤波器是一种低频增强的空间滤波技术,通过窗口式的滤波窗口对图像进行处理。滤波窗口通过图像相邻内的像素平均值来代替图像中的像素值。平滑滤波是均值降噪方法,它能够去除图像中大量的噪声,但同时平滑也会造成图像质量的模糊,造成信息的缺失。
通常在图像大小为
的图像,通过
大小的滤波窗口对图像进行滤波。则点
的像素:
(19)
在通过Sobel滤波之后再对图像做平滑处理在,确保图像边缘信息的情况下做平滑处理,能够降低误差带来的图像噪声如图12。
通过对图像进行平滑处理从而降低了机械误差带来的噪声影响。
4.3.3. Sobel滤波
Sobel算子是一种经典的边缘检测的线性高通滤波器,算子中有两组
的矩阵,分别为横向和纵向,在与图像做水平卷积,能够得到横纵的亮度差的近似值。
(20)
(21)
通过对每个像素的纵向和横向的梯度近似值得:
(22)
计算梯度方向:
(23)
在衰减图像中对图像锐化以及边缘描述可通过高通滤波来实现,高通滤波会变换衰减傅里叶变换中的低频部分但是不会扰乱高频信息。因此利用Sobel滤波后如图13所示。
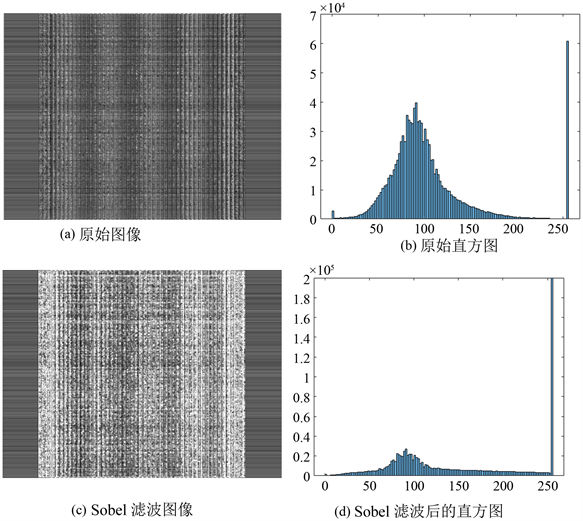
Figure 13. Sobel filter image and histogram intention of X-ray dark field image
图13. X射线暗场图像Sobel滤波图像及直方图示意图
如图13中通过Sobel滤波处图像中的物体形状更加清晰,体现的更加清楚。在对原始图像进行滤波处理后,我们获得了图像较为清晰的边缘信息。
4.4. 图像处理结果分析
通过对暗场图像的提取我们获得了暗场原始图像,但是图像同样伴随着噪声,因此我们利用Sobel滤波技术能够对图像的边缘细节进行增强,在将图像做一定的平滑处理降低图像中的噪声,但是平滑滤波对图像细节的信息丢失太多。从通过Sobel滤波而我们能够清楚的看出图中的正方形乙烯块。对于乙烯这类轻质元素,物质X射线吸收效果较差,而暗场成像通过X射线对物质的散射作用在基于光栅暗场成像系统中将散射信息进行提取,从而获得我们能够直观观察到的暗场图像。
5. 结论
本文主要对基于普通光源光栅暗场成像系统中成像系统结构分析和优化,研究X射线源对暗场成像系统的影响和光栅暗场成像暗场信息提取算法,并对暗场图像降噪方法进行深入的研究。通过对光栅暗场成像系统噪声的分析对图像进行数字化图像处理,射线光栅成像能够在一次数据采集过程中提取物质衰减、相衬和暗场三种,从而形成“三位一体”的成像方式。其可以工作在常规光源下,因此具有非常好的临床应用前景。论文从系统,信息提取与图像重建三个层,递进的方面出发,对现有的射线光栅成像技术中的物理问题和算法问题进行研究,最终完善了射线光栅成像从系统到最后的图像重建这一框架。
1) 对X射线成像原理进行介绍,进一步对基于X射线光栅暗场成像检测方法的原理做了细致认真的总结。同时也对X射线光栅暗场成像系统参数和结构优化做出论证。
2) 通过蒙特卡罗(MC)方法的MCNP5仿真软件设计X射线源,对X射线源进行仿真分析。
3) X射线光栅暗场成像图像提取方法的研究,采用相位步进法提取X射线光栅暗场成像信息,对所提取的暗场图像信息进行降噪处理。采用Sobel滤波的处理方式提高被测物体的图像质量。
参考文献
NOTES
*通讯作者。