1. 引言
无线激光通信技术是指利用激光束作为载波在自由空间直接进行语言、数据、图像等信息传输技术。自由空间包括大气信道和真空信道。在真空信道中,几乎不存在大气对通信链路的影响,而大气信道存在了大气散射、大气吸收、大气湍流等现象,对激光波段影响较大,特别是大气湍流,大气湍流造成了接收信号时强时弱,是无线激光通信中误码产生的主要因素,因此从无线激光通信技术发展的初期,人们就针对无线激光通信的通信链路设计中增加纠错码进行了研究。
2. 大气湍流对激光通信的影响 [1]
由于大气湍流影响,到达接收端的光束波前幅度及相位发生畸变,使光斑中心产生光漂移和扩散现象。对于较强湍流条件,甚至产生光斑破碎和光斑空洞现象。大气湍流散斑效应引起光斑空间分布变化,并将影响接收端接收探测器的效率。在弱湍流条件下,链路距离L、接收口径D、大气折射率结构常数
对应关系满足以下公式:
在无线激光通信系统,系统衍射极限角
所对应的最大分辨力为
。由于受到大气层段到达角起伏湍流效应的影响,激光通信系统的最大分辨力将会降低为:
由此可见,大气湍流散斑引起的分辨力下降将引起接收端信号光接收的功率,接收功率会影响到整个通信系统的误码率。
在无线激光通信中一般采用纠错码技术来降低无线激光通信产生的误码。
3. 纠错码技术 [2] - [9]
纠错码技术是通过在发送端传输的信息序列中加入一些冗余的监督码进行纠错。在发送端由发送设备按一定算法生成冗余码插入到要传输的数据流中,接收端按同样算法对接收到的数据流进行译码,根据接收到的码流确定误码的位置并进行纠错。最众多编码方法中,应用较广泛的有RS码、Tubro码和LDPC码等。
3.1. RS码
RS码首先由Reed和Solomon于1960年构造出来,是目前最为有效、应用最为广泛的差错控制编码之一,是一类具有很强纠错能力的多进制BCH码,它不仅可以纠正突发错误,还可以纠正随机错误。
具有纠正t个错误的RS码由如下参数:每个符号比特数m;每个符号可以看成是有限域中的一个元素;码长
;信息段有k个符号;监督段有
个符号;最小码距离
。RS码用于纠正的突发错误图样是:总长度为
比特的是i个突发。
RS码的一个重要性质是:真正的最小距离总是相同的。每种RS码都是一个最大距离的可分码,最小距离等于n − k − 1。当省掉RS码的某些信息符号后,分组长度缩短,但是最小距离并不减小,故任何一种缩短的码仍是一个最大距离可分码。
RS码的另一个重要形式是在其码字内的任何k个位置都是可用信息集合。(n, k)RS码中,输入信息分成km比特一组,每组包括k个符号,每个符号由m比特组成。RS码的编译码是基于一组码元而不是单独的0或1,这也是RS码纠错能力特别强的原因,这也使得RS特别适合处理突发错误。
3.1.1. RS编码原理
RS(n, k)码具有以下性质:
n为码长,k为信息位长,n − k为校验位长。一般
,
,q为有限域的阶数,是素数或素数的幂次,实用中一般取q为2的幂次。最小距离为
,t为设计的纠错能力。RS码主要是围绕生成多项式构成的,其生成多项式为:
a为GF(q)域上本原多项式的根,a的各次幂可构成扩域GF(qm)上的所有元素。
编码器结构示意图如图1。
3.1.2. RS码译码原理
RS译码分为以下几步:
第一步:计算多个伴随式值;
第二步:由伴随式值确定差错定位多项式;
第三步:求出错误位置值;
第四步:由所得的错误位置值计算错误值;
1) 伴随式的求解
设G(q)是RS码所在的伽罗华域(Galoisfield),n为RS码的编码长度,q是一个不为1的素数或者素数的幂,t为RS码的纠错长度,则RS码的生成多项式为:
由编译码理论可知,对于以上式为生成多项式的RS码,其校验矩阵为:
设接收到的码组为R(x),其系数矩阵为:
,且设信道产生的错误码数
2) 差错位置多项式的确定
鉴于非线性方程直接求解比较困难,因此引入一个称为错误位置多项式的中间变量σ(x),先求出错误位置数xi,再求出
,给出如下定义:
设
,
,L,
是σ(x)的解,由σ(x)的定义有
所以求错误位置就是求解错误位置多项式。
3) 关键方程的求解
关键方程的求解可通过ME迭代算法来实现。
ME迭代算法可以简单描述为以下几个公式和约束条件的迭代。首先初始化:
;
;
;
;迭代后如果
或
小于8,则算法迭代结束。此时
,
。
4) 错误位置的确定
求得σ(x)后接下来就要求出它的根,这个过程可以用钱搜索来实现。设
为了要检验第一位
是否错误,相当于译码器要确定
是否是错误位置数,这等于要校验
是否是σ(x)的根。若是,则有:
所以得到了σ(x)后,为了译
,译码器首先验证
是否成立,若成立则α是错误位置数,
码元是错误码元;否则
是正确的。
同理为了译
,译码器必须验证
是否成立,若是则
是错误码元,若不成立,则
不是错误码元。
这样一次对每一个
进行检验,就求得了σ(x)的根,这个过程称为钱搜索。
5) 差错幅值的求解
差错幅值的求解通过Forney算法来实现。Forney算法描述如下:
若实际产生错误个数
;则
,同时得到
所以错误值为
。
3.2. Turbo码
Turbo码是C. Berrou等人提出了一种新型的纠错码。它采用一种并行级联的方法实现了长码的编码,同时构造了相应的解码器来完成长码的解码,是一种实用的纠错码,它的性能非常逼近香农的性能界,使其在较低的信噪比条件下仍能够保持良好的性能。目前Turbo码在CDMA的应用得到各国学者的重视,Turbo迭代的思想已经渗透到物理链路层先进的信号处理技术的各个领域,它域调制、均衡、空时编码和OFDM相结合极大的促进了技术的进步和发展。
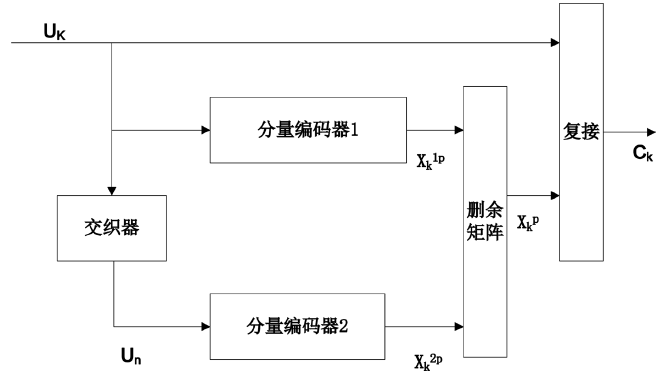
Figure 2. The sketch map of turbo encoding
图2. Turbo码编码框图
图2表示了经典的Turbo码编码框图,它主要由分量编码器1、分量编码器2、交织器以及删余矩阵和复接器构成。分量编码器一般选择为递归系统卷积码(RSC),通常两个分量编码器采用相同的生成矩阵。因此Turbo码又被称为并行级联卷积码。
在Turbo码编码过程中,两个分量编码器的输入序列是相同的,长度为N的信息序列
在送入第一个分量编码器进行编码的同时作为系统输出
直接送自复接器,同时
经过交织器I后的交织序列
送入第二个分量编码器。其中,
,
。
为交织映射函数,N为交织深度,即为信息序列长度。两个分量编码器输入序列仅仅是码元的输入顺序不同。两个分量编码器输出的校验序列分别为
和
。为了提高码率和系统频谱效率,可以将两个校验序列经过删余矩阵删余后,再与系统输出
一起经过构成码字序列
。
交织器和分量码的结合可以确保Turbo码编码输出码字具有较高的汉明重量。在Turbo编码器中交织器的作用是将信息序列中的比特顺序重置。当信息序列经过第一个分量编码器后输出的码字汉明重量较低时,交织器可以使交织后的信息序列经过第二个分量编码器编码后以很大的概率输出高重码字,从而提高码字的汉明重量;同时好的交织器还可以有效的降低效验序列间的相关性。通过交织,编码序列在长为2N或3N比特的范围内无记忆性,从而由简单短码构造近似随机长码。交织器实际上是一个一一映射函数,作用使将输入信息序列重的比特位置进行重置,以减小分量编码器输出效验序列的相关性和提高码重。因此,交织器设计的好坏在很大程度上影响Turbo码的性能。删余矩阵的作用是提高编码效率,其元素取自集合{0, 1}。矩阵重每一行分别余两个分量编码器对应,其中“0”表示相应位置上的效应比特被删除,而“1”则表示保留相应位置的效应比特。
3.3. LDPC(低密度奇偶校验)码
LDPC码是Gallager于1962年提出的一种性能接近于香农限的好码,限于当时计算机水平和硬件技术LDPC码在很长一段时间内一直未受到人们重视,直到Berrou等人提出Turbo码后,LDPC码才重新引起人们的研究兴趣并成为研究的热点。计算机仿真结果表明,最好的非规则LDPC码(长度为106)可获得在BER = 10−6时仅偏离容量0.13 dB的性能,优于迄今所知道的最佳Turbo码,当码长为107码率为1/2时,其性能距香农限只差0.04 dB。
LDPC码的特点是:性能优于Turbo码,具有较大灵活性和较低的差错平底特性;译码复杂度低于Turbo码,且可实现完全的并行操作,在编码器和译码器之间不需要交织器,硬件复杂度低,因而适合硬件实现;吞吐量大,适合高码率的应用,极具高速译码潜力。此外,LDPC码在干扰、衰落等原因引起的突发误码情况下有更优良的性能。但LDPC码在硬件实现上难点是它的不规则结构,大部分的LDPC码的结构都是非常随机的,使得它的编码器要比Turbo码的复杂一些。另一个缺点是不能灵活地改变码率和码长,要改变通常需要重新构造奇偶校验矩阵和相应地生成矩阵,使得硬件改动困难。
图3给出了4种不同的帧长,即N = 2048 bits、N = 1024 bits、N = 512 bits、N = 256 bits,它们的码率R都为1/2,(3, 6)规则的LDPC码。图3可以很明显地看出:在相同码率的情况下,随着码长的增加性能会越来越好,这是码字间的码距随着码长的增加而增大的结果。
高速LDPC编译码器硬件实现的关键在于码结构以及译码算法的选取。为适合高速硬件实现,一般应选用准循环结构的LDPC码。准循环结构使得编码器可以用移位寄存器快速实现,而译码器高速实现的关键是并行度的选取以及译码算法的选取。
4. RS码在无线激光通信链路中的应用
通过对上述几种纠错码的分析,设计了一套无线激光通信设备,在链路中采用RS (255.239)码型,通信速率为256 kbps,通信距离3 km,进行了实际的试验,分别采用未加纠错码和增加纠错码两种体制,记录了实际的误码率。在实际的试验过程中,可以采用增加人为的误码,使系统产生需要的误码。结果如下:
从图4可以看出,RS码在小于10−4时,基本上可以完全进行纠错,而使系统的误码率基本上为0,上述试验排除了通信链路中光遮挡的情况。
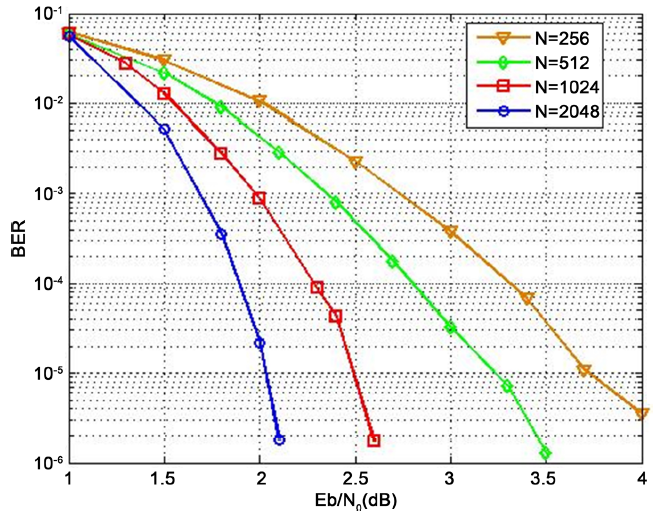
Figure 3. The compare of difference frame
图3. 不同帧长的性能比较

Figure 4. The error-code-rate between encoding and nun encoding
图4. 未加RS码与增加RS码误码率对比图
5. 结论
本文分析了大气湍流对激光通信的影响,并分析了几种常用的纠错码码型,重点分析了RS码的编码与解码过程,并在此基础上设计了一套无线激光通信端机,采用RS (255.239)码型,在误码率小于10−4时基本上可以把误码全部纠错,使误码率达到0。通过对实际的试验表明了RS码可以有效降低通信误码率。
参考文献