1. 引言
气候变化造成了包括自然灾害和极端气候事件在内的一系列问题,已受到了科学界与社会大众的普遍关注。全球气候变化对水文过程有重大影响 [1] ,亟需研究气候变化条件下水文水资源的变化规律和趋势。为了更精确估算大区域和全球水资源量,预测气候变化的水文响应,大尺度乃至全球尺度水文模型已成为全球气候变化影响研究的重要技术手段 [2] 。
大尺度水文模型研究起步较晚,但也取得较大进展。Döll [3] 等人于2003年提出了WGHM模型(Water GAP Global Hydrology Model);Liang [4] 等人在VIC-2L (Variable Infiltration Capacity)模型基础上改进开发了VIC-3L模型;Vörösmarty [5] 等人构建了WBM (Water Balance Model)模型;Arnell [6] 等人构建了Macro_PDM (Macro-Probability Distributed Model)模型。
WASMOD (Water and Snow Balance Modeling System)的当前版本由Xu [7] 等人基于NOPEX的流域开发。Widén-Nilsson [8] 等人在原本的WASMOD基础上构建了大尺度水量平衡模型WASMOD-M,Gong [9] 等在WASMOD-M月尺度模型的基础上建立了半分布日尺度WASMOD模型。目前WASMOD模型已有月尺度、日尺度模型,能满足流域尺度、区域尺度甚至全球尺度的水文模拟。
月尺度WASMOD模型应用广泛,已在全球范围内多个流域得到验证。Xu [10] 等用WASMOD模型来研究中国六个流域的月径流,并获得了较好的模拟效果;Widén-Nilsson [11] 等人在原WASMOD基础上构建了大尺度水量平衡模型WASMOD-M,并在世界范围内得到应用检验,结果表明尽管WASMOD-M仅针对长期平均径流进行校准,但长期平均年内径流变化与之前公布的大多数径流站的结果一致;Eregno [12] 等采用HBV和WASMOD这两个水文模型来研究三个流域对气候变化的水文响应,并比较两种水文模型之间的差异,最后发现两个水文模型在重现以往的径流时效果都较好;在不同的气候改变模式下,二者的模拟结果有较大的差异。Kizza [13] 等将有资料地区率定得到的参数,移植到其他子流域来模拟维多利亚湖的入湖流量,结果证明参数移植获得了良好的模拟效果。李占玲 [14] 对月尺度WASMOD在莺落峡流域运用时对模拟残差进行统计特征检验,最终发现当对原始数据进行开根号处理时,得到的模型残差可以通过相互独立假定、同方差假定和正态分布假定。Li [15] 等在非洲南部,比较TRMM和WFD两个数据集作为降雨数据输入时,半分布日尺度WASMOD的径流模拟效果差异,结果表明修正后的WFD比TRMM数据集的效果更好。
半分布式日尺度WASMOD模型的汇流算法为Network Response Routing (NRF)。Gong等 [9] 发现:相比于Linear Reservoir Routing (LRR)汇流算法,NRF汇流算法拥有独特的优势。地形数据给定时,汇流模拟精度与模型的空间分辨率无关。
NRF汇流算法可以在所有尺度保留高分辨率地形数据的汇流滞时空间分布信息,在大尺度分布式水文模型的研究方面具有重要的价值。但该算法没有考虑流域的下垫面的影响,不能适应多种流域下垫面情况下的汇流计算。在不同的流域下垫面影响下,同样的坡度对流速的影响程度是不一样的,在本文的研究中发现部分流域计算得到汇流时间相较实际经验值偏长。
为了优化半分布式日尺度WASMOD模型汇流算法,解决不能适应所有地形条件的问题,本文将基于DEM的等流时线法 [16] 与原汇流方法NRF结合,可以更好地适应在不同尺度和不同流域下垫面的影响下,流速对坡度的影响程度的变化。对WASMOD汇流方法进行改进,使得改进后汇流计算在不同的流域中适应性更强,同时对改进后的模型在湘江、雅砻江和汉江流域进行应用分析,验证改进半分布式日尺度WASMOD模型的径流模拟效果,发现改进后,汇流时间计算结果较经验值更加合理。
2. 研究区和数据
2.1. 研究流域
本文选择的研究区为湘江、汉江以及雅砻江流域。在三个流域分别测试模型性能,用以验证汇流方法改进后模型的有效性和普适性。三个流域的气象类型和下垫面条件等均有所不同。因为三个流域的地形和下垫面条件不同,所以可以测试改进后的汇流模块是否能够在不同流域中准确计算汇流时间。
研究区气候与地形特性信息见表1,基于Hydro1k数据集,计算在集水面积阈值为6000 m2时各流域的河网密度。流域形状系数为流域分水线的实际长度和与流域同面积的圆的周长之比。
Table1. Climate and topographic characteristics information for study regional
表1. 研究区气候与地形特性信息
为分析各流域坡度分布,基于各流域1 × 1 km格网地形数据,采用D8流向法计算出各水文站控制流域所有格网的坡度,并绘制其坡度—频率直方图,如图1。
对于各水文站点控制流域,其降水较多月份的水量空间分布具有一定的特点。甘溪水文站控制流域的雨量空间分布主要特点为:4月、5月主要集中在流域东北部和北部,之后逐渐转移到东南部。雅江水文站控制流域的雨量空间分布主要特点为:降雨主要集中在下游区。白河水文站控制流域的雨量空间分布主要特点为:4月到7月降雨主要集中在流域南部,从8月开始转移到流域西部。
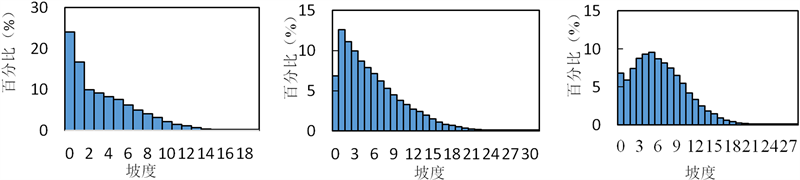 (a) 甘溪站控制流域 (b) 雅江站控制流域 (c) 白河站控制流域
(a) 甘溪站控制流域 (b) 雅江站控制流域 (c) 白河站控制流域
Figure 1. Slope-frequency histograms for study area
图1. 研究流域坡度~频率直方图
2.2. 研究数据
高程数据集为Hydro-1k数据集 [17] 。Hydro1k数据集是由美国地质勘测局地球资源观测系统数据中心与联合国环境计划—全球资源信息中心联合制作的一个全球数字地形高程模型。其分辨率为1 × 1 km。
WASMOD模型所需气象信息为降雨,温度,和相对湿度。降雨和温度数据分别为国家气象中心发布的中国地面降水日值0.5˚ × 0.5˚格点数据集和中国地面气温日值0.5˚ × 0.5˚格点数据集(http://data.cma.cn/site/showSubject/id/46.html)。站点日径流数据采用水文站实测数据。甘溪水文站采用1999~2009年日径流数据,雅江水文站采用1998~2008年日径流数据,白河水文站采用1980~1990年日径流数据。
3. WASMOD模型及汇流方法
3.1. WASMOD模型介绍
WASMOD是一个水量平衡模型,模型概念简单,参数较少,模型结构图如图2。模型包括降水下渗、蒸发、产流和汇流等四个模块 [18] ,每个过程模块的参数如表2所示 [15] 。
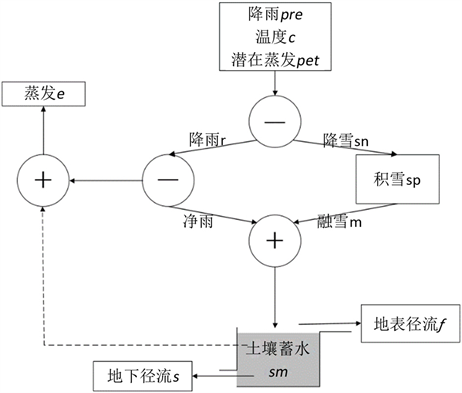
Figure 2. The concept of the WASMOD model system
图2. WASMOD模型概念图

Table 2. A list of parameters for WASMOD model system
表2. 产流参数汇总表
3.2. NRF汇流方法及问题
半分布式日尺度WASMOD模型的汇流模块为Gong等提出的Network Response Routing算法,简称NRF汇流方法 [9] [19] ,主要包括构建流域河网、计算格网的汇流时间、计算格网响应函数、计算单元响应函数以及最终汇流计算。
NRF算法在流域汇流的模拟过程中,采用式(1)计算产流经过单个格网所需要的时间
。对于每个格网,根据格网流向,可以查找该格网产流流向流域出口的唯一路径,累加产流经过该路径上的所有格网所需的时间即可得到该格网的汇流时间t。
(1)
(2)
式中:
为产流从第i个格网流到下一个格网所需的时间,tan(ci)为相应的坡度,c0为临界坡度,小于临界坡度的格网计算汇流时间时,坡度均按照临界坡度计算,以避免在平原地区汇流时间无限长的情况发生。v45为坡度是45˚的格网中的平均波速,该值在模型计算中取4~10 m/s,并需要通过实测流量进行率定。针对每一个格网,其汇流是一个多天的组合过程,采用对流弥散方程作为相关方程:
(3)
本文在使用Hydro1k数据集的情况下,1 km的长度对于河道长度而言非常小,对于理想产流,有如下边界条件:
(4)
(5)
Qc的解为:
(6)
式中:erfc为误差函数,Qc为单位宽度内的径流量(m2/s),c为波速(m/s),t为时间(s),x为距离(m),I0为单位宽度内的入流量(m2/s)。
在24小时连续入流的条件下,出流为时间偏移量为0和24 h的结果相减,如式(7):
(7)
进一步求得时间尺度为日的格网响应函数,如式(8):
(8)
式中:t为径流产生后的时间,td为径流产生后的天数,PRF为格网响应函数。
根据计算所需空间尺度,将流域划分为若干单元。然后将每个单元中所有格网对应的格网响应函数整合转化为如下的单元响应函数,整合方法为直接线性平均,如式(9):
(9)
式中:n是单元中格网的数目,CRF为单元响应函数。
完成上述计算工作之后,根据单元响应函数和时间步长为日的径流输入,得到最后流域的河网响应函数:
(10)
式中:m是单元的个数,Qj为第j个单元的产流。
NRF汇流算法,提升了运算精度,简化了运算量,且汇流时间具有与高分辨网格推求出汇流时间同样的精度与稳定性,能够实现高效快速的汇流计算。但公式(1)没有考虑在不同流域下垫面影响下,坡度对流速影响程度是不同的。在部分流域运用式(1)和式(2)计算所得汇流时间过长,明显不符合实际,并导致径流模拟结果纳西效率系数极低。
3.3. NRF汇流方法改进
为了使得模型汇流算法原理更加合理并能够运用于不同流域。本文参照基于DEM的等流时线法的汇流时间 [16] 计算,将原程序中的相应计算公式改为如下公式:
(11)
式中:b为幂指数,反映坡度对流速的影响程度。当b为零时,表示所有全流域的网格都保持均匀流速,不受坡度的影响。改进后,模型汇流参数为b和v45,二者一起参与率定。汇流模块其它步骤与方程保持不变。汇流方法改进前后,汇流模块所用参数如表3。

Table 3. A list of parameters for routing module before and after improvement
表3. 汇流方法改进前汇流参数汇总表
4. 结果分析和讨论
本文分别以湘江流域的甘溪水文站、雅砻江流域的雅江水文站以及汉江流域的白河水文站为控制站点来测试汇流模块改进前后模型径流模拟效果。用纳西效率系数作为目标函数来进行模型参数优化。参数优化分为两步,首先用蒙特卡洛法优选出汇流参数。然后用优化算法CMAES寻找最优产流参数集合。其中产汇流单元空间尺度选择0.5˚ × 0.5˚空间格网。每个站点均采用11年的径流数据。模型率定期为7年,其中预热期1年,检验期为4年。
4.1. 汇流方法改进前后模型径流模拟结果比较
汇流模块改进前后模型产流参数的初始范围相同,如表4所示。汇流模块改进前后模型汇流参数及其初始值见表5。

Table 4. Initial calibration range of runoff generation parameters
表4. 产流参数初始率定范围

Table 5. Initial calibration range of routing parameters before and after improvement
表5. 汇流方法改进前后汇流参数初始值
汇流模块改进前后模型日径流模拟在检验期和验证期的纳西效率系数与径流总量相对误差系数如表6所示。
由表6可知,对比模型汇流方法改进前后,三个研究流域长系列日径流模拟的纳西效率系数都有不同程度的提高。汇流方法改进后,三个水文站点对本站点径流均有一个较好的模拟。图3到图5分别展示以上三个流域检验期单年的径流模拟结果,由日径流序列可以看出三个流域的径流特点不同。在各流域取得最佳日径流模拟效果时,产汇流参数优化结果见表7。

Table 6. Calibration and validation of study area before and after improvement
表6. 程序改进前后各流域模拟结果

Table 7. Optimal parameter of the model after improvement
表7. 程序改进后湘江流域及其子流域参数优选结果

Figure 3. Daily observed and simulated discharges at Ganxi basin in 2008
图3. 甘溪站控制流域检验期径流模拟结果

Figure 4. Daily observed and simulated discharges at Yajiang catchment in 2006
图4. 雅江站控制流域检验期径流模拟结果

Figure 5. Daily observed and simulated discharges at Beihe catchment in 1988
图5. 白河站控制流域检验期径流模拟结果
4.2. 汇流时间变化分析
甘溪站、雅江站、白河站流域在汇流方法改进前后,模型优化得到最优汇流参数时的流域格网汇流时间等值线分布分别如图6所示。由图分析可知汇流方法改进前后流域格网汇流时间空间分布图的大致规律都是靠近流域出口控制站的格网汇流时间较短,远离流域出口站的格网汇流时间较长;但受到地形影响,格网汇流时间等值线并非呈现规律环形分布,在一些山脉处,由于山脉左右两边格网汇流路径截然不同,山脉两边格网汇流时间相差较远,在山脉处会出现等值线密集的情况;对于相同格网,汇流方法改进前后计算所得汇流时间后者短于前者。由图6可知,在研究区域内,汇流方法改进后,等值线之间的间距相比汇流方法改进之前更加均匀。改进后的汇流方法计算所得的汇流时间空间分布合理。


Figure 6. Distribution of delays times for study areas
图6. 研究区域格网汇流时间空间分布图
为进一步分析空间地理特征对汇流时间的影响,分别计算了三个流域的形状系数、河网密度和平均坡度等空间地理特征,如表1所示。雅江站流域形状系数为5.21,在三个研究区域内最高;河网密度为0.09,在三个研究区域内最小;流域形状为狭长型,水系特征为羽状水系,因此流域汇流所需时间较长。而白河站和甘溪站流域形状介于狭长型和扇形之间,河网特征为混合水系,汇流时间相比于雅江站流域较快。对于甘溪站流域,计算所得流域汇流时间由9.42天变为1.36天。对于雅江站流域,计算所得流域汇流时间由44.78天变为6.50天。对于白河站流域,计算所得流域汇流时间由17.72天变为2.94天。这和模型率定得到的汇流参数b都小于汇流方法改进前的默认值0.5相符。参数b越小,说明坡度对流速的影响程度越小,产流经过不同坡度格网的时间差距越小,径流汇流时间缩短。
5. 结论
半分布式日尺度WASMOD模型原汇流算法仅考虑了汇流流速的空间变异性,但没有考虑流域下垫面因素对流速的影响程度。本文基于DEM的等流时线法与原汇流方法结合,增加了汇流参数b,即代表流域下垫面以及地形地貌因子坡度对流速的影响程度的幂指数,大大增加了原模型对不同流域和尺度的适应性。
将汇流模块改进前后的半分布式日尺度WASMOD模型应用于湘江、雅砻江及汉江流域,并以甘溪水文站、雅江水文站以及白河水文站为控制站点进行改进前后的对比分析。结果显示,汇流模块改进后,各控制站点的日径流模拟中的纳西效率系数均有不同程度的提高,其中甘溪站和白河站的结果有显著提高。模型汇流方法改进后纳西效率系数能够满足需求。三个流域的地形特点、土壤质地、气候条件、径流特点均不同,但改进后的模型在三个流域均有良好的适用性,说明改进后的模型具有普适性。
改进后的汇流算法在不同程度上缩短了模型汇流方法改进前计算所得的不合理的汇流时间,使得汇流算法更加合理,同时保留了原汇流算法的优势。结果表明将基于DEM的等流时线法与原汇流方法Network Response Routing汇流方法相结合进而改进模型是有效的。模型汇流方法改进后增强了半分布式日尺度WASMOD模型的径流模拟效果和适用性,利于之后WASMOD模型更广泛的应用。
参考文献