1. 引言
多属性决策是决策系统中的一个重要组成部分。它是指在考虑各种相互关联的因素下,从有限个备选的方案中,挑选出使决策者满意的方案的过程。关于多属性决策问题的研究,一直是备受人们关注的方向。由于人们思维的不确定性和模糊性,所掌握的决策信息的有限性,对现实中复杂的决策问题,人们很难做出准确的决策。结合模糊数学的知识,美国加州大学伯克利分校的教授Zadeh [1] 将模糊集引入到决策问题中,对决策理论进行了拓展和补充。很多学者对模糊集在多属性决策中的应用做了更深入的研究,对模糊集进行了推广和发展。保加利亚学者Atanassov [2] 提出了直觉模糊集的概念。之后,模糊集更多的拓展形式得以提出,如区间直觉模糊集 [3] 、模糊多重集 [4] 、2型模糊集 [5] 等。针对具有犹豫偏好的问题,Torra [6] 拓展了模糊集理论,提出了犹豫模糊集的概念。此后,很多学者据此做了大量的研究工作。徐泽水和夏梅梅 [7] 给出了犹豫模糊集数学符号化的表达,并提出了犹豫模糊集的信息集结算子,并将其运用到多属性群决策问题中。Torra和Narukawa [8] 将模糊集的一般运算法则拓展到犹豫模糊集中来,定义了犹豫模糊集的运算规则。
由于人们思维的局限性和不确定性,在诸多决策过程中,人们无法对某些决策信息给出精确的数值表示,只能以定性的方式加以描述。例如,当人们评价一个公司的组织构架的合理程度时,可以用“很好”、“好”、“一般”、“差”或“很差”来表示。与数值形式相比,诸如“好”、“一般”和“差”的语言表达,更加符合人们的思维方式和对事物的认知。因此,对于以语言形式给出决策信息的多属性决策问题受到了人们的高度重视。随着人们对语言形式的多属性决策问题研究的深入,相关的理论知识得到了极大的丰富。Rodriguez等 [9] 从提高语言描述的合理性和有效性出发,提出了犹豫模糊语言术语集的概念。为了刻画人们在决策过程中的犹豫性,在语言术语集的基础上,结合犹豫模糊集,Lin [10] 提出了犹豫模糊语言集的概念。Xu [11] 提出了不确定语言变量的概念。结合犹豫模糊集和不确定语言变量,Lin [10] 对犹豫模糊语言集进行了拓展,定义了犹豫模糊不确定语言集的概念,并提出了一系列的信息集结算子。Zheng [12] 提出了犹豫模糊不确定语言加权平均算子,用来集结决策信息,并在评估大学英语教师的专业发展能力问题上得到了很好的应用。Huo和Zhou [13] 考虑到评价指标之间的关联性,提出了犹豫模糊不确定语言算术相关平均算子和几何相关平均算子,很好地解决了建筑项目风险评估问题。Yang等 [14] 提出了新的犹豫模糊不确定语言加权平均算子和几何平均算子,将其运用到高等教育教学质量的评估问题中。Zhao等 [15] 结合拓展的犹豫模糊不确定语言加权几何集结算子,提出了一种新的多属性决策方法,用来解决我国纺织企业资源整合能力评价问题。Wei [16] 拓展了犹豫模糊不确定语言,提出了区间值犹豫模糊不确定语言,并定义了一系列区间值犹豫模糊不确定语言集结算子,丰富了犹豫模糊不确定语言的概念。
现有的关于犹豫模糊不确定语言决策问题的研究均存在着一些不足。比如定义犹豫模糊不确定语言得分函数或精确函数时存在不合理的例子。已有的相关文献多集中在犹豫模糊不确定语言集结算子的研究领域,对经典的决策方法的使用较少。在当下的多属性决策问题中,群决策更科学合理,而现有的基于犹豫模糊不确定语言信息的研究大多数集中在单人决策问题中。
本文主要探讨在犹豫模糊不确定语言环境下TOPSIS方法在多属性决策问题中的实际应用。在梳理分析模糊理论、信息集结和排序方法等基本知识的基础上,结合Choquet积分和Shapley值,定义了犹豫模糊不确定语言元的得分函数和精确函数,给出犹豫模糊不确定语言元的排序规则。为了全面地反映决策者在决策过程中相互影响、相互作用的特征关系,提出了犹豫模糊不确定语言Shapley Choquet积分算术平均算子(Hesitant fuzzy uncertain linguistic Shapley Choquet averaging operator,简称HFULSCA)和犹豫模糊不确定语言Shapley Choquet积分几何平均算子(Hesitant fuzzy uncertain linguistic Shapley Choquet geometric operator,简称HFULSGA)。最后,将文中提出的犹豫模糊不确定语言环境下TOPSIS方法应用到指导江西省城市地下综合管廊建设试点城市选择的问题中,为试点城市选择的决策问题提供一条新的思路。
2. 预备知识
2.1. 语言变量和不确定语言变量
美国加州大学伯克利分校教授Zadeh [17] 率先提出了语言变量的概念,用语言变量作为表示决策信息的有效工具,使得人们在决策的过程中可以更加方便和直接的表示个人的观点。若
表示可能的语言变量值,
是一个正整数,则一个语言术语集就可以表示为
。例如,可以将一个包含七个语言变量的语言术语集
表示为
。
定义2.1: [11] 对于一个语言变量
,其中
,
和
分别表示语言变量的上界和下界,则可称语言变量
为不确定语言变量。
若
为不确定语言变量集。考虑任意三个不确定语言变量
,
和
,则其一般的运算定义如下 [11] :
1)
;
2)
,其中
;
3)
;
4)
,其中
;
5)
,其中
。
2.2. 犹豫模糊不确定语言集
定义2.2: [10] 设
是一个论域,对于任意给定的不确定语言变量,则犹豫模糊不确定语言集可以定义为
(2.1)
其中,
,
是一些取值在区间
上的数值的集合,表示元素
隶属于不确定语言变量
的程度。为了方便讨论,将
称为犹豫模糊不确定语言元,其中,
且
。在这里,犹豫模糊不确定语言集
可以视作所有的犹豫模糊不确定语言元的集合。
定义2.3: [10] 设
和
为任意两个犹豫模糊不确定语言元且
,则有关犹豫模糊不确定语言元的一些运算规则可以定义如下:
1)
;
2)
;
3)
;
4)
。
本文定义了犹豫模糊不确定语言元的得分函数和精确函数,用来对犹豫模糊不确定语言元进行排序。
定义2.4:设
是一个犹豫模糊不确定语言元,则其得分函数可以定义为
(2.2)
其中,
是
中所包含的元素的个数。
定义2.5:设
是一个犹豫模糊不确定语言元,则其精确函数可以定义为
(2.3)
其中,
是
中所包含的元素的个数,
且
表示
在
上的一种置换,通过置换使得
。
对于任意两个犹豫模糊不确定语言元
和
,
1) 如果
,则称
优于
,也即是
;
2) 如果
,则
i) 如果
,则
;
ii) 如果
,则意味着
和
描述了同样的信息,也即是,
。
2.3. 模糊测度和Choquet积分
定义2.6: [18] 设
为论域。模糊测度被定义为有限集合
上的集函数,且满足如下性质:
1)
,
;
2) 如果
且
,则
,其中,
为论域
的幂集。
定义2.7: [19] 设
是论域
上的正真值函数,
为集合
上的模糊测度,则对于每一个模糊测度
,正真值函数
的离散Choquet积分为
(2.4)
其中,
表示
的一个置换,使得
,且
,
。
尽管在定义2.7中,Choquet积分可以反映元素之间的相互作用的关系,但是它却含有一定的局限性,即其仅仅考虑了“相邻的”两个元素
和
之间相互影响的特性。包含组合元素联盟的全面反映了元素间相互作用的现象,在Choquet积分中没有得到体现。
为了克服上述局限,更全面地反映元素间相互作用的特性,Marichal [20] 提出了广义的Shapley值
,
。 (2.5)
其中,
为
上的模糊测度,
,
和
分别表示
,
和
的基数。
根据式(2.5)的启发,Meng [21] 提出了在
上的含有
模糊测度
的广义的Shapley值,即
,
。 (2.6)
根据式(2.6),如果
,则
,
。 (2.7)
式(2.6)可以视为全面反映元素组合联盟
相互作用关系的期望值,其中的每一个联盟都属于集合
。特别地,式(2.7)可以视为全面反映元素组合联盟
相互作用关系的期望值,其中的每一个联盟都属于集合
。
基于定义2.7,Meng [21] 定义了包含
-Shapley Choquet积分的广义算术平均算子和几何平均算子,分别是
(2.8)
和
(2.9)
其中,
表示
的一种置换,使得
,且
,
。
3. 犹豫模糊不确定语言多属性群决策方法
本节主要介绍犹豫模糊不确定语言Shapley Choquet算术平均算子(HFULSCA)和犹豫模糊不确定语言Shapley Choquet几何平均算子(HFULSCG)及其相关的一些性质。之后,将会介绍用于度量犹豫模糊不确定语言集距离的距离测度,即基于Shapley Choquet积分的汉明距离。最后,在以上研究的基础上,提出在犹豫模糊不确定语言环境下的TOPSIS多属性决策方法,为之后的实证分析提供理论支持。
3.1. Shapley Choquet积分算子
定义3.1:设
为犹豫模糊不确定语言集,
为论域
上的
-模糊测度,则
的犹豫模糊不确定语言Shapley Choquet算术平均算子可表示为
(3.1)
其中,
表示
的一个置换,使得
,且
,
。
定理3.1:设
为犹豫模糊不确定语言集,
为论域
上的
-模糊测度,则利用犹豫模糊不确定语言Shapley Choquet算术平均算子对决策信息进行集结,所得的结果仍然是一个犹豫模糊不确定语言元,即
(3.2)
其中,
表示
的一个置换,使得
,且
,
。
定义3.2:设
为犹豫模糊不确定语言集,
为论域
上的
-模糊测度,则
的犹豫模糊不确定语言Shapley Choquet几何平均算子可表示为
(3.3)
其中,
表示
的一个置换,使得
,且
,
。
定理3.2:设
为犹豫模糊不确定语言集,
为论域
上的
-模糊测度,则利用犹豫模糊不确定语言Shapley Choquet几何平均算子对决策信息进行集结,所得的结果仍然是一个犹豫模糊不确定语言元,即
(3.4)
其中,
表示
的一个置换,使得
,且
,
。
3.2. 犹豫模糊不确定语言集的距离测度
结合Shapley Choquet积分,本小节中提出了犹豫模糊不确定语言集的距离测度,用以测量任意两个犹豫模糊不确定语言集的距离,为之后提出的多属性决策TOPSIS方法奠定基础。
定义3.3:设
和 为任意的两个犹豫模糊不确定语言元,则其汉明距离可以定义为
为任意的两个犹豫模糊不确定语言元,则其汉明距离可以定义为
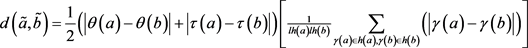 。 (3.5)
。 (3.5)
进一步分析研究,结合Shapley Choquet积分,本文给出了基于Shapley Choquet积分的犹豫模糊不确定语言集的汉明距离。
设论域为 ,两个犹豫模糊不确定语言集
,两个犹豫模糊不确定语言集 和
和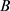 ,分别由两组犹豫模糊不确定语言元
,分别由两组犹豫模糊不确定语言元 和
和 构成,
构成, 为论域
为论域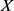 上的Shapley模糊测度,则犹豫模糊不确定语言集
上的Shapley模糊测度,则犹豫模糊不确定语言集 和
和 的基于Shapley Choquet积分的汉明距离可以表示为
的基于Shapley Choquet积分的汉明距离可以表示为
 (3.6)
(3.6)
其中, 为犹豫模糊不确定语言元之间的距离,可以由式(3.5)计算得出。
为犹豫模糊不确定语言元之间的距离,可以由式(3.5)计算得出。 是关于
是关于 上的
上的 的一个置换,以使得
的一个置换,以使得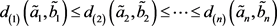 ,且
,且 ,
, 。
。
3.3. 基于Shapley Choquet积分的群决策TOPSIS方法
3.3.1. 问题描述
考虑一个犹豫模糊不确定语言环境下的群决策问题。设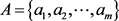 、
、 和
和 分别为方案集、属性集和决策专家集。方案
分别为方案集、属性集和决策专家集。方案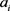 在属性
在属性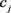 下的评价值以犹豫模糊不确定语言元
下的评价值以犹豫模糊不确定语言元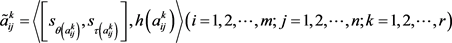 的形式给出。由此,可以得出犹豫模糊不确定语言决策矩阵
的形式给出。由此,可以得出犹豫模糊不确定语言决策矩阵 。另外,在实际决策中,决策专家和决策属性的权重信息一般是未知的,或者是部分已知的。在此,假设有关
。另外,在实际决策中,决策专家和决策属性的权重信息一般是未知的,或者是部分已知的。在此,假设有关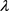 -模糊测度的信息是部分已知的,且用
-模糊测度的信息是部分已知的,且用 和
和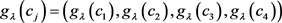 分别表示已知部分的决策专家和决策属性的
分别表示已知部分的决策专家和决策属性的 -模糊测度信息。
-模糊测度信息。
3.3.2. Shapley模糊测度的确定
如前所述,在多属性决策问题中,Shapley Choquet积分能够灵活地表示和处理属性间有相互作用、相互影响的问题,使决策过程更加合理,决策结果更加科学。本文使用离差最大化方法,通过构建数学模型来客观地确定决策问题中决策专家和决策属性的Shapley模糊测度。
1998年Wang [22] 率先提出了基于离差最大化的客观赋权方法,即在一个多属性决策问题,就决策属性而言,如果在某一个决策属性下,对于不同的方案,决策专家给出的决策属性值差异很小,则说明该属性无法很好地区分不同方案,从而该属性应该被赋予一个较小的权重。反之,属性应该被赋予较大的权重。
结合Shapley模糊测度,决策专家在属性 下针对不同方案所做出的评价值的总差异可以表示为
下针对不同方案所做出的评价值的总差异可以表示为
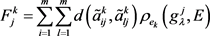 (3.7)
(3.7)
其中,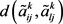 是
是 与
与 之间的汉明距离,可以由式(3.5)计算得到,
之间的汉明距离,可以由式(3.5)计算得到,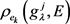 表示决策专家
表示决策专家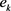 在属性
在属性 下的Shapley模糊测度。
下的Shapley模糊测度。
就所有的决策专家而言,在属性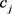 下某一方案和其他方案之间的总的评估偏差可以表示为
下某一方案和其他方案之间的总的评估偏差可以表示为
 。 (3.8)
。 (3.8)
为了确定在属性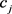 下,决策专家
下,决策专家 的
的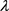 -模糊测度
-模糊测度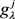 ,构建如下的数学模型:
,构建如下的数学模型:
 (3.9)
(3.9)
其中, 为决策专家
为决策专家 在属性
在属性 下的模糊测度的取值范围。
下的模糊测度的取值范围。
通过求解上述数学模型,可以得到在决策属性 下决策专家的
下决策专家的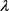 -模糊测度
-模糊测度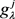 ,再根据式(2.6),即可计算得到在属性
,再根据式(2.6),即可计算得到在属性 下决策专家的Shapley模糊测度
下决策专家的Shapley模糊测度 。
。
对于决策属性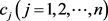 ,所有方案与其他方案的偏差可以定义为
,所有方案与其他方案的偏差可以定义为
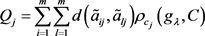 (3.10)
(3.10)
其中,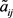 表示方案
表示方案 在属性
在属性 下,通过犹豫模糊不确定语言Shapley Choquet算术平均算子或者犹豫模糊不确定语言Shapley Choquet几何平均算子进行集结后的评价值,
下,通过犹豫模糊不确定语言Shapley Choquet算术平均算子或者犹豫模糊不确定语言Shapley Choquet几何平均算子进行集结后的评价值, 表示由式(3.5)计算得到的
表示由式(3.5)计算得到的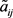 与
与 之间的汉明距离,
之间的汉明距离, 为属性集
为属性集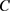 上的Shapley模糊测度。
上的Shapley模糊测度。
在属性 下,一方案与其他方案之间总的偏差可以表示为
下,一方案与其他方案之间总的偏差可以表示为
 。 (3.11)
。 (3.11)
为了确定在属性 下的
下的 -模糊测度
-模糊测度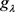 ,可以构建如下的数学模型:
,可以构建如下的数学模型:
 (3.12)
(3.12)
其中,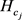 是属性
是属性 的模糊测度的取值范围。
的模糊测度的取值范围。
求解上述模型,可以得到在属性集 上的
上的 -模糊测度
-模糊测度 。再根据式(2.6),即可求得在属性集
。再根据式(2.6),即可求得在属性集 上的Shapley模糊测度。
上的Shapley模糊测度。
3.3.3. 基于Shapley Choquet积分的模糊多属性群决策TOPSIS方法
根据以上分析,利用离差最大化方法可以求得在多属性决策下专家集的Shapley模糊测度。然后,利用犹豫模糊不确定语言Shapley Choquet算术平均算子或者犹豫模糊不确定语言Shapley Choquet几何平均算子,可以将单个的多属性决策矩阵集结为综合的多属性决策矩阵。同时,结合离差最大化方法,通过构建数学模型,可以客观地求解得到属性集的Shapley模糊测度。最后,在犹豫模糊不确定语言环境下使用TOPSIS方法计算每个方案贴近度的取值大小,对方案进行排序。综上提出了基于Shapley Choquet积分的多属性群决策TOPSIS方法。具体步骤表示如下。
第一步,根据式(3.9),确定在属性 下决策专家集
下决策专家集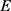 的
的 -模糊测度
-模糊测度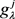 。
。
第二步,利用式(2.7),可以计算得到在属性 下的决策专家集
下的决策专家集 的Shapley模糊测度
的Shapley模糊测度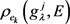 。
。
第三步,根据定义2.11提出的排序关系,确定在属性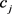 下的决策专家
下的决策专家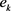 给出的以犹豫模糊不确定语言元
给出的以犹豫模糊不确定语言元 形式表示的评价值,然后,利用犹豫模糊不确定语言Shapley Choquet算术平均算子或者犹豫模糊不确定语言Shapley Choquet几何平均算子,将所有的个人决策矩阵
形式表示的评价值,然后,利用犹豫模糊不确定语言Shapley Choquet算术平均算子或者犹豫模糊不确定语言Shapley Choquet几何平均算子,将所有的个人决策矩阵 集结成综合的决策矩阵
集结成综合的决策矩阵 。
。
第四步,根据式(3.12),计算得到属性集 下的
下的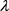 -模糊测度
-模糊测度 。
。
第五步,利用式(2.7),计算得到属性集 的Shapely模糊测度
的Shapely模糊测度 。
。
第六步,确定犹豫模糊不确定语言正理想解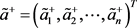 ,以及犹豫模糊不确定语言负理想解
,以及犹豫模糊不确定语言负理想解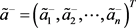 ,具体表示如式(3.13)和式(3.14)。
,具体表示如式(3.13)和式(3.14)。
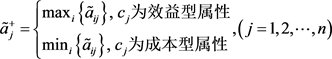 (3.13)
(3.13)
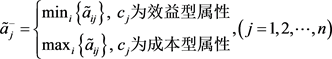 (3.14)
(3.14)
第七步,根据式(3.6),分别计算得到方案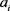 与犹豫模糊不确定语言正理想解
与犹豫模糊不确定语言正理想解 以及方案
以及方案 与犹豫模糊不确定语言负理想解
与犹豫模糊不确定语言负理想解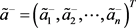 的汉明距离。
的汉明距离。
第八步,计算每一个方案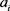 的相对贴近度
的相对贴近度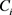 ,即
,即
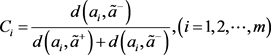 。 (3.15)
。 (3.15)
第九步,根据贴近度越大方案越优的原则,对方案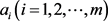 进行排序。
进行排序。
4. 犹豫模糊不确定语言TOPSIS法在城市地下综合管廊建设风险评估中的应用
以江西省开展城市地下综合管廊建设试点城市选择为研究背景,利用文中所提出的多属性群决策方法,对备选的试点城市的地下综合管廊建设风险进行评估,并对评估结果进行检验和对比分析,进而为最终的试点城市选择提供决策支持。
4.1. 问题描述
基于建设需要,江西省决定开展城市地下综合管廊建设试点工作,并对试点城市给予专项资金补助。本文将利用所提出的多属性群决策方法,对南昌 、九江
、九江 、赣州
、赣州 和上饶
和上饶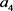 的城市地下综合管廊建设风险进行评估,并根据评估结果,为江西省城市地下综合管廊建设试点城市选择提供决策支持。基于第四章的内容,决定构建以政策支持力度
的城市地下综合管廊建设风险进行评估,并根据评估结果,为江西省城市地下综合管廊建设试点城市选择提供决策支持。基于第四章的内容,决定构建以政策支持力度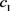 、施工管理水平
、施工管理水平 、资金支持力度
、资金支持力度 和社会影响
和社会影响 为风险评估的指标体系。现有
为风险评估的指标体系。现有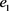 、
、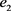 和
和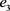 三位决策专家受邀,根据以上四个评价属性对涉及到的四个城市进行风险评估,且以犹豫模糊不确定语言作为评价值的评估结果构成决策矩阵,如表1、表2和表3所示。
三位决策专家受邀,根据以上四个评价属性对涉及到的四个城市进行风险评估,且以犹豫模糊不确定语言作为评价值的评估结果构成决策矩阵,如表1、表2和表3所示。
在决策过程中,关于 -模糊测度的信息是部分已知的,决策专家集在每一个决策属性下部分已知的
-模糊测度的信息是部分已知的,决策专家集在每一个决策属性下部分已知的 -模糊测度
-模糊测度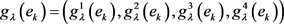 为
为


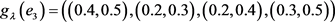

Table 1. Hesitant fuzzy uncertain linguistic decision matrix given by expert
表1. 专家 给出的犹豫模糊不确定语言决策矩阵
给出的犹豫模糊不确定语言决策矩阵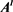

Table 2. Hesitant fuzzy uncertain linguistic decision matrix given by expert
表2. 专家 给出的犹豫模糊不确定语言决策矩阵
给出的犹豫模糊不确定语言决策矩阵

Table 3. Hesitant Fuzzy Uncertain Linguistic decision matrix given by expert
表3. 专家 给出的犹豫模糊不确定语言决策矩阵
给出的犹豫模糊不确定语言决策矩阵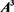
且部分已知的决策属性的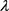 -模糊测度
-模糊测度 为
为 。
。
4.2. 城市地下综合管廊建设风险评估
基于上述的背景和问题描述,利用文中所提出的多属性决策方法,对江西省四个城市地下综合管廊建设风险进行评估。
第一步,根据式(3.9),构建如下的数学模型,用以求解属性 下决策专家集
下决策专家集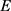 的Shapley模糊测度。
的Shapley模糊测度。
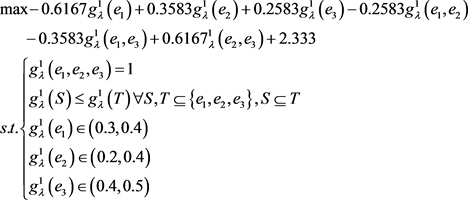
求解上面的数学模型,得到在属性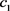 下决策专家集
下决策专家集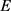 的模糊测度
的模糊测度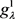 :
:
 ,
, 。
。
类似地,可以得到在属性 下决策专家集
下决策专家集 的模糊测度
的模糊测度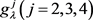 :
:
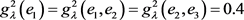 ,
, ,
,
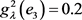 ,
,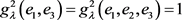 ,
, ,
,
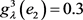 ,
, ,
,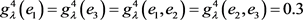 ,
,
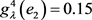 ,
,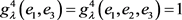 。
。
第二步,根据式(2.6),可以求解得到在属性 下的决策专家集
下的决策专家集 的Shapley模糊测度:
的Shapley模糊测度:
 ,
,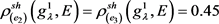 ,
,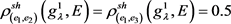 ,
,
 ,
, ,
, ,
, ,
,
 ,
, ,
, ,
, ,
,
 ,
,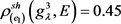 ,
, ,
, ,
,
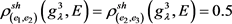 ,
, ,
, ,
,
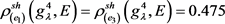 ,
, ,
,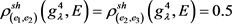 ,
,
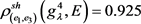 ,
, 。
。
第三步,利用由定义3.2给出的犹豫模糊不确定语言Shapley Choquet几何平均算子,通过对单个决策矩阵进行决策信息的集结,得到综合的决策矩阵 ,其中
,其中


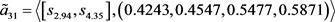





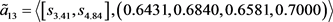


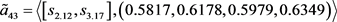
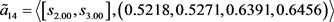


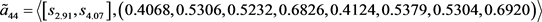
第四步,根据式(3.12),构建如下的数学模型,用以求解属性集 的Shapley模糊测度:
的Shapley模糊测度:
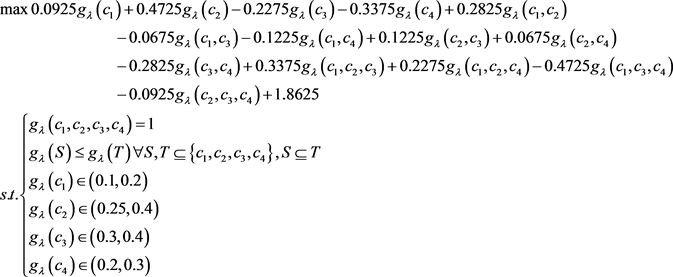
求解上面的数学模型,可以得到属性集 的模糊测度
的模糊测度 如下:
如下:
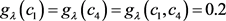 ,
, ,
,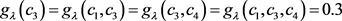 ,
,
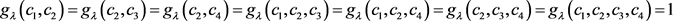 。
。
第五步,利用式(2.6),可以计算得到属性集的Shapley模糊测度如下:
 ,
, ,
, ,
,
 ,
,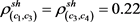 ,
, ,
,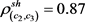 ,
,
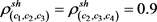 ,
,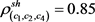 ,
, ,
,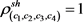 。
。
第六步,基于式(3.13)和式(3.14),可以得到犹豫模糊不确定语言正理想解 和犹豫模糊不确定语言负理想解
和犹豫模糊不确定语言负理想解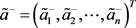 :
:
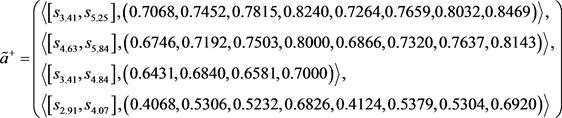
以及
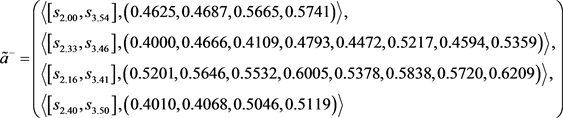 。
。
第七步,根据式(3.6),分别计算得到汉明距离 和
和 :
:
 ,
,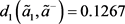 ,
, ,
, ,
,
 ,
, ,
, ,
,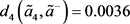 。
。
第八步,利用式(3.15),可以计算得到方案 的相对贴近度
的相对贴近度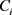 :
:
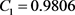 ,
,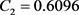 ,
,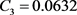 ,
, 。
。
第九步,根据计算得到的方案 的相对贴近度
的相对贴近度 的值的大小,对方案进行排序,可以得到
的值的大小,对方案进行排序,可以得到 。
。
根据以上的求解结果可知,与九江市、赣州市和上饶市相比,南昌市进行城市地下综合管廊建设的风险最小,可以作为江西省开展城市地下综合管廊建设工程的试点城市。
另外,在上述过程的第三步中,如果使用犹豫模糊不确定语言Shapley Choquet算术平均算子对单个决策矩阵进行信息集结,最终所得的结果仍是 。即在这种情况下,南昌市仍然是四个备选的试点城市中,地下综合管廊建设风险最小的城市。
。即在这种情况下,南昌市仍然是四个备选的试点城市中,地下综合管廊建设风险最小的城市。
5. 结论与展望
本文在犹豫模糊不确定语言环境下,提出了基于Shapley Chouqet积分的多属性群决策TOPSIS方法,综合地考虑了各个元素之间相互作用的特性。所提出的多属性群决策方法最主要的贡献在于:
1) 定义了犹豫模糊不确定语言元的得分函数和精确函数;基于Shapley Chouqet积分,全面考虑各个相关元素之间每一个联盟的相互作用的特性,提出用于集结信息的犹豫模糊不确定语言Shapley Chouqet算术平均算子和犹豫模糊不确定语言Shapley Chouqet几何平均算子;之后定义了度量犹豫模糊不确定语言集之间距离的汉明距离公式。
2) 基于离差最大化方法,通过构建数学模型,分别求解决策专家集和属性集的Shapley模糊测度。
3) 将经典的TOPSIS方法拓展到犹豫模糊不确定语言环境中,提出了基于Shapley Chouqet积分的多属性群决策TOPSIS方法。
在未来的研究中,可以结合其他的模糊积分,对集结算子和多属性群决策方法进行探讨。此外,如何将其他经典的多属性决策方法拓展到犹豫模糊不确定语言环境下多属性决策问题中,也是非常有价值的。