基于逆变换ARIMA-GM组合模型对汇率的预测研究

Research on Forecasting Exchange Rate Based on ARIMA-GM Combined Model of Inverse Transform

摘要: 本文在逆变换拟合残差ARIMA模型的基础上，研究了逆变换ARIMA-GM组合模型对汇率的预测。为了显示改进后的优点，将其与单一模型预测进行了对比分析，研究结果表明，组合模型对汇率的预测精度更高。

Abstract: This paper is based on the inverse transform fitting residual ARIMA model. The inverse ARIMA-GM combination model is used to predict the exchange rate. In order to show the improved advantages, it is compared with a single model prediction. The results show that the combined model has higher prediction accuracy for exchange rate.

1. 引言

现如今，世界经济在不断发展，各国之间的交流与日俱增，而汇率的变动影响着彼此之间的经济贸易，因此如何预测未来汇率的波动成为了当今世界的一个很重要的研究点。

对于汇率的预测，很多学者也有了一定的研究，其主要有单种模型、组合模型这两种模型预测。而单种模型的预测存在一定的局限性，因此便开始研究组合模型的预测，最早的组合模型预测是在1969年时由Betas和Granger [1] 提出来的，即在一个研究问题上采用两种以上的预测方法进行研究，最近几十年，国内在组合预测研究上也有了一定的进展，例如唐小我等教授发表多篇关于组合预测的文章，如：《管理科学学报》 [2] 、《系统工程学报》 [3] 等学术期刊上，在这些文章中主要的思想大多是用最小方差及绝对误差准则来计算组合预测方法的权系数向量 [4] 。Makridakis and Winkler [5] (1983)假定各模型的解释作用相同且不随时间变化，对各个模型的预测结果做简单算术平均，即使用了等权组合预测模型。林怡人 [6] (2011)分别采用联立方程(Simultaneous Equations)模型、单积自回归移动平均(ARIMA)模型和广义自回归条件异方差(GARCH)模型对人民币/美元汇率走势进行预测分析，再结合三者的预测结果构建组合预测模型。

针对汇率的预测，有学者提出逆变换拟合残差ARIMA模型，在一定的程度上预测效果较好，因此，在此基础上，本文章也尝试运用逆变换ARIMA-GM组合模型对汇率进行预测，并与单种模型预测结果进行比较，实证表明，组合模型比各单一模型的预测精度要高。

2. 逆变换-ARIAM模型汇率数据建模

一般情况，在利用金融时间序列数据作预测时，很多时候都默认模型残差服从正态分布，但在实际情况时，大部分的残差都不服从正态分布，甚至也不服从任何的已知分布。由此，根据文献 [7] 可知，残差的分布函数可用经验分布函数代替，那么经验分布函数可以定义为

$F_n\left(x\right)\text{=}\{\begin{array}{ccc}0& x<x_i& \\ \frac{i}{n}& x_{\left(i\right)}\le x\le x_{\left(i+1\right)},& i=1,2,3,\cdots ,n-1\\ 1& x>x_{\left(n\right)}& \end{array}$ (1.1)

其中 $x_i,i=1,2,\cdots ,n$ 为残差序列。

由于经验分布无反函数，此时采用插值法进行插值得到的经验分布函数为

$e_t=x_t-{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\varphi }_i}{x}_{t-i}+{\displaystyle \underset{j=1}{\overset{q}{\sum }}{\theta }_j}{e}_{t-j}=x_t-{\mu }_t$ (1.2)

(1.2)式为插值后的经验分布函数。从下一节开始，我们采用其逼近反函数，用修正后的经验分布代替分布函数，结合逆变换的方法研究ARIMA模型，并以此来预测未来30天汇率的波动。

3. GM模型汇率数据建模

设原始的汇率时间序列为 $x^0=\left\{x^0\left(1\right),x^0\left(2\right),\cdots ,x^0\left(n\right)\right\}$ ，对该序列作一次累加生成运算，令其结果为

$x^1\left(k\right)={\displaystyle \underset{i=1}{\overset{k}{\sum }}{x}^0\left(i\right)},k=1,2,\cdots ,n.$ (2.1)

对于序列 $x^1$ ，由文献 [4] 可知其满足如下的微分方程。

$\frac{\text{d}{x}^1}{\text{d}t}+a{x}^1=b$ (2.2)

为了估计(2.2)式中的参数a，b，此时将(2.2)式进行离散化处理，其结果得

$\Delta \left(x^1\left(k+1\right)\right)+a{x}^1\left(k+1\right)=b,k=1,2,\cdots ,n-1$ (2.3)

其中 $\Delta \left(x^1\left(k+1\right)\right)$ 为新生成的数列 $x^1$ 在第k + 1时刻的累减生成，即

$\Delta \left(x^1\left(k+1\right)\right)=x^1\left(k+1\right)-x^1\left(k\right)=x^{\left(0\right)}\left(k+1\right)$ (2.4)

对于新生的数列背景值，本文章采用谭冠军 [8] 提出的在区间 $\left[k,k+1\right]$ 差值的方法，其结果为

$Z^1\left(k+1\right)=\frac{1}{2n}\left[\left(n+1\right)x^1\left(k\right)+\left(n-1\right)x^1\left(k+1\right)\right]$ (2.5)

在公式(2.5)中 $n$ 的值由文献 [8] 中的经验公式法给出，即

$n={\left({\displaystyle \underset{k=2}{\overset{N}{\sum }}{R}_k}\right)}^{\frac{1}{N-1}}+\left(N-1\right)$

其中N为原始时间序列的样本数， $R_i=x^{\left(1\right)}\left(k\right)/x^{\left(1\right)}\left(k-1\right),k=2,3,\cdots ,N$ 。

将(2.4)、(2.5)、带入(2.3)有

$\{\begin{array}{l}{x}^0\left(2\right)=a\left[-\frac{1}{2n}\left(\left(n+1\right)x^1\left(1\right)+\left(n-1\right)x^1\left(2\right)\right)\right]+b\\ x^0\left(3\right)=a\left[-\frac{1}{2n}\left(\left(n+1\right)x^1\left(2\right)+\left(n-1\right)x^1\left(3\right)\right)\right]+b\\ \cdots \\ x^0\left(n\right)=a\left[-\frac{1}{2n}\left(\left(n+1\right)x^1\left(n-1\right)+\left(n-1\right)x^1\left(n\right)\right)\right]+b\end{array}$ (2.6)

令

$\beta ={\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ 1& 1& \cdots & 1\end{array}\right]}^T$

其中 $\begin{array}{l}{a}_{11}=-\frac{1}{2n}\left(\left(n+1\right)x^1\left(1\right)+\left(n-1\right)x^1\left(2\right)\right)\\ a_{12}=-\frac{1}{2n}\left(\left(n+1\right)x^1\left(2\right)+\left(n-1\right)x^1\left(3\right)\right)\\ ⋮\\ a_{1n}=-\frac{1}{2n}(\left(n+1\right)x^1\left(n-1\right)+\left(n-1\right)x^1(n))\end{array}$

$Y={\left(\begin{array}{cccc}{x}^0\left(2\right)& x^0\left(3\right)& \cdots & x^0\left(n\right)\end{array}\right)}^T,\alpha ={\left(a,b\right)}^T$

那么(2.6)式可写成为

$Y=\beta \alpha$

接下来要求GM(1, 1)模型的预测具体计算表达式，其步骤与文献 [4] 求法相同，这里就不再论述，最终得到

$x^0\left(k+1\right)={\hat{x}}^1\left(k+1\right)-{\hat{x}}^1\left(k\right)=\left(x^{\left(0\right)}\left(1\right)-\frac{b}{a}\right)\left[1-e^a\right]e^{-ak}$ (2.7)

其中 $k=1,2,\cdots n,n+1,\cdots$ ，则公式(2.7)就是GM(1, 1)模型的预测形式。

4. 组合模型建立

最优组合预测是根据一定的准则构造目标函数，在一定的条件下求得目标函数的最大值或最小值，从而求得组合预测方法加权系数，最优组合方法一般可以表示成如下数学规划问题

$\begin{array}{l}\max \left(\min \right)Q=Q\left(l_1,l_2,\cdots ,l_m\right)\\ s_{.}t\{\begin{array}{l}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{l}_i=1}\\ l_i\ge 0,i=1,2,\cdots ,m\end{array}\end{array}$ (3.1)

其中 $Q\left(l_1,l_2,\cdots ,l_m\right)$ 为目标函数， $l_1,l_2,\cdots ,l_m$ 为单种预测方法的加权系数。

在这篇文章中，以预测绝对误差作为预测精度的衡量指标，则组合模型的权系数计算如下：

(1) 预测误差平方和的倒数方法 [4]

$l_i=\frac{E_{ii}^{-1}}{{\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{ii}^{-1}}},i=1,2,\cdots ,m$ (3.2)

由(3.2)式可知 ${\displaystyle \underset{i=1}{\overset{m}{\sum }}{l}_i}=1,l_i\ge 0,i=1,2,\cdots ,m$ ，其中 $E_{ii}$ 为第 $i$ 种单项预测模型的预测误差平方和，公式为

$E_{ii}={\displaystyle \underset{t=1}{\overset{N}{\sum }}{e}_{it}^2}={\displaystyle \underset{t=1}{\overset{N}{\sum }}{\left(x_t-x_{it}\right)}^2}$ (3.3)

(3.3)式中 $x_{it}$ 为第 $i$ 种预测方法在第 $t$ 时刻的预测值， $x_t$ 为真实序列 $\left\{x_t,t=1,2,\cdots ,N\right\}$ 第 $t$ 时刻的观测值， $N$ 表示时间长度， $e_{it}=\left(x_t-x_{it}\right)$ 为第 $i$ 种方法在第 $t$ 时刻的预测误差。

(2) 均方误差倒数方法 [4]

$l_i=\frac{E_{ii}^{-\frac{1}{2}}}{{\displaystyle \underset{i=1}{\overset{m}{\sum }}{E}_{ii}^{-\frac{1}{2}}}},i=1,2,\cdots ,m$ (3.4)

其中 $l_i,E_{ii}$ 与(3.2)同义。

此时，对于组合模型的建立，可设 $\left\{x_t,t=1,2,\cdots ,N\right\}$ 为一组预测真实序列，它存在 $m$ 种预测方法， $x_{it}$ 为第 $i$ 种方法第 $t$ 时刻的预测，则有

${\hat{x}}_t=l_t{x}_{it}+l_m{x}_{2t}+\cdots +l_m{x}_{mt},t=1,2,\cdots ,N$ (3.5)

(3.5)式中表示 ${\hat{x}}_t$ 为 $x_t$ 的组合预测。

5. 实证分析

本文选取新浪财经网2017年1月1日至11月1日美元兑日元的收盘价作为实证数据，以天为单位收集数据，共305个观测值，其中前275个作为训练样本，后30个作为测试样本，收益率 $r_t$ 定义为两时间间隔 $\Delta t$ 的收盘价的差分取对数 $r_t=\log \left(s_t\right)-\log \left(s_{t-1}\right)$ ，最后用274个数据构成序列并进行模型检验。

首先对原始数据进行统计描述并做作时序图(见图1)。由图1可以看出，原始序列是非平稳状态。其次对数据进行平稳化处理，此时需要对原始数据进行对数差分，进一步对处理后的数据进行BOX检验，可以看出结果p值接近于0，这说明序列之间存在相关性。进一步进行单位根检验。可以看出ADF检验结果p值为0.01，说明在显著性水平 $\alpha =0.05$ 的情况下，此时原始序列经处理之后已是平稳序列。将差

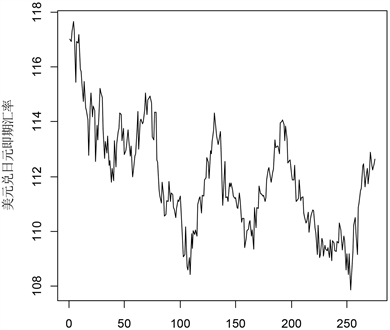
Figure 1. USD/JPY spot exchange rate sequence timing chart

图1. 美元兑日元即期汇率序列时序图

Figure 2. Sequential timing chart after USD/JPY spot exchange rate data logarithmic difference

图2. 美元兑日元即期汇率数据对数差分之后序列时序图

分之后的数据画出时序图(见图2)，由图也可以看出序列没有不平稳的迹象。

其次建立ARIMA模型，我们将用R语言代码获取模型的参数与模型指标，则可得ARIMA(1, 1, 1)模型为

$x_t=-0.0001+0.0151x_{t-1}+{\epsilon }_t+0.3151{\epsilon }_{t-1}$ (4.1)

在这篇文章中，分别采用时间序列ARIMA模型，逆变换方法改进的ARIMA模型，GM(1, 1)模型分别进行预测未来30天的数据，并用组合模型的方法进行预测，为考虑预测模型的有效性，分别以误差平方和(SSE)，均方误差(MSE)，平均绝对误差(MAE)，平均绝对百分比误差(MAPE)，均方百分比误差(MAPE)来衡量误差精度，其预测精度表如表1。由表1结果可以看出，在以预测误差平方和倒数、均方误差倒数权系数这两种方法构建的组合模型预测都比单种模型的预测误差要小，并且在两种权系数构建的组合模型中逆变换ARIMA-GM的预测效果都要比原始的ARIMA-GM组合模型的预测效果要好，说明逆变换ARIMA-GM组合模型预测能改进汇率预测的误差精度。

Table 1. Table of forecasting exchange rate error results for each combination model

表1. 各组合模型预测汇率误差结果表

6. 总结

在本文章中，采用逆变换残差拟合ARIMA模型，原始的ARIMA模型分别与GM(1, 1)模型进行组合，并利用组合模型对汇率进行预测，得到结果与原始的ARIMA模型、逆变换残差拟合ARIMA模型以及GM(1, 1)模型这几种单种模型预测结果进行比较，研究表明，组合模型的预测误差更小。经过本文章的研究也可以得到逆变换ARIMA-GM组合模型对汇率预测效果最佳的结论，从而验证了本文提出的方法对汇率预测的误差精度的改进具有一定的可行性。

基金项目

贵州省科学技术基金项目(No. 黔科合J字[2015]2076)，贵州省教育厅青年科技人才成长项目(No. 黔教合KY字[2016]168)，贵州民族大学科研基金资助项目(2017YB074)。

参考文献