摘要:
针对单相并网逆变器,基于传统的三相锁相环的闭环结构,文章提出了一种软件锁相环的实现方法。首先分析了锁相环的基本原理,推导了数学模型,在此基础上给出了该锁相环的软件设计方法。利用PSIM软件对电网电压幅值、频率和相位发生变化以及含高次谐波的影响做了仿真,结果表明该软件锁相环能有效、快速实现电网周期内任意时刻的锁相,不需等待电网过零点时刻的检测信号来锁相。分别采用TI公司的DSP TMS320F28035和TMS320F2808编程实现文中所提出软件锁相环的算法,并分别应用于500 W双通道单相光伏并网微逆变器和5 kW单相光伏并网逆变器中,结果表明所提出的软件锁相环能很好地实现电网电压相位的跟踪和频率的锁定,验证了所提出锁相环实现方法的正确性。
Abstract:
Based on the closed-loop structure of
traditional three-phase Phase-Locked loop, a software phase-locked loop (PLL)
is proposed for single-phase PV grid-connected inverter in this paper. The
operation principle of the presented phase-locked loop is analyzed and its mathematical
model is deduced. Also, the software implementation method of the phase-locked
loop is presented. Then, the influence resulted from the change of amplitude,
frequency and phase on the grid voltage is simulated by PSIM software. The
results show that the proposed software phase-locked loop can effectively and
quickly realize the phase tracking at any time in the cycle, without waiting
for the zero-crossing signal of the grid. The software phase-locked loop
proposed in this paper is respectively applied to DSP TMS320F28035 and
TMS320F2808 which belong to 500 W dual-channel single-phase PV grid-connected
micro-inverter and 5 kW single-phase PV grid-connected inverter respectively.
The results show that the proposed software phase-locked loop can achieve the
voltage phase tracking and frequency locking well, thus verifying the proposed
control method for single phase-locked loop.
1. 引言
随着新能源技术的发展,光伏并网逆变器进入了一个快速增长的阶段,对于并网电流的进网电流品质、相关标准都给出了严格的规定和限制。其中,并网逆变器的进网电流频率和相位必须与电网同步,这是满足并网标准的关键技术。然而,要保证进网电流能够精确、快速跟踪电网电压的相位和频率,锁相环(PLL, Phase Locked Loop)必不可少 [1] [2] [3] [4] [5]。
软件锁相较传统的硬件锁相,锁相速度快且不用搭建硬件电路 [6],可为并网逆变器节省成本。目前采用较多的PLL技术一般采用过零检测锁相法,虽然结构简单容易实现,但其动态性能不好,且对过零点电压要求比较高 [7],因此也限制了PLL的速度。文献 [8] 提到同时调频调相、多周期调节锁相方法,但这些方法只在电网电压过零点时,利用数字信号处理器(DSP, Digital Signal Processor)对电网过零点进行捕获,从而进行相位校正,不具有实时控制效果,另外占用了DSP中的3个定时器和2个捕获单元。文中提出一种单相并网逆变器软件PLL控制方法,在电网电压相位、频率和幅值发生变化时可有效、快速实现周期内任意时刻的锁相,而不需等待检测电网过零点,可有效实现并网电流与电网频率相位同步,程序代码简单,可移植性高。文中的方法通过PSIM软件仿真并运用在500 W双通道单相并网微逆变器和5 kW单相并网逆变器中,得到预期效果。
2. 软件PLL原理
2.1. PLL原理
文中借鉴三相PLL的闭环结构,提出单相软件锁相环架构,是通过构建两个虚拟的αβ正交信号来实现,其中令vα = vgrid,vβ = 0,再经过Park变换得到vd,vq [9] [10] [11] [12] [13],则:
(1)
θ表示锁相环得到的相位角,vgrid表示电网电压。
(2)
令电网电压
,其中Vgrid表示电网电压幅值,
表示电网电压相位,代入(2)式得到:
(3)
利用三角函数积化和差公式得到:
(4)
如(4)式,当锁相成功时,
则
,故若消除上式中的
,即控制
便可实现锁相。为此对vq求偏导得到如下(5)式,其中
。
(5)
 (6)
(6)
(7)
若系统稳定,则可近似认为
,整理(7)式得到:
(8)
将式(8)代入(4)式,得到如下所式且令:
(9)
如图1所示,将ωerr作为工频角速度误差送到PI调节器的输入端,PI调节器的输出为ωff,对ωff进行积分运算,可得到PLL的相位角输出量,PI调节器稳定控制后知ωerr等于零,即经锁相环得到了跟电网一致的工频角速度。图1中
表示锁相环以2π为一个周期输出相位角θ。
2.2. 软件PLL的实现方法
从PLL控制框图1可以看到,PI调节器的输出ωff需要进行积分运算,但在实际编程过程中,实现积分环节十分复杂。因角弧度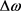 很小时存在
与
近似相等。因此具体实现时,可将电网周期N等分,从而得到固定的步进值
,在软件中断中叠加固定的弧度
来实现相位角的输出 [14]。如图2所示为相位叠加示意图。
很小时存在
与
近似相等。因此具体实现时,可将电网周期N等分,从而得到固定的步进值
,在软件中断中叠加固定的弧度
来实现相位角的输出 [14]。如图2所示为相位叠加示意图。

Figure 1. Control block diagram of phase-locked loop
图1. 锁相环控制框图
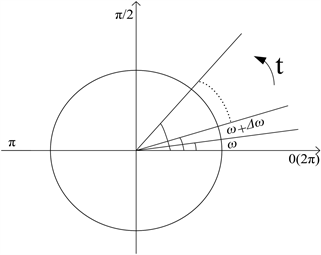
Figure 2. Schematic diagram of phase superposition
图2. 相位叠加示意图
如图3所示为PLL程序实现流程框图:
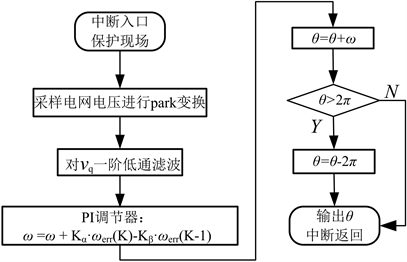
Figure 3. Program flow diagram of PLL
图3. PLL程序流程框图
vq对时间的微分在程序中是这样实现的:在s域,vq对时间的微分可以用
表示,对于
进行离散化可以得到如下式子:
(10)
其中fs为采样频率,进一步可以得到:
(11)
得到最终表达式:
(12)
在此基础上,程序中对其进行了一阶低通滤波:
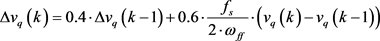 (13)
(13)
3. PLL仿真
3.1. 软件PLL仿真
为验证上述PLL控制方法的有效性,利用Power Simulation (PSIM)软件对文中的软件PLL方法进行仿真,仿真条件如下:电网幅值Vgrid = 314 V,电网频率f = 50 Hz,N = 400,ω = 2π/N = 0.0154 rad,采样频率fs = 20 kHz,文中提出的算法在仿真模块MCU中实现,将模块组合用来实现模拟电网的变化,如图4是为锁相环仿真电路图。
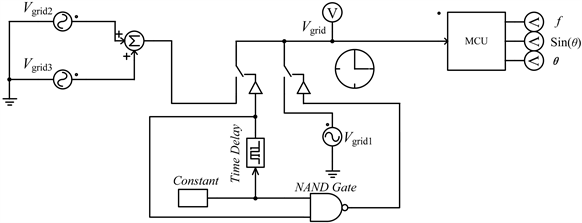
Figure 4. Simulation circuit diagram of the phase-locked loop
图4. 锁相环仿真电路图
电网幅值突变仿真波形如图5所示:在0.4 s时,电网从幅值314 V突变到200 V,到0.6 s时恢复正常,可以看到PLL输出与电网相位一致,实现准确锁相。实际50 Hz的电力系统,频率在49.42~50.42之间变化。电网频率突变仿真:频率在0.4 s时突变为48 Hz,在0.6 s时由48 Hz突变为51 Hz,波形如图6所示。
电网相位突变仿真:相位在0.4 s时滞后π/6,在0.6 s恢复正常,波形如图7所示,锁相环在一个电网周期内成功锁上。电网含高次谐波分量时仿真:在1 s时电网电压叠加高次谐波,波形如图8所示,锁相环相位输出没有受到影响,一直跟随电网电压相位,说明本软件锁相环还具有滤除高频谐波的作用。
文中提出的软件PLL控制方法经PSIM仿真验证,能在电网电压幅值,频率,相位突变时,能高效、快速实现锁相,同时本软件锁相环还具有滤除高频谐波的作用,更能保证逆变器并网时的安全性。为了更进一步验证文中提出的PLL控制算法在光伏并网逆变器系统里的可移植性,将此算法运用到双通道反激型并网微逆变器和H6桥型5 kW单相并网逆变器系统中,首先对PSIM软件对两种逆变器系统建模仿真,后通过相应的实验来验证 [15] [16]。
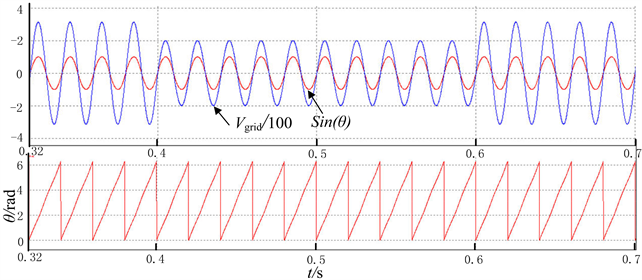
Figure 5. Simulation diagram of voltage mutation
图5. 电压突变仿真图
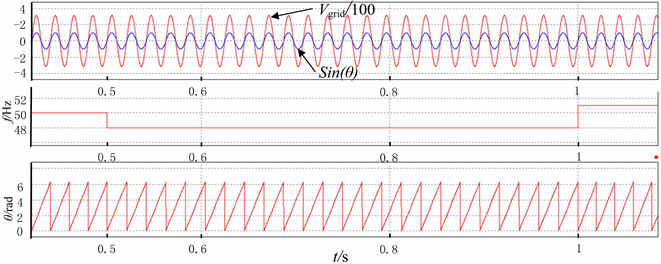
Figure 6. Simulation diagram of frequency mutation
图6. 频率突变仿真图

Figure 7. Simulation diagram of phase mutation
图7. 相位突变仿真图
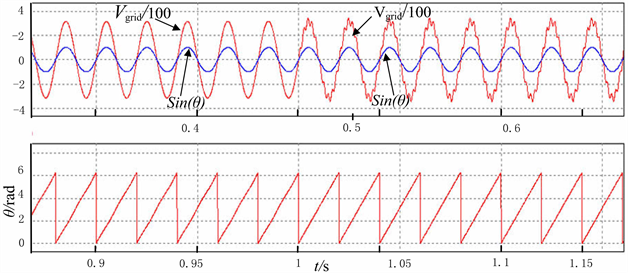
Figure 8. Simulation diagram of phase locking with high order harmonics
图8. 含高次谐波锁相仿真图
3.2. 双通道微逆变器的仿真实现软件PLL算法
微逆变器主电路仿真模型 [17] [18] 如下图9所示,图10为微逆变器输出电流和电网电压波形。为了方便显示,电网电压缩小了200倍。可以看到输出电流的相位可以很好地跟踪电网电压的相位,证明了文中提出的软件PLL算法可行性。
3.3. H6桥逆变器中的软件PLL算法
使用PSIM软件搭建H6桥型单相并网逆变器系统仿真模型如图11,仿真模型主要由光伏组件作为直流输入源,H6桥逆变器模块,电网模块及逆变器控制模块组成。对仿真模型仿真运行,得到系统仿真波形如图12所示。可以看到输出电流的相位可以很好地跟踪电网电压的相位,证明了文中提出的软件PLL算法可行性。
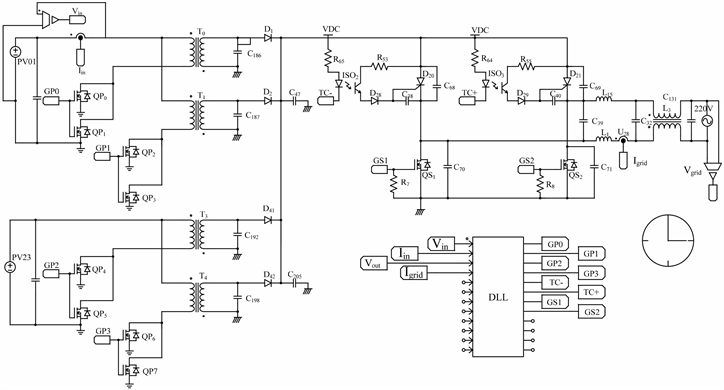
Figure 9. Micro-inverter system simulation model
图9. 微逆变器系统仿真模型
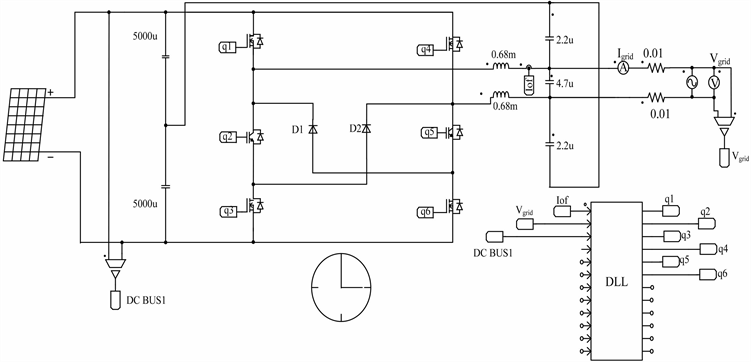
Figure 11. Single-phase grid-connected inverter system simulation model
图11. 单相并网逆变器系统仿真模型
4. 实验结果与分析
分别在500 W双通道微逆变器系统和5 kW单相光伏并网逆变器系统中使用文中的软件锁相环方法,前者采用TMS320F28035为主控芯片,后者采用TMS320F2808为主控芯片。电网频率由_IQ(15)表示,表示的最小精度为1/32768 = 3e−5。锁相程序放在50 μs的中断中,每次中断一次加角弧度
,ω = 0.0154 rad。通过配置DSP的CpuTimer0寄存器,得到想要的采样频率20 kHz,在中断发生以后,DSP进行如下步骤:使能A/D口对电网电压进行采样,进行park变换,通过PI控制器、积分部分的运算和输出步进角,然后等待下一次的中断。PI控制器的参数kα,kβ由仿真得到。如图13所示是利用调压器产生的电网电压测试锁相环控制效果,上位机显示的波形,其中
放大了100倍。图14是双通道微逆变器的实验样机,图15所示是500 W双通道微逆变器系统实际并网工作的波形,图16是5 kW单相光伏并网逆变器的实验样机,图17是实际并网工作的波形图。从两者的并网实验结果波形图可以看到并网电流与电网相位一致,实验结果表明软件锁相环能有效、快速地跟踪电网相位、频率,达到预期的控制效果,同时验证了文中提出的软件PLL程序算法的可移植性。

Figure 14. Experimental prototype of the dual-channel micro-inverter
图14. 双通道微逆变器的实验样机

Figure 16. Experimental prototype of the single-phase grid-connected inverter
图16. 5 kW单相并网逆变器样机
针对单相光伏并网逆变器的应用,文中提出一种新型软件锁相环的实现方法,在电网电压幅值、频率发生变化时可有效、快速、高精度实现周期内任意时刻的锁相,而不需等待检测电网过零点,可有效实现并网电流与电网锁相,提高了并网逆变器锁相精度和安全稳定性,省去了硬件电路,从而提高了并网逆变器系统的性价比,同时程序代码简单,可移植性高。在500 W双通道光伏微逆变器和5 kW单相光伏并网逆变器上验证了软件锁相环控制方法的正确性和锁相环程序代码的可移植性。
基金项目
国家自然科学基金资助项目(61873346);江苏省研究生科研与实践创新训练计划项目(SJCX17_0624);扬州市科技计划项目–产业前瞻与共性关键技术–共性关键技术研发(YZ2017013);扬州市科技计划项目–市校合作专项资金计划(YZ2018136)。