1. 引言
记
,
是实值函数。为方便,记
为
。考虑Kortewego-de Vries方程初值问题 [1] [2] [3]
(1)
其中
和
是常数。文献 [4] [5] 研究常微分方程的谱配置方法,文献 [6] 给出问题(1)的有界区域上混合问题的广义Jacobi逼近,文献 [7] 考虑了无界区域上三阶KdV方程(
)的Chebyshev-Hermite多项式时空谱配置方法,文献 [8] 提出了半无界区域上Fisher方程的Laguerre拟谱方法,文献 [9] 研究统计物理中无界区域上非线性Fokker-Planck方程的Hermite函数谱配点方法。考虑到问题(1)解的行波性态,为更好地吻合理论解在无穷远处的渐进行为,用含有因子
的插值函数逼近问题的理论解,利用高阶微分矩阵和一阶微分矩阵之间的关系处理高阶微分项,可以方便地构造非常简单的算法格式。
2. Lagrange插值函数及其微分矩阵
Hermite函数
定义为
其中
表示
阶Hermiter多项式。令
是
的根。以
为节点的Hermite函数谱配置方法的Lagrange插值基函数为 [6] [10]
对任意
,其Lagrange插值函数为
。对
求
阶导数得,
令
则由文献 [6] 中(3.68)和(7.93)
(2)
(3)
对那些解随
快速(或慢速)衰减的问题,用上述基函数不一定能得到高精度的数值误差结果。为了改进逼近精度,需要引入带伸缩因子的插值逼近,为此,给出下面的Hermite函数:
相应的Lagrange插值基函数为:
带松弛因子的微分矩阵记为
和(2)式类似有:
由
和(3)式知
阶微分矩阵:
3. Kortewego-de Vries方程的Hermite函数谱配置方法
3.1. 三阶Kortewego-de Vries方程配置方法
式(1)中令
和
可得三阶Kortewego-de Vries方程 [1] ,考虑初值问题:
(4)
用
,逼近式(4)的解
,将其代入式(4),得
(5)
式(5)等价于
(6)
令
,式(6)的矩阵形式为
(7)
这里矩阵
,为
矩阵,其元素为
显然,
是非线性项。
3.2. 数值结果
用格式(7)求解式(4)。在时间方向用步长为
的Crank-Nicolson格式离散式(7),得
(8)
由于式(7)式是关于
的非线性方程(或关于其分量的非线性方程组),实际计算时应用解非线性方程(组)的Newton迭代方法,需要计算迭代矩阵。为方便起见,用如下的迭代方法:在时间方向
这一层进行迭代:
(9)
设定迭代终止条件:对给定的
,如果
,即得
的值
。
三阶Kortewego-de Vries方程有精确孤波解 [1] [6] :
(10)
其中
和
是给定的参数。
用
-范数
度量数值误差。图1给出
和不同
,数值解和理论解的误差
的常用对数
随
的关系。可以看出,数值误差随
的增加及
的减小而快速衰减,空间方向达到谱精度;图2给出
和
误差,可以看出对较大的
所提算法格式仍然有效。
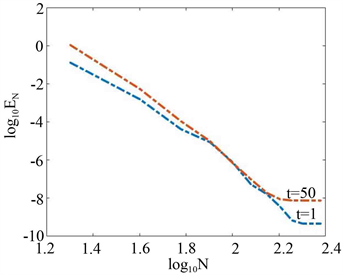
Figure 2.
图2.
3.3. 五阶Kortewego-de Vries方程配置方法
用
,逼近式(1)的解,将其代入式(1),得
(11)
和式(7)相似,式(11)的矩阵形式为
(12)
4. 数值结果
用格式(12)求解式(1)。在时间方向用步长为
的Crank-Nicolson格式离散式(12),得
(13)
由于式(13)式是关于
的非线性方程(或关于其分量的非线性方程组),用类似式(9)的迭代方法:在时间方向
这一层进行迭代:
(14)
设定迭代终止条件:对给定的
,如果
,即得
的值
。
式(1)有精确解 [11]
其中
和
是任意常数,
用
作为测试函数,用
度量数值误差。图3给出
和不同的
及
随
的变化关系。可以看出,数值误差随
的增加及数值误差
的减小而快速衰减,空间方向达到谱精度;图4给出
和不同的伸缩因子
数值误差
随
的变化关系,可以发现对适当小的
数值误差更小。但如何选取最佳伸缩因子是一个未解决的问题。
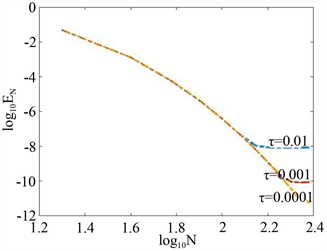
Figure 3.
图3.

Figure 4.
图4.
5. 结论
以带松弛因子的Hermite函数配置方法求问题(1) (三阶和五阶)的数值解,逼近无界区域上的KdV方程的理论解。由于基函数含有因子
,通过适当选取松弛因子
可以使数值解能更好地吻合理论解在无穷远处的渐进行为,所给算法尤其适合于非线性问题。
基金项目
国家自然科学基金项目(11371123);S201810464034。