1. 引言
众所周知,自同构群
是由群G决定的。反之,如果知道
的阶,能否确定群G的构造?余红宴和黄本文在这方面做了一些研究,见 [1] [2] [3] 。本文将讨论当
的阶为
时,群G的构造。文中设群G是有限Abel群,
表示群G的阶,
表示群G的自同构群,
表示n阶的循环群,而
表示群G的Sylow
子群,其它符号是标准的,见文献 [4] 。
2. 预备知识
引理2.1 [4] 若
,则
为
阶的交换群,其中
为欧拉函数。
引理2.2 [4] 若G是
阶交换群,则
。
引理2.3 [4] 设
,则当
时,
。
引理2.4 [5] 设G是
阶交换群,G的型为
,其中
,
,则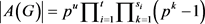 ,其中
,其中
下面在定理的证明中,总假定
为不同的奇素数。
3. 主要结果及证明
定理3.1设 为有限交换群,当
(p,q为互异的奇素数)时,群G最多有6型。
证明:设
,则
,并且
。由于对每个奇素数
来说,都有
,而
,则有
,所以
。
(1) 当
时,
。又
,而
,故
。
(I) 当
时,
,则
,进而
,与
矛盾。
(II) 当
时,
,则
,
。
(i) 若
,有
,与
矛盾。
(ii) 若
,有
,与
矛盾。
(2) 当
时,由于
,得
,则有
。又由
,而
,故
。
(I) 当
时,则有
,我们有
,
。由于
,可得
。当
为素数时,有
,
。
(II) 当
时,则
,
。
(i) 若
,有
,
。因为
,令
,即
。当
为素数时,有
,
。同理,令
,即
,当
为素数时,有
,
。
(ii) 若
,则有
,
,此时
,与
矛盾,故G不存在。
定理3.2设G为有限交换群,当
(p,q为互异的奇素数)时,群G最多有22型。
证明:设
,则有
,且
。由于对每一个奇素数
,有
,而且
,所以
,故
。
(1) 当
时,
。由于
,且
,可得
。
(I) 当
时,由定理3.1的证明可知,G是不存在的。
(II) 当
时,
,则
。
(i) 若
,有
。
(ii) 若
,有
。
(iii) 若
,有
。均与
矛盾。
(2) 当
时,
,由
可知,
,则
。
(I) 当
时,我们有
,并且
,故
。
(i) 当
时,有
,此时
,得出
。当
为素数时,有
,
。
(ii) 当
时,可知
。
(a) 若
,则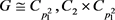 。由于
,若令
,即
。当
为素数时,有
,
。同理,令
,有
,
。
。由于
,若令
,即
。当
为素数时,有
,
。同理,令
,有
,
。
(b) 若
,则有
,而
,与
矛盾,因此G不存在。
(II) 当
时,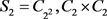 。
。
(i) 当
时,
。
(a) 若
,有
,由于
,可得
。当
为素数时,有
。
(b) 若
,有
,因为
,可令
,则有
。当
为素数时,有
。
(ii) 当
时,
。
(a) 若
,则有
。
若
,此时
。若令
,则
。当
为素数时,有
。同理,令
时,有
。
若
,由于
,得
,矛盾,故G不存在。
(b) 若
,此时
。
若
,由于
,则有
,此时得到
,与
为不同的奇素数矛盾,因此G不存在。
若
,由
,我们有
,矛盾,故G不存在。
(3) 当
时,
,又
,所以
。由
,可得
,
。
(I)
:
,此时有
。由于
是不同的偶数,而
,则当
为素数时,有
,
;当
为素数时,有
,
。
(II)
:此时只需考虑
。由于
,若令
,则有
。由于
是不同的偶数,而
,则当
为素数时,有
,
,
,
。同理,令
时,有
,
,
,
。
(III)
:只需考虑
,由
,可得
,与
为互异的奇素数不符,故G不存在。
定理3.3 设G为有限交换群,当
(p,q为互异的奇素数)时,群G最多有49型。
证明:设
,则有
,以及
。由于对每个奇素数
,有
,而
,所以
,因此可得
。
(1) 当
时,
。又因为
,而
,所以
。
(I) 当
时,由定理3.2的证明知,G不存在。
(II) 当
时,
,则
。
(i) 若
,则有
与
不符。
(ii) 若
,由计算可知均有
矛盾,故G不存在。
(2) 当
时,
,因为
,可知
,则
。
(I) 当
时,由于
,而又有
,故
。
(i) 当
时,
,此时
,得到
。当
为素数时,有
,
。
(ii) 当
时,可知
。
(a) 若
,有
,此时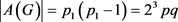 。若令
,即
。当
为素数时,有
,
。同理,令
时,有
,
。
。若令
,即
。当
为素数时,有
,
。同理,令
时,有
,
。
(b) 若
,则有
。由
,若
,
为偶数时,产生矛盾。
为奇数时,代入等式左边为偶数,右边为奇数,不符,因此G不存在。
(II) 当
时,
。
(i) 当
时,
。
(a) 若
,有
,由
,得出
。当
为素数时,有
。
(b) 若
,则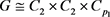 ,此时
。若
,可知
。当
为素数时,有
。
,此时
。若
,可知
。当
为素数时,有
。
(ii) 当
时,
。
(a) 若
,可知
。
当
,由
,得
。若令
,即
。当
为素数时,有
。同理,令
时,有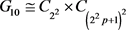 。
。
当
,由
,得
,产生矛盾,故G不存在。
(b) 若
,有
,
。
当
,我们有
,从而
。若令
,则
,于是有
。
当
,则有
,于是
,产生矛盾,因此G不存在。
(III) 当
时,
。当
时,由前面的证明易知G不存在,所以只需考虑
。
(i) 当
时,
,有
。由于
,可得
,从而
。当
为素数时,有
。
(ii) 当
时,
,同样也只考虑
,于是
,此时
,可得
。若令
,即
,当
为素数时,有
。同理,令
时,有
。
(3) 当
时,
,又因为
,所以
。由
,得出
,
。
(I) 当
时,
(i)
:此时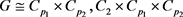 ,于是
。由于
是不同的偶数,而
。所以当
为素数时,有
,
;当
为素数时,有
,
;当
为素数时,有
,
;当
为素数时,有
,
。
,于是
。由于
是不同的偶数,而
。所以当
为素数时,有
,
;当
为素数时,有
,
;当
为素数时,有
,
;当
为素数时,有
,
。
(ii)
:只需考虑
,于是有
。由于
是不同的偶数,若
,则
,而
。所以当
为素数时,有 ,
,
,
;当
为素数时,有
,
,
,
。同理,若令
,则当
为素数时,有
,
,
,
;当
为素数时,有
,
,
,
。
,
,
,
;当
为素数时,有
,
,
,
。同理,若令
,则当
为素数时,有
,
,
,
;当
为素数时,有
,
,
,
。
(iii)
:我们只需考虑
,由
,可得
,
,则有
,
。
(II) 当
时,
。
(i) 当
时,
(a) 若
,有
,从而
,进而
。由于
是不同的偶数,而
。所以当
为素数时,有
;当
为素数时,有
。
(b) 若
,有
,从而
,进而
。若令
,则有
,而
。所以当
为素数时,有
。
(ii) 当
时,
(a) 若
,我们有
,从而
,进而
。若
,则
,而
。当
为素数时,有
,
;同理,若令
,则有
,
。
(b) 若
,有
。由于
,从而
。此时
,与
为互异的奇素数不符,故G不存在。
(iii) 当
时,
(a) 则
,于是
,可得
。此时
,与
为不同的奇素数矛盾,所以G不存在。
(b) 有
,此时
,从而可得
,矛盾,所以G不存在。
(4) 当
时,我们有
。
(I)
:此时
,从而
,而
。所以当
为素数时,有
,
。
(II)
:此时
,从而
。令
,而
,此时
,
,产生矛盾,因此G不存在。同理,
时,G也是不存在的。
(III)
:有
。由于
,此时得到
,与
为互异的奇素数不符,从而G不存在。
(IV)
:有
,此时
,产生矛盾,故G不存在。
4. 结束语
本文讨论了自同构群的阶为
的有限Abel群G的构造,得出:当t = 1时,G最多有6型;当t = 2时,G最多有22型;当t = 3时,G最多有49型。
基金项目
国家自然科学基金(11401424)资助项目资助。
参考文献