1. 引言
列车运行阻力主要由机械阻力和空气阻力组成,对于轮轨形式的高速列车,当运行速度超过300 km/h时,空气阻力可以达到的总阻力的75% [1]。根据Davis公式 [2] :列车的运行的机械阻力与速度的一次成正比,空气阻力与速度平方成正比,因此,随着列车运行速度的进一步提高,空气阻力的占比将越来越大,同时,传统轮轨列车由于车轮-轨道之间的轮轨关系限制,存在的临界运行速度 [3]。低真空管道磁浮列车是一种新型的交通运输系统,具有快速、环保、高效的特点 [4]。低真空管道磁浮列车系统将一定真空度的管道与磁浮列车相结合,实现列车在无轮轨阻力,低空气阻力,低噪声模式下高速运行。1904年, Robert Goddard首先提出在波士顿至纽约间建立一条真空管道铁路,磁浮列车在管道内的运行速度为1600 km/h [5] [6],1999年,Daryl Oster获得了真空管道运输系统的发明专利 [7],2013年,Elon Musk提出了超级高铁(Hyperloop)的计划方案 [8]。目前,全球已经掀起了真空管道高速列车研究的热潮。
周晓 [9] [10] 等基于不可压缩粘性流,对二维管道内的真空管道列车气动特性进行了研究。得到了真空管道内列车空气阻力的影响因素及相关影响规律。文章中的计算物理模型为不可压缩粘性流,由于管道运行列车的速度已经超过不可压缩的范畴,加之所采用的几何模型为二维模型,与真实列车有较大差别,因此,得到的结果是不够准确的。刘加利等 [11] [12] 基于三维可压缩粘性流,研究了管道压力、阻塞比等对列车气动阻力、噪声等的影响。文中所用到的模型未考虑列车底部与悬浮板的相互作用,因此,未考虑气动升力的变化规律。黄尊地等 [13] 对真空管道内运行列车的外流场算法进行了研究。得到了三维效应、压缩效应和非定常效应对列车外流场的影响。文中把计算模型分为静态模型和动态模型,分别用可压缩和不可压缩来计算真空管道内运行列车的气动特性,实际上,文中分析比较中采用的不可压模型和可压缩模型,静态计算和动态计算在问题的提出上就存在失当之处,如文中的动态算法把列车的波系解释成压缩波和膨胀波,这是对管道内列车运行环境的误解。因此,亟需对管道列车运行气动特性的进行解释。
本文从管道内磁浮列车流场的形成入手,着重于研究管道压力、阻塞比对于真空管道磁浮列车的气动特性影响。
2. 计算模型和网格
2.1. 计算模型
本文主要研究阻塞比、管道压力等因素对低真空管道磁浮列车的气动特性的影响规律,因此,对计算模型进行了适当简化,本文采用头车–中间车–尾车三编组形式的列车模型,其中头车尾车具有相同形状。整个车身做光滑处理,没有任何附属部件,计算模型如图1所示,列车头、尾车车长为28 m,中间车车长为25 m,三编组总长度包括车间间隙为82 m,列车底部与磁浮板的间距为20 mm,车身的最大断面面积为10 m2。进行管道面积变化时,保证车体和悬浮架参数不变,对管道面积按比例进行缩比。图1给出了本研究的计算模型。

Figure 1. The schematic diagram of computational model
图1. 计算模型示意图
2.2. 计算域与计算网格
计算域如图2所示,由于列车运行的速度在亚声速范围,为了减小计算区域对计算结果的影响,考虑网格量及计算精度,入口和出口设置在距离车鼻360 m远处,约为特征长度(车高)的90倍。整场采用结构化网格划分,图3为部分计算区域的网格图,壁面的第一层网格高度为10−5 m,增长比为1.2,保证壁面Y+在1的量级范围内,整场网格数量约为4500万。
3. 计算方法
由于涉及到低真空度范围内的计算,因此,需要考虑连续介质模型是否适合计算。在管道内,当管道的压力降低时,管道内空气的密度会降低,也即管道内的空气会越来越稀薄。通常用克努森数(Knudsen)表示空气的稀薄程度,当克努森数小于0.01时,气体流动属于连续介质的范畴。克努森数定义为分子平均自由程与流动特征长度的比值,其表达式为:
(1)
式中:Kn——克努森数,
——分子平均自由程,L——流动特征长度。
分子的平均自由程表达式为:
(2)
式中:
——玻尔兹曼常数,
,T——温度,d——分子直径,p——压力。
由(2)式可计算得到在管道压力在0.01 atm至1 atm时的分子平均自由程变化范围约为,取高速列车的高度为特征长度(通常约为4 m),则可以得到:
(3)
本文中,管道内的空气压力最小为0.01 atm,可见,本文的计算可以采用连续介质模型。
本文使用大型商业软件Fluent进行流场计算,控制方程为三维定常可压缩N-S方程,离散方法采用基于格心格式的有限体积方法,空间离散格式采用Roe格式,粘性项采用二阶中心差分格式,时间离散采用LU-SGS隐式离散方法,湍流模型为k-ωSST模型。
边界条件:由于真空管道内磁浮列车运行速度处于亚音速范围,因此,在计算域的入口和出口均采用无反射边界条件。为了模拟车体与管道,磁浮板的相对运动,设置管道、磁浮板与来流具有相等的速度。车体壁面为无滑移固定边界条件。
4. 计算结果及分析
本文首先分析低真空管道磁浮列车周围流场的流动特性,然后分别分析管道面积、管道压力对低真空管道磁浮列车气动特性的影响。本文中用到的管道面积、列车速度和管道压力会在分析影响规律时给出。
4.1. 低真空管道列车扰流的流场特性
由于列车是在密闭的管道内运行,不会近似于列车进出隧道产生压缩波和膨胀波的过程,可以近似于明线运行状态,所不同的是其周围有管道边界。不失一般性,这里以真空管道面积80 m2、列车运行速度600 km/h、管道压力位0.3 atm为例进行流场分析。
图4为列车头部的压力云图和纵剖面流线图,其中流线图的颜色深浅表示气流速度大小。可以看出:在列车头部附近,气流在流经鼻锥后被导向车顶和车底。图5给出了对称面上的速度图。可以看出:气流在接近列车鼻锥时逐渐减速,在鼻锥前端滞止为零,在列车鼻锥处形成驻点和高压区,气流流过鼻锥后,在车体表面形成边界层,远离边界层区域的气流由于流道的减小,速度逐渐加大,在车顶处达到最大。同样,流向鼻锥下方的气流也具有同样的趋势,如果来流的速度小于音速,不同管道面积,不同管道压力条件下,列车头部的流场均表现出同样的流动特征。

Figure 4. The train head pressure contours and the longitudinal profile streamlines
图4. 列车头部的压力云图和纵剖面流线图

Figure 5. Velocity contours on symmetry plane
图5. 对称面上的速度图
图6为列车尾部车体表面压力云图及对称面速度云图,气流从列车前部流向后部,边界层不断变厚,导致尾车车体上部边界层厚于头车,当气流到达尾车流线型部位时,由于流道面积的增大,气流的速度减小。图7为列车尾部流场的流线图,可以看出,由于列车在上部、侧向的压差,导致上部气流、侧向气流由于剪切作用形成了一系列的涡对。这些列车周围的局部流动特征与列车在明线运行时类似。

Figure 6. Pressure contours on the train tail and the velocity contours on symmetry plane
图6. 列车尾部压力云图及对称面速度云图
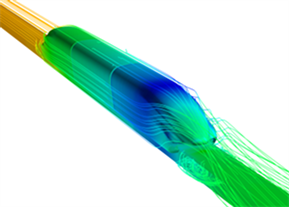
Figure 7. Streamlines in the tail flow field
图7. 尾部流场流线图
需要指出的是,上述流场特征是在真空管道内不出现激波时的。实际上,气流流经列车时,列车与管道形成的环状空间与拉瓦尔喷管相似,在不考虑列车的局部细节条件下,该环状空间可以近似于一维变截面的管道,管道内的流动符合一维定常等熵流动的特征,即具有膨胀加速或压缩减速的流动特性,收敛管道中的亚声速流动和扩张管道内的超声速流动是膨胀加速的,沿着管道流速不断增加,而压强、密度和温度不断减小;扩张管道中的亚声速流和收敛管道中的超声速流是压缩减速的,沿着管道流速不断降低,而压强、密度和温度却不断增加。下面以真空管道面积80 m2、列车运行速度1000 km/h、管道压力0.3 atm进行说明。
当列车运行速度达到1000 km/h时,其Mach数等于0.817,气流从入口到达列车后,由于管道面积的收敛,沿着管道流速不断增加,在扩张管道与收敛管道的交界处,此位置位于列车的尾车处,气流流速达到声速,在扩张管道,即在尾车的流线型后端气流进一步加速,达到了超音速,管道中出现了激波,激波在管道中的反射将进一步加剧管道中的流动条件,同时,由于激波的出现,尾车的气动特性也将发生很大的变化,通过改变背压的条件,改变尾车截面的变化率将会改变激波的强度,改善尾车的气动特性。因此对于低真空管道运行的磁浮列车,其头、尾车设计成非对称形式将有利于列车的气动性能(图8)。

Figure 8. Mach contours on symmetry plane
图8. 对称面马赫数云图
4.2. 管道面积对于列车气动特性的影响
当管道面积变化时,由于列车的截面面积保持不变,因而会导致管道内堵塞比变化。如果管道内出现激波,堵塞比的改变将导致激波位置、强度发生改变,气动性能也发生改变。
为了便于分析,定义无量纲系数即列车气动阻力系数和气动升力系数公式如下:
(4)
(5)
式中,
、
为列车空气阻力系数,
、
为列车空气阻力和升力,
管道内空气密度,
为列车运行速度,A为参考面积。
图9为管道内压力0.3 atm、速度分别为600 km/h、800 km/h、1000 km/h时阻力系数随管道面积的变化。从图中可知:当列车运行速度为600 km/h时,随着管道面积的减小,头车的阻力系数逐渐增大,中间车也表现了同样的趋势,而尾车在管道面积大于70 m2时,阻力系数很小,接近于零,变化也很小,但管道面积小于60 m2时,其阻力系数会随着管道面积的减小大幅增加。从头车、中间车、尾车的阻力系数来看,在管道面积大于60 m2时,三车的阻力系数大小排列为:头车 > 中间车 > 尾车。而当管道面积为40 m2时,尾车的阻力系数大于中间车的阻力系数。出现这种现象可能是在时速600 km下,管道面积为60 m2时。尾车周围的流动状态发生很大的改变,在尾车出现了激波所导致。当列车运行速度为800 km/h和1000 km/h时,三车的阻力系数大小排列为:尾车 > 头车 > 中间车,随着管道面积减小,阻力系数增大,三车的阻力系数随管道面积不如速度为600 km/h时变化剧烈。说明此时列车周围的流动状态是相似的。图10为管道内压力0.3 atm、速度分别为600 km/h、800 km/h、1000 km/h时三车升力系数随管道面积的变化。可见,尾车的升力系数要远远大于头车和中间车,而且,随着管道面积的减小,头车和中间车升力系数略微增加,而管道面积变化对于尾车的升力系数影响较大,特别是当管道面积小于某一临界值时,会出现尾车升力系数的剧增。图11给出了管道面积为80 m2,速度为800 km/h,管道压力为0.3 atm时对称面的Mach数云图,从图中可以看出,在列车的尾部出现了很明显的激波,可知在速度大于800 km/h时,列车的尾部将会出现激波。对照相应的阻力系数和升力系数,可以知道,当尾车出现激波后会引起尾车气动性能的剧烈变化。
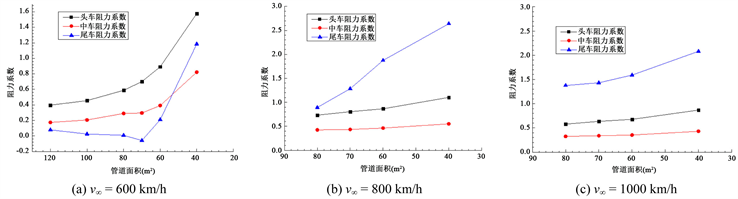
Figure 9. Coefficients of drag on tube area at different speed
图9. 不同速度下阻力系数随管道面积变化
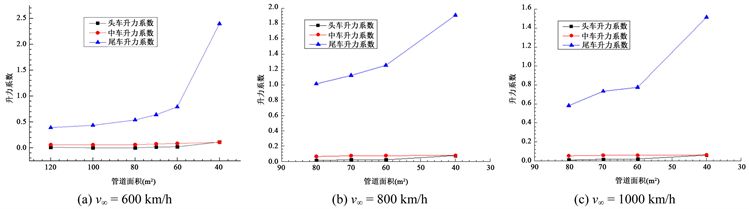
Figure 10. Coefficients of lift on tube area at different speed
图10. 不同速度下升力系数随管道面积变化
4.3. 管道压力对于列车气动特性的影响
衡量气体分子热运动的剧烈程度由温度来表现,气体分子运动越快,温度越高。管道内气体的压力是气体分子热运动作用的统计效应,当温度不变时、管道内的压力进行变化时,也即意味着管道内气体的密度发生了改变,根据Re的定义,可知,管道中气体的单位雷诺数发生改变,当真空管道内压力从0.01 atm变化到1 atm时,真空管道内的单位雷诺数将会相差100倍,从而可能会对气动力产生影响。
图12为速度分别为600 km/h和1000 km/h时各车阻力系数随管道压力的变化图。从图中可以看出:当管道压力小于0.2 atm时,阻力系数随着管道压力的增加出现比较明显的下降,而当管道压力大于0.2 atm时,阻力系数随着管道压力的增加变化略微下降,变化很小。图13的升力系数随管道压力的变化图也表现出了相同的趋势,这说明了雷诺数变化大时,列车的气动力系数有较大不同。
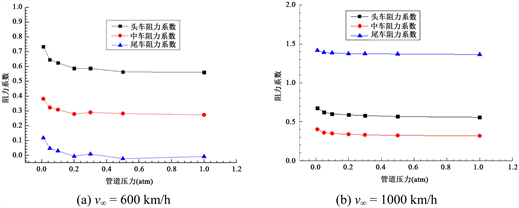
Figure 12. Coefficients of drag on tube pressure at different speed
图12. 不同速度下阻力系数随管道压力变化
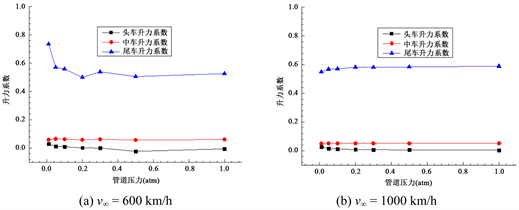
Figure 13. Coefficients of lift on tube pressure at different speed
图13. 不同速度下升力系数随管道压力变化
5. 结论
基于可压缩Naiver-Stokes方程,研究了低真空环境下管道面积、管道压力对磁浮列车气动特性的影响,得到了以下结论:
1) 低速运行时,低真空环境下磁浮列车与明线磁浮列车的流场特性相似。列车与管道组成的环状空间形成了拉瓦尔喷管效应,磁浮列车到达临界速度时,列车尾部会出现激波,管道面积不同时,管道中出现激波的磁浮列车临界速度不同。
2) 列车的气动力随着管道面积的减小而增大,列车尾部出现激波后,尾车的气动力会激剧增大。
3) 列车的气动力系数随着管道压力的增加下降,但管道压力变化大时,导致雷诺数变化大,从而列车的气动力系数有较大不同。
NOTES
*通讯作者。