摘要:
电缆卷绕是电缆生产的最终步骤,但实际中却缺少安全高效兼顾的检测方案,因而在卷绕时若电缆出现排列不整齐的情况,系统不能及时反馈。针对此问题,提出了一种基于半径约束的最小二乘圆拟合方法,用以实现电缆卷绕情况的测量。同时详细分析了各种因素对拟合精度的影响,并进行了仿真计算。
Abstract:
Cable winding is the final step of cable production, but in practice, there is no safe and efficient detection scheme. Therefore, if the cable is not neatly arranged during winding, the system cannot provide timely feedback. In order to solve this problem, a method of least square circle fitting based on radius constraint is proposed to realize the measurement of cable winding. At the same time, the influence of various factors on the fitting accuracy is analyzed in detail, and the simulation calculation is carried out.
1. 引言
在电缆的生产过程中,最后一道工序是将电缆紧密有序地卷绕在一定规格的卷筒上,电缆卷绕是否符合标准直接影响了电缆生产的合格率。若电缆间空隙较大,则电缆长度往往达不到相应卷筒的长度标准,在实际使用中,其长度不足也会对工程产生负面影响。
在电缆的卷绕过程中,电缆从卷筒一侧的内壁开始卷绕,随着卷筒的转动,电缆在水平方向上以一定的速度移动,到达卷筒另一侧的内壁时,确定返回点,随后电缆向相反方向移动,即在卷筒两侧的内壁间做水平往返运动,直至电缆全部盘卷完毕。理想情况如图1(a)所示,但在卷绕时,电缆往往存在排列不规整的情况。例如间隔过小,引起电缆相互挤压而凸起(图1(c)标号4);间隔过大,致使电缆排列不紧密(图1(b)标号3)等诸多情况。判断返回点时,每层两端的电缆距离卷盘内壁可能大于一根电缆直径(图1(b)标号1)或小于一根电缆直径(图1(c)标号2),返回点位置的确立也影响着电缆卷绕后两端的高度和层间落差,这些都会导致产品无法达到标准,影响产品的合格率。
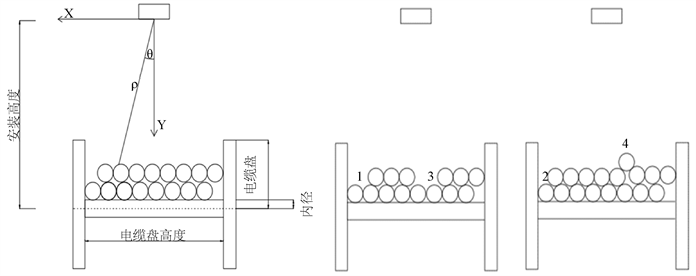 (a) (b) (c)
(a) (b) (c)
Figure 1. Alignment of cables. (a) In alignment; (b) Misaligned1; (c) Misaligned 2
图1. 电缆排列状态。(a) 排列整齐;(b) 排列不整齐1;(c) 排列不整齐2
2. 国内外研究现状
当前对于该问题的研究主要集中于电缆卷筒的控制方式上,而国内的电缆卷筒按照控制方式,已经发展到了第四代——变频式电缆卷筒,其可通过内部的计算机信息处理,使电缆在卷绕过程中其表面处于恒定的张力,有效避免了以往力矩恒定控制时,张力变化对电缆造成损伤。此外,它还可以提供“系统正常”、“系统运行”、“电缆满盘”三种反馈 [1] 。国外的研究人员研制了一种球形拖车式电缆卷筒机构,该机构由球形拖车和带振荡装置的电缆卷筒机构组成,可以使电缆均匀地缠绕在球形拖车上 [2] 。至于电缆卷绕监测方面,可见一种新型的移动卷缆检测系统,其可作为一种车载移动式检测设备。该设备组成有射线发射装置,用于向检测物品发射检测射线;探测器模块,与射线发射装置相对设置,用于接收来自射线装置发出的检测射线;图像处理装置,用于对探测器模块接收到的检测射线形成的检测图像进行处理 [3] 。但这套系统的成本较高,且该检测系统的安全系数还有待进一步提高。相比于射线对人体的伤害性和不稳定性,本文提出了一种以激光扫描为核心的更安全更高效的检测方案。
以激光传感器为切入点,也可以从当前的一些研究中获得启发。关于360˚激光测距的论文 [4] 中提到,采用移动平台搭载两路激光测距传感器,可以在水平和竖直方向同步进行距离和角度的数据采集,并将数据传输到上位机。上位机对所获得的距离数据进行融合,采用3D建模技术将离散的点拟合成移动平台周围环境的三维模型。在确定电缆排列状态的过程中,同样可以通过此种方法来判断电缆间距情况。
基于以上分析,使用两维激光扫描传感器,采集距离和角度数据,并设计数据分析算法,完成对电缆排列状态的监测。
3. 状态检测的算法设计
3.1. 基本原理
如图1(a)所示,传感器安装在电缆盘正上方。从正面看,由于卷绕中电缆形变较小,因而可将电缆的横截面视作圆形;由于电缆盘的形状为同轴圆柱体,因而可将电缆盘的侧边视作直线。所以,电缆的排列状态可做如下简化:① 电缆与电缆间的位置关系简化为圆与圆之间的位置关系;② 电缆与电缆盘侧边的位置关系简化为圆与直线之间的位置关系。
系统工作的基本原理为:激光传感器扫描电缆表面,并返回被测点的二维数据
,以传感器为原点,建立如图1中(a)的坐标系,并通过下式的坐标转换,将扫描点投影到直角坐标。然后对电缆盘边界与电缆圆心进行拟合,确定相互之间的位置关系,即可判断电缆的排列状态。
(1)
3.2. 算法设计
3.2.1. 数据预处理
静止状态下经过多次扫描,可得电缆与电缆盘同一截面的多组测量数据,将多初始数据求和取均值,可得一组预处理数据,对其拟合即可确定边界与电缆位置。
3.2.2. 确定边界位置
基于边界横坐标基本不变,从预处理数据中选取左右各N个点的横坐标求取算数平均值,作为边界位置的估计值
、
。
(2)
其中N越大,边界位置的估计值误差越小。然后将剩余预处理数据中满足
的坐标筛选出来,作为电缆位置拟合的输入数据。
3.2.3. 确定电缆位置
目前检测圆的常用算法有Hough变换圆检测 [5] [6] 、最小二乘圆检测 [7] [8] 、几何特征圆检测 [9] 等。但Hough变换圆检测计算量大,拟合时间长;几何特征圆检测虽计算量少,但易受单个点影响,误差较大;所以针对本文的问题,考虑到传感器输出数据的顺序性和电缆规格的已知性,可采用半径约束的最小二乘法 [10] 来确定圆的位置,即将电缆的理论半径作为约束条件来进行最小二乘圆的拟合,其原理如下:
圆方程的一般形式可表示为:
(3)
因而可以构造如下目标优化函数:
(4)
式中:
为圆弧上的扫描点,
为使
最小时的最优解,也即拟合的圆心与半径,N为参与拟合的特征点个数。若拟合出的圆半径
小于误差允许范围,即可认定为目标圆之一。
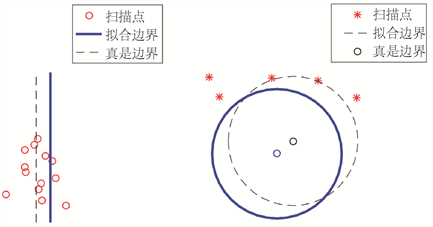
其中,边界与电缆的拟合过程如图2。
 (a) (b)
(a) (b)
Figure 2. The fitting process. (a) The process of fitting a line; (b) The process of fitting a circle
图2. 拟合过程。(a) 直线拟合过程;(b) 圆拟合过程
在检测单个圆的基础上,可以设计出如图3的多圆检测算法。确定边界与电缆位置后,即可判断其相互间的位置关系。
4. 拟合精度影响因素及扫描次数确定
受传感器精度、电缆及电缆盘反光率、获取圆弧长度、室温等多种因素的制约,提取电缆及电缆盘边界上的特征点数据必然存在噪声,此外拟合算法对拟合精度也有影响,因而为达到检测的精度要求,需多次测量,利用扫描点的均值进行拟合。
基于本文采用的拟合算法,暂不考虑环境因素的制约,且扫描过程中每根电缆获取的圆弧长度基本不变,因而影响拟合精度的主要因素有数据量、数据精度、约束半径。其中数据量取决于参与拟合的特征点数目;数据精度取决于传感器的测量误差及其角分辨率;约束半径为先验知识,可以作为输入量。下面,用仿真的方法来逐一分析当数据量、数据精度、约束半径这三种因素变化,且满足边界的拟合误差小于1 mm,电缆圆心的拟合误差小于1%电缆直径时,所需要测量的平均次数。
4.1. 模型建立
取电缆盘宽度D = 1120 mm,电缆盘内外径差H = 800 mm,传感器安装在电缆盘正上方居中,且安装高度h = 2000 mm。又因电缆所处位置不影响数据量、数据精度、约束半径这三种因素,因而以单根电缆来分析圆拟合误差,并设电缆位置的圆方程为
,其中r/mm为电缆半径。
另据表1的传感器参数,取传感器的角度误差的标准差
,固定不变,长度误差的标准差
,随外界条件改变,以此作为一倍噪声;取传感器的角度分辨率
,随设置改变,以此作为一倍角分辨率。

Table 1. Parameters of sensor LMS400
表1. LMS4000传感器相关参数
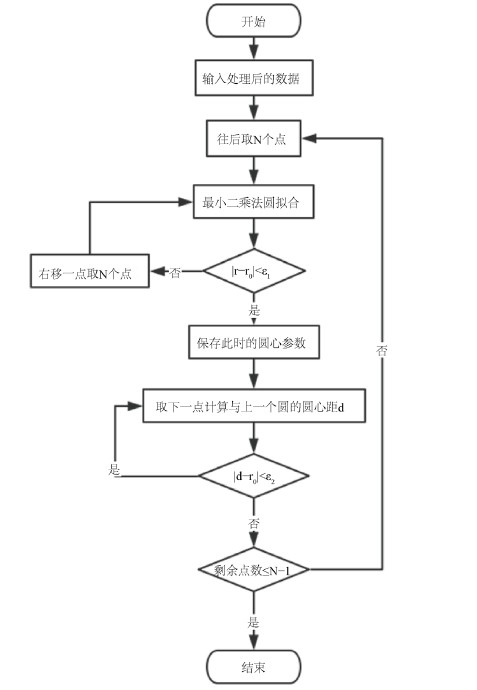
Figure 3. Flow chart for determining the center of circles
图3. 多圆圆心判断流程图
4.2. 边界拟合
影响边界拟合精度的因素有数据量和数据精度。
设特征点个数为2时为一倍特征点,边界拟合时所需平均扫描次数为T1。取一倍噪声,一倍角分辨率,改变特征点倍数,比较T1变化;取3倍特征点(特征点个数为6),一倍角分辨率,改变噪声倍数,比较T1变化;结果如图4。
图4表明:平均扫描次数T1随特征点倍数增加而减小,随噪声倍数增加而增加,但平均扫描4次以内,即可使边界的拟合误差小于1 mm。
4.3. 电缆圆心拟合
考虑到充分利用电缆上的扫描点,即将电缆上的扫描点都作为特征点参与拟合,所以不考虑数据量对电缆圆心拟合精度的影响,即影响电缆圆心拟合精度的因素有数据精度和约束半径。
设电缆半径为10 mm时为一倍约束半径,电缆圆心拟合时所需平均扫描次数为T2,以拟合圆心到实际圆心距离为拟合偏差。取一倍噪声,3倍约束半径(r = 30 mm),改变角分辨率倍数,比较T2的变化;取一倍角分辨率,一倍约束半径,改变噪声倍数,比较T2的变化;取一倍噪声,一倍角分辨率,改变约束半径倍数,比较T2的变化。结果如图5。
5. 相关要求
基于上述算法,以及表1和图6中的传感器参数,需要对电缆规格、电缆盘规格、卷绕速度、安装位置提出一定的要求。
5.1. 电缆规格
基于本文采用的算法,对一个圆的拟合至少需要3个特征点。因而需确保在扫描过程中,每根电缆上至少有3个扫描点。电缆的极限扫描情况如图7,此时电缆上恰好有3个扫描点,且距离传感器最远。另取如表1所示的电缆盘规格,则当传感器的参数分别取
时,电缆的半径r应满足:
(5)
求解得,电缆的半径r应大于7.3 mm。且结合4.3中仿真分析,此时平均需要140次扫描,可使电缆圆心的拟合误差小于1%电缆直径。也可在实际应用中,可根据检测精度要求,减少扫描次数,提高响应速度。
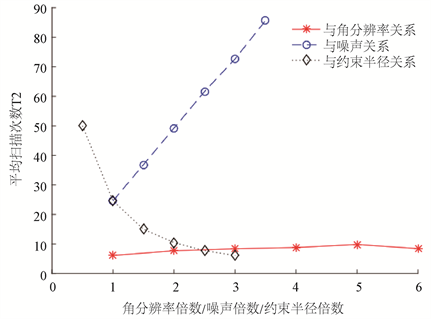
Figure 5. Fitting error of cable center
图5. 电缆圆心拟合误差
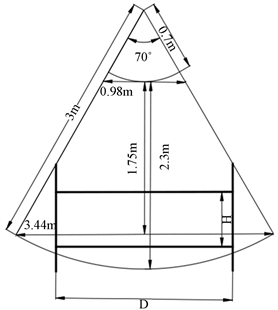
Figure 6. Schematic diagram of sensor detection range
图6. 传感器检测范围示意图
5.2. 卷绕速度
在电缆卷绕过程中,其排列状态会随电缆盘的旋绕而改变,所以为保证电缆排列状态能及时反馈,电缆盘旋绕一圈的时间t应大于检测精度要求的扫描时间T。
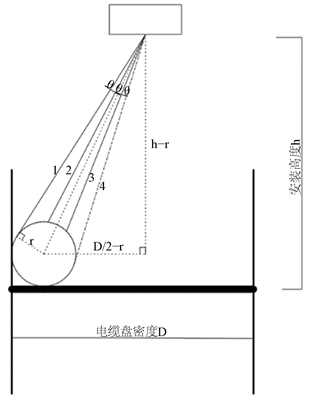
Figure 7. Determination of cable specifications
图7. 电缆规格确定
设满足检测精度要求的平均扫描次数为T2,传感器的扫描频率为f/Hz,则电缆盘选装一圈的时间t应满足:
(6)
5.3. 电缆盘规格
LMS400的检测范围如图6所示,考虑传感器的扫描范围充分覆盖电缆盘及电缆,所以适当缩小有效检测范围以确保检测的准确性。以角度范围60˚,长度范围0.8 m至2.9 m为例进行计算,实际应用中可对检测范围的取值做相应调整。
设电缆卷筒内宽为D(m),电缆卷绕完成后高度为H(m),则电缆盘的规格要求如下:
(7)
(8)
5.4. 安装要求
在实际的操作中,传感器很难恰好安装于电缆盘上方的中央位置,但只要电缆处于传感器的检测范围内便不影响监测,在不同的情况下传感器可以偏离电缆盘中央位置的程度也不同。
设电缆卷盘内宽为D,电缆卷绕完成后高度为H,传感器距离电缆卷盘所在水平线的垂直距离为h,在检测范围内对于不同的h,D可取的最大值为f(h),传感器在检测范围内的最大偏移量为g(h)
1) 电缆卷盘内宽最大值
(9)
2) 当
时
(10)
(11)
3) 当
,
时
(12)
(13)
4) 当
,
时
(14)
(15)
(16)
影响传感器最大偏移量的参数为h,H,D,需要在检测范围内,结合具体参数以及实际的安装位置进行综合考量。
6. 总结
以上是电缆盘卷过程中对电缆排列情况的监测分析,在目前研究的基础上提出了采用两维激光扫描传感器检测的方式,能更快更准确地发现电缆卷绕时出现的问题,基于本算法,由公式(5)得出LMS400激光扫描传感器可监测直径大于等于14.6 mm的电缆卷绕情况。整套装置结构简单,安装方便,为电缆卷绕的状态测量提供了一种全新的选择。但该算法仍有需要改进之处,对于目前的仿真缺少实验验证;在应用于实际系统时,电缆表面由何种材料构成也是需要考虑的因素,不同的材料会影响传感器的测量精度,数据误差将会更加复杂。同时,传感器的数据测量传输和算法的计算分析是一个动态适配的过程,不同情况下的监测对应着不同的计算参数。后续还需要优化算法对误差的处理来提高实际情况下拟合的精确性,并提高算法的简洁度和通用性。
基金项目
本论文受到国家级大学生创新创业训练计划项目经费资助,项目编号:201810288045。