浅谈线性代数课程的教学

A Brief Talk on Linear Algebra Teaching

摘要: 本文主要以高等教育院校开设的公共课线性代数为例。通过分析线性代数的结构体系，以线性方程组理论为主线，讨论线性代数实际教学过程中的教学思路。

Abstract: In this paper, we mainly study linear algebra as a common course in higher education institutions. By analyzing the structural system of linear algebra and focusing on the theory of system of linear equations, we discuss the teaching idea in the actual process of teaching linear algebra cause.

1. 引言

目前《线性代数》是我国高等院校理工科和经管类专业开设的一门非常重要的数学基础课程之一。《工程数学线性代数》 [1] 主要包括行列式、矩阵、线性方程组、向量、二次型、线性空间与线性变换等内容。事实上，线性代数主要研究问题可归结为线性方程组的求解及其相关问题。线性方程组的理论与方法几乎贯穿在线性代数教材的各章之中。通过线性方程组的不同表现形式可引入行列式、矩阵、向量等概念，通过线性方程组的求解也可将各章节相关内容联系在一起，从而使这门课程各部分内容融为一体。

2. 线性代数的主线——线性方程组

对学生而言，线性代数跟以往学过的数学知识完全不同，学生普遍认为这门课程内容过于抽象、定理定义太多、解题方法较为复杂，无法将课程前后各章节内容联系在一起。因此，在正式讲授课程内容之前，教师应努力讲清楚各部分知识的联系，将各部分内容合理地衔接起来，理清课程脉络，注意前后内容的衔接 [2] 。所以，以求解线性方程组作为主线是比较合理的。一方面，线性方程组是学生比较熟悉的概念，以线性方程组为课程的主线学生更易于接受；同时以线性方程组为主线也能够很好地将各部分内容串联起来。从学生中学最为熟悉的线性方程组出发，将线性方程组分为方程个数和未知量个数相等或不等两种类型 [3] 。由简入难，以二元和三元方程组引出二阶和三阶行列式的定义，从而引出一般行列式的定义，继而得到克拉默法则；而“对于方程个数和未知量个数不同的线性方程组的求解问题”则需引入矩阵的概念及其相关定义、性质与矩阵的秩等重要概念，然后借助矩阵的秩可以观察线性方程组中哪些是有解，哪些是无解的，接着引出向量由向量组线性表示问题，进一步引出线性相关(无关)的概念；同样，由观察齐次线性方程组的解的集合所具有的性质可引出而线性空间这个核心概念；最后，化二次型为标准型便是将前面知识进行了综合应用，其中的内容涉及到矩阵的对角化，特别是求解矩阵特征向量又涉及到线性方程组的求解。因此，将线性方程组作为主线来串联线性代数各部分内容十分有助于学生从整体上去理解线性代数这门课程。

对于线性方程组的求解，中学数学中只涉及到未知数个数n与方程个数m相同，并且n或m较小的线性方程组，通常采用消元法进行求解。而大学中线性代数这门课程将会介绍更为高级、简便的方法来求解任意线性方程组。设有n个未知数与m个方程的线性方程组，一般表示为：

$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1,\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2,\\ ⋮\\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=b_m.\end{array}$

由此，可将线性方程组分为两大类：

1) $m=n$，即方程个数与未知数个数相等。

2) $m\ne n$，即方程个数与未知数个数不相等。

求解以上两类线性方程组需要用到两类有力工具，那就是行列式和矩阵。由此，可将线性代数的课堂教学内容重点分为三大部分。

3. 课堂教学重点内容1：行列式

鉴于之前据方程个数和未知量个数不等或相等将线性方程组分为两类。在教学安排上首先介绍行列式，并告知学生行列式的出现是为了求解第一类线性方程组—— $m=n$。从学生最为熟悉的二元线性方程组引入二阶行列式，使学生对行列式有初步了解。接着由三元线性方程组引出三阶行列式，进而推广到n阶行列式的一般定义。接下来便是针对n阶行列式内容的讲授。事实上，行列式骨子里就是一个代数表达式。因此计算行列式的代数表达式是学习行列式首要任务。那么便需掌握计算行列式的常用方法，也是行列式内容的重点：n阶行列式的定义法、行列式性质、降阶法、升阶法(加边法)、数学归纳法、递推法。万事俱备，最后便可采用行列式得到克拉默法则，从而求解方程个数等于未知数个数且系数行列式不等于零的线性方程组。最后，结合二阶行列式与二元线性方程组的关系，可推广到n元线性方程组的求解——克拉默法则：

克拉默法则 [1] ：如果线性方程组 $\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=b_2\\ ⋮\\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n=b_n\end{array}$ 的系数行列式不等于零，即 $D=\left|\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right|\ne 0$，那么方程组有唯一解：

$x_1=\frac{D_1}{D},x_2=\frac{D_2}{D},x_3=\frac{D_2}{D},\cdots ,x_n=\frac{D_n}{D}$

其中 $D_j\left(j=1,2,\cdots ,n\right)$ 是把系数行列式D中第j列的元素用方程组右端的常数项代替后所得到的n阶行列式，即 $D_j=\left|\begin{array}{ccccccc}{a}_{11}& \cdots & a_{1,j-1}& b_1& a_{1,j+1}& \cdots & a_{1n}\\ ⋮& & ⋮& ⋮& ⋮& & ⋮\\ a_{n1}& \cdots & a_{n,j-1}& b_n& a_{n,j+1}& \cdots & a_{n,n}\end{array}\right|$。

到此，克拉默法则回答了最初关于求解 $m=n$ 的线性方程组的问题。教学过程中，让学生去观察以上条件，并提出问题：克拉默法则不能求解两大类线性方程组的哪些方程？显然，对于 $m\ne n$ 或系数行列式为0的 $m=n$ 的线性方程组，克拉默法则已失效。由此，需要引入另一工具——矩阵。

4. 课堂教学重点内容2——矩阵

矩阵是克拉默法则求解某些线性方程组失效后的产物，更是数学家偷懒的结果。学生在中学阶段求解线性方程所采用的消元法是一个重复与繁琐的过程，在此过程中会发现参与运算过程的仅仅是未知变量的系数，那么将这些系数按照在方程组中的位置依次排列，再用括号括起来，便得到与原方程组相应的一个数表，称之为矩阵。所以，矩阵本质上是一个长方形数表，其作为求解线性方程组的另一有力工具，与线性代数中其他内容都有着千丝万缕的联系。利用矩阵求解线性方程组取代了中学时代需要将每次消元后的方程组重新抄一遍的繁琐，达到事半功倍的效果。事实上，矩阵适用于求解所有线性方程组，大多时候比克拉默法则更为简单，方便。因此，矩阵作为一种新的工具，我们需要认识和理解它。如，矩阵的四则运算，矩阵的性质。通过与数的运算进行对比，记住矩阵加减、乘以及逆运算的条件，并注意矩阵的一些反常性质，如矩阵的乘法不在满足交换律与消去律，全不为零矩阵相乘可能为零。

在介绍完矩阵的基本运算与性质后，学生还需掌握矩阵的秩。矩阵的秩是矩阵的核心，是矩阵的一个重要的数值特征，是矩阵判断解线性方程组是否有解及求解的过程中的必经之路。矩阵秩的概念较难理解，它的影响力却不容小觑。矩阵的秩的应用贯穿了几乎整本教材。例如，判断线性方程组是否有解、判断向量组的线性相关性、求矩阵特征值、判断二次型的正定性等等方面都与矩阵的秩息息相关。因此，结合增广矩阵秩的性质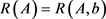：或 $R\left(A\right)+1=R\left(A,b\right)$，便得到线性方程组 $A_{m\times n}x=b$ 的求解理论：

定理 [1] ：给定n元线性方程组 $A_{m\times n}x=b$，则方程

1) 无解的充分必要条件是 $R\left(A\right)\ne R\left(A,b\right)$；

2) 有解的充分必要条件是 $R\left(A\right)=R\left(A,b\right)=r$。

a) 有唯一解 $\iff r=n$；

b) 有无限多解 $\iff r<n$。

因此，求任意方程组 $A_{m\times n}x=b$ 的解都可以通过对增广矩阵 $B=\left(A,b\right)$ 讨论得以解决。

5. 课堂教学重点内容3——线性方程组及矩阵的应用

5.1. 向量组的线性相关性

教师在介绍线性相关性之前，需要向学生介绍线性方程组常用的四种表示形式，例如：

1) 一般表达式： $\{\begin{array}{l}{x}_1+x_2=2\\ 2x_1+3x_2=5\end{array}$；

2) 增广矩阵形式： $\left(\begin{array}{ccc}1& 1& 2\\ 2& 3& 5\end{array}\right)$ (矩阵求解线性方程组的重要工具，但需要附加说明)；

3) 矩阵相乘形式： $\left(\begin{array}{cc}1& 1\\ 2& 3\end{array}\right)x=\left(\begin{array}{c}2\\ 5\end{array}\right)$，即 $Ax=b$ (无需说明)；

4) 向量线性组合形式： $\left(\begin{array}{c}1\\ 2\end{array}\right)x_1+\left(\begin{array}{c}1\\ 3\end{array}\right)x_2=\left(\begin{array}{c}2\\ 5\end{array}\right)$。

以上四种不同的表示形式，在线性代数中却有着不同的意义。而表达形式4)恰好与线性代数中另外一个重要概念——线性表示有着重要联系。这样，学生更容易理解线性表示的定义。因此，判断向量 $b$ 是否可以由向量组 $A$ 线性表示？若可以表示，求出表达式的问题自然就转化为判断线性方程组 $Ax=b$ 是否有解，并求解的问题。在此基础上，若令 $b=0$，由线性表示便可得到向量组 $$ 线性相关性的概念。向量组的线性相关性是线性代数中非常重要概念之一，也是线性代数中的难点。给定向量组 $A$，不是线性相关的，就是线性无关的，两者必居其一。通过前面分析，判断向量组 $A$ 的线性相关性本质上是判断齐次线性方程组 $Ax=0$ 是否有非零解的问题。再通过线性相关性可讲授最大无关组的概念，便可发现通过有限向量组掌握无限向量组，凡是对有限向量组成立的结论，用最大无关组作过渡，立即可推广到无限向量组的情形中去。在线性相关性的教学过程中，教师需要强调判断向量组线性相关性的重要性，并说明通常采用以下四个等价命题：

向量组 $A$ ： ${\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m$ 线性相关：

$\iff$ 存在不全为零的实数 $k_1,k_2,\cdots ,k_m$，使得 $k_1{\alpha }_1+k_2{\alpha }_2+\cdots +k_m{\alpha }_m=0$。

$\iff$ m元齐次线性方程组 $Ax=0$ 有非零解。

$\iff$ 矩阵 $A=\left({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_m\right)$ 的秩小于向量的个数m。

$\iff$ 向量组 $A$ 中至少有一个向量能由其余m个向量线性表示。

同理，很容易得到判断线性无关的四个等价命题。

5.2. 相似矩阵及二次型

相似矩阵及二次型主要是对实对称矩阵的研究。化二次型为标准型便是将前面知识进行了大串联。由于二次型与对称矩阵有密切的联系，而讨论对称矩阵又会涉及到矩阵的秩、矩阵的初等变换、矩阵的特征值特征向量等概念，求解矩阵特征向量又会用到线性方程组的求解。通过求解线线方程组可将实对称矩阵对角化。可见，这部分内容中求解线性方程组仍起着举足轻重的作用。因此，这部分内容是对前面章节知识的巩固与融合。

基金项目

海南大学教育教学研究课题立项项目“大学数学MOOC与翻转课堂相结合的教学研究” (编号：hdjy1819)、大学数学教与学的趣味性探究(hdjy1853)；海南省高等学校教育教学改革研究资助项目“大学数学MOOC与翻转课堂相结合的教学研究” (编号：Hnjg2018-4)。