1. 引言
多相流一直是困扰研究人员和工业过程的难题。非均匀速度,时空不稳定性和混合相的不同复杂特性是多相流的主要特征。在流体检测中可能导致流动不稳定、混合不均匀、时间和空间不稳定的相界,复杂的流动模式以及一相吸收到另一相的问题 [1]。
以前,相分离和手动测试用于多相流测量。在分离法中,气液两相流体通过分离设备分离成单相流体,然后用单相流量计测量。虽然简单、可靠且对流型变化不敏感,但系统的尺寸,成本和非自动化是其最大的缺点。并且由于采样和手动测试方法不准,难以反映原分相流量。此外,人们在测量多相流方面做了大量工作,并且已经使用了许多方法。然而,除了快关阀之外,几乎没有通用的方法,快速截止阀技术不能用于实际生产过程中的分相含率检测,因为它需要切断正常的流动采样 [2]。这需要在理论和测量方面进行转换,以解决两相流中分相含率的持续测量问题。
过程层析成像(PT)——发明于20世纪80年代,侧重于将多相流作为主要目标,作为过程参数在二维和三维分布中的检测技术。在中国,天津大学和清华大学是最先开始研究,后来浙江大学,东北大学和浙江工业大学开发了几种PT技术原型系统 [3] [4] [5]。在全球范围内,英国曼彻斯特理工大学和英国利兹大学,美国摩根敦能源技术中心,挪威卑尔根大学为PT的研究做出了贡献,包括电磁,电,磁,超声等断层成像方法 [6]。
计算机断层扫描和光学层析成像技术是两种电磁辐射方法。基于光和物体之间的不同接触模式存在不同的光学层析成像技术,包括吸收模式,衍射模式,反射/折射模式,辐射和干涉模式等 [7]。例如,Uchiyama [8] 和Hertz [9] 分别使用红外辐射和干涉来研究火焰温度分布。电磁辐射具有非侵入性,响应速度快,分辨率高,介质中光传播可定量描述,抗干扰能力强,光能低时安全性好等优点 [10]。然而,它的缺点是存在吸收,散射,多次反射和折射,如像工业管道等一些不透明的测量介质和像核反应堆等一些复杂的机械结构,且由于辐射特性,它对人类有一定危害。
电学层析成像(ET)系统广泛用于工业和医学检测。它的优点是:非侵入性,甚至非接触式,成本低,结构简单,无辐射;它可以在更高的激发频率(兆赫级别)下运行,以实现更快的图像采集速率。基于物理学理论:不同的介质具有不同的电学性质 [11]。ET技术根据其测量的电气特性分为电阻抗层析成像(EIT)和电荷层析成像。
电阻抗层析成像(EIT),基于物体的电导率和介电常数的测量,然后重构物体电阻或电抗的分布 [12],可分为电阻层析成像(ERT)和电容层析成像(ECT) [13] [14]。ERT和ECT的缺点是对三维模型的研究较少,电极板数量有限,重构算法有待优化,抗干扰和实时性能有待提高,工业化困难。电荷层析成像通过测量与管道摩擦产生的带电粒子的横截面分布来获得两相介质中的固相分布。该方法响应速度快,安全性好,成本低,但由于影响因素很多,仅适用于被测液体带电的场合 [2]。
磁共振成像(MRI)是一种诊断技术,它利用人体组织中的核磁共振(NMR)现象通过计算机处理射频信号并重构一定部位的人体图像,它也称为核磁共振成像。MRI属于非侵入性,非射击线检查,避免了X射线或放射性核素对成像的影响,对人体无害。MRI成像的参数很多,包括大量信息,空间分辨率高,但一般的核磁共振设备比较昂贵,在一定程度上限制了它的推广应用 [15]。
超声计算机层析成像(UCT)根据多相流内的介质的声学反射特性来检测介质的位置和大小。其原理是被测介质通过反射,透射,衍射和多普勒效应影响声波的传播,通过接收器检测被测介质的变化,并通过一些图像重构来计算被测介质的分布。UCT的优点是应用范围广,成本低,安全性高,缺点是传播速度慢,实时性差,不适用于多相流不同相位之间声阻抗差异较大的情况,影像效果不理想 [2]。
基于上述过程的层析成像方法,本文提供了一种新颖的方法,选择可以避免局部机械结构的二维横截面——检测区域,通过少量传感器测量检测区域中相应的过程参数,并且结合CFD数据库利用数学方法可以重构整个检测区域的过程参数分布,可用于流体检测等。这种方法最大的优点在于不再需要计算复杂的敏感场,且可以更快速,更准确地测量流场 [16]。
2. 数学模型
2.1. 重构方法数学描述
通过少量传感器(也称为采样点)导出整个流场的过程参数的基本数学模型可以用以下公式表示:
(1)
——实际过程参数矩阵(如:流速,体积分数等),维度为
;
——已知变换矩阵,维度为
;
——测量所得的过程参数矩阵,维度为
。
过程参数矩阵Y代表不同条件下的原始流场,其可通过流场CFD模拟(使用
湍流模型)确定。矩阵A表示事先已知的变换矩阵(测量术语中的测量矩阵)。重构算法的目标是通过最少的V确定Y (因此需要测量最小数量的过程参数)。公式(1)是一个逆解问题,需要通过减小Y的维数来解决。重构的过程参数矩阵
可以用下列公式表达为降维形式:
(2)

(3)
——重构过程参数矩阵,维度为
;
——基矩阵,维度为
;
——重构系数矩阵,维度为
(
);
——第
节点基矩阵线性组合系数。
在感兴趣的区域获得样本矩阵Z (代表真实过程参数),并进行如下分解:
(4)
——流场过程参数样本矩阵(包含n种不同工况),维度为
;
——基矩阵,维度为
;
——分解权重矩阵,维度为
;
——分解误差矩阵,维度为
。
将
表示为低秩矩阵
和
的乘积加上
,这种数学变换有助于减小问题的维数并获得主要的信息。
将重构过程参数矩阵
带入方程(1),可表示为:
(5)
由于存在分解误差,则Y和
是不相等的,得到公式(5)之后就可求解
,进而由公式(2)获得
。
可以通过最小二乘法拟合最小化函数f来求解:
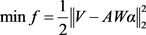 (6)
(6)
重构相对误差
可以通过实际过程参数矩阵Y和重构过程参数矩阵
求得:
(7)
为了实现整个重构过程,在MATLAB中编写了基于非负矩阵分解的MATLAB重构算法(Matlab algorithm based on NMF for reconstructing, MNR),如图1是整个算法流程图。
2.2. 非负矩阵分解(NMF)
非负矩阵分解是由Lee和Seung于1999年在Nature于1999年发表 [17],并且在2001年提出了非负矩阵分解算法 [18],具体过程如下:
(8)
(9)
where
,
;
对任意两个具有相同维度的矩阵B和C,定义如下两种的损失函数:
平方距离法:
(10)
Kullback-Leibler散度法:
,(当且仅当
;
) (12)
对应不同的损失函数
,需要求解以下最小化问题,从而得到最佳的分解结果:
(11)
(12)
文章利用MATLAB已有的非负矩阵算法对流场过程参数样本矩阵Z进行分解,获得基矩阵W。
3. CFD模型
为了验证该方法是否可靠,即利用CFD获得的重构基矩阵能否很好地重构流场,或者重构的流场能否真实地反映原CFD流场,需要进行两者之间的比较。对于这个比较,测量所得的过程参数矩阵(V,在方程(1)和(5)中)取值于CFD样本数据库。因此,首先要建立流场CFD模型。
几何模型如图2(a)所示,冷却水从下部A进入,并在向上流动期间从加热棒吸收热量,然后从B流出。如果发生加热棒泄漏,例如在D和G点,则泄漏材料C和 F将由流体携带到冷却水的顶部E和H区域,最终从B排出。
在CFD模拟中,为了简化几何模型,选择图2(a)中红色虚线之间的区域作为构建几何模型的参考,图2(c)和图2(d)列出了模型尺寸。距离冷却水出口(M-M) 0.2 m的平面是检测区域,即传感器布置区域。该模型包含25个均有可能发生泄露的加热棒,并在图2(b)中对其命名。为了比较不同加热棒和泄漏速度对泄漏物质分布的影响,采用可变控制方法将所有泄漏排列在同一高度,保持泄漏方向一致。在ANASYS16.0 ICEM中,建立了如图2(e)所示的模型。
根据压水堆计算出相应的边界条件,冷却水入口设置为速度入口,流速为0.2 m/s,出口设置为压力出口,压力为15.5 MPa;加热棒温度为650 k;而泄漏物质设置为速度入口,速度分为两个阶段,第一阶段为0.01 m/s、0.02 m/s、……、0.06 m/s,第二阶段为0.1 m/s、0.15 m/s、……、0.6 m/s,目的是为了更全面的反应泄露情况并且得到一个更加详实的样本数据库。
该模型由ANASYS16.0 FLUENT求解。网格独立性检查已完成,模型的总网格节点数为379670。工作冷却介质为水,泄漏材料为甲烷。三维定常不可压缩模型以及雷诺时均N-S方程用于描述计算域中的内部流场。选择SIMPLE算法作为压力和速度的耦合方法。分析类型为“稳态”,计算残差收敛标准设置为1e−5。采用标准湍流模型,一阶迎风差分格式,选择标准壁面函数的默认值和模型常数。工作压力为15.5 MPa,冷却剂入口温度为560 K。梯度设置为“最小二乘单元格”,迭代步数为1500。
4. 重构结果
样本数据库
来自于检测域,当每根加热棒以不同的泄露速度泄漏时,在检测域上就可以得到一个实际过程参数矩阵
,现共有两阶段不同泄露速度17种,不同加热棒25根,可得到共425个实际过程参数矩阵
组成样本数据库
,即n = 425;为了反映实际的流场和给采样提供样本点,在检测域上划分样本点,由于检测域是圆形,为了采样更充分,采用类似极坐标的方法划分检测域,采样结果形成测量所得的过程参数矩阵
,x代表采样数量,也是传感器数量;同时为了对照,共有两种样本点数量不同的两种结果,一种是沿半径方向100等分,沿圆周方向180等分,共17821个样本点;另一种是沿半径方向50等分,沿圆周方向90等分,共4411个样本点。形成两个样本数据库
,一个为
,另一个为
。
重构时需要先采样,采样点数量(
中的x)分为100、150、……、700、750共14组,每组包含10种随机生成的相应数量的采样点,即相同采样点数量,但不同位置,表示为位置1、位置2、……、位置10。分别选择体积分数和速度这两个流场中的过程参数进行重构,重构结果如下。
4.1. 体积分数重构结果
下文由图片进行比较的重构结果和实际结果所选取的采样点数为500,样本点数为17821,采样率为2.8%,采样位置为位置1,重构基矩阵
包含75个基矢量(k = 75)。同时,先对包含在样本数据库中的泄漏速度(例如0.6 m/s)所形成的流场的重构结果进行比较,再对未包含在样本数据库中的泄露速度(例如0.7 m/s)所形成的流场的重构结果进行比较。
当泄漏速度为0.6 m/s时,泄漏物质的质量流量为0.0112 kg/s,相对重构误差为4.11%。如图3(a)和图3(b)所示,可以确认泄露位置为第一根加热棒;并由图4(a)和图4(b)可知,二者轮廓是基本一致的,重现了泄漏物质分布,重构结果是匹配的。
 (a) (b)
(a) (b)
Figure 3. Volume fraction reconstruction result when the leakage velocity of 1 is 0.6 m/s. (a) Actual result; (b) Reconstruction result
图3. 泄露速度为0.6 m/s时的体积分数重构结果。(a) 实际结果;(b) 重构结果
 (a) (b)
(a) (b)
Figure 4. Partial enlargement of the volume fraction reconstruction result when the leakagevelocity is 0.6 m/s. (a) Actual result; (b) Reconstruction result
图4. 泄露速度为0.6 m/s时的体积分数重构结果局部放大图。(a) 实际结果;(b) 重构结果
 (a) 实际结果 (Actual result) (b) 重构结果 Reconstruction result
(a) 实际结果 (Actual result) (b) 重构结果 Reconstruction result
Figure 5. Volume fraction reconstruction results when the leakage velocity of 1 is 0.7 m/s
图5. 泄露速度为0.7 m/s时的体积分数重构结果
 (a) 实际结果 (Actual result) (b) 重构结果 Reconstruction result
(a) 实际结果 (Actual result) (b) 重构结果 Reconstruction result
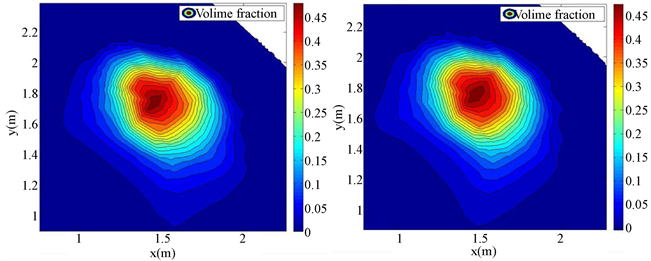
Figure 6. Partial enlargement of the volume fraction reconstruction result when the leakagevelocity is 0.7 m/s
图6. 泄露速度为0.7 m/s时的体积分数重构结果局部放大图
当泄漏速度为0.7 m/s时,泄露所形成的工况本身不包含在样本数据库中,结果如图5(a)和图5(b)相对重构误差为4.5%。如图6(a)和图6(b)所示,二者轮廓也是基本一致的,实现了利用有限的样本数据库提取基矩阵来实现任意工况下的流场重构,这也是可以利用CFD模拟流场结合少量传感器就可以实现实际流场重构的原因,前提条件是CFD模型要尽可能的还原实际流场,使得重构误差满足工程实际要求;同样,也可在满足工程误差要求的情况下,尽量简化CFD模型。
4.2. 速度重构结果
多次尝试不同的泄露速度并在其他条件与上述条件保持一致的情况下对速度场进行重构,对比多个不同的重构结果可知泄露速度对整个流场流速基本没有影响,流场模式主要取决于冷却水入口流速,结果如图7(a)和图7(b)所示,相对重构误差约为0.17%。由此可见,本文所述的重构方法对于没有较大数量级差异的过程参数的重构效果更佳,由于体积分数存在很大的数量级差异,所以重构效果并没有速度场重构效果好。
 (a) 实际结果 (Actual result) (b) 重构结果 Reconstruction result
(a) 实际结果 (Actual result) (b) 重构结果 Reconstruction result
Figure 7. Reconstruction result of velocity
图7. 流速重构结果
5. 讨论
对于不存在数量级差异的过程参数的重构,如本文的速度,由于冷却水入口流速为均匀流速而造成的检测域上速度场没有大的数量级差异,所以重构误差一直较小,在0.2%左右波动;对于存在较大数量级差异的过程参数的重构,如本文的体积分数,误差将受不同因素的影响发生较大的变化,下面将从基矩阵、采样点、泄露等不同因素分析对体积分数重构结果的影响。
5.1. 基矩阵
在分析基向量数的影响时,选择的泄漏位置为加热棒1,泄漏速度为0.6 m/s,采样点数为500,采样位置为位置1。对样本数据库分解10次获得10个包含相等基向量数量的基矩阵,将这10个基矩阵代入MNR算法,并对10组相对重构误差求平均,得到相应的y坐标值。分别对样本维度为17821和4411的样本进行了计算,结果如图8所示,随着基向量个数增加,相对重构误差先减小后基本保持不变,这符合非负矩阵分解提取样本数据库特征的特点,基矩阵中的前40个基向量基本占据整个样本数据库的能量,所以当再增加基向量个数时,相对重构误差基本保持不变。同时,由于非负矩阵分解结果的随机性同一基向量数量的基矩阵重构效果不同,尤其当采样率相对较低时,基矩阵的优劣对重构结果有较大的的影响,如图中样本维度为17821样本时,基向量数量从20到40,误差出现了波动,但对样本维度为4411的样本则不会情况出现。所以,在选取基矩阵时,在条件允许的情况下尽可能地进行多次分解寻找一个较优的基矩阵。
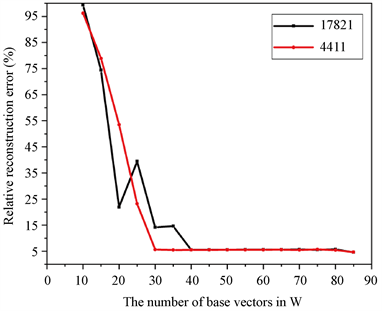
Figure 8. Reconstruction result of different basis matrices
图8. 不同基矩阵的相对重构误差
5.2. 采样率
在分析采样率的影响时选择的泄漏位置为加热棒1,泄漏速度为0.6 m/s,最佳基向量数为75,采样点数从100个到750个。同样数目的采样点进行10次随机采样得的10组相对重构误差,其平均值为y坐标值。分别对样本维度为17821和4411的样本进行了计算,结果如图9所示,随着采样率的上升误差先减小然后保持基本不变,这是比较显而易见。而重要的是无论样本维度为4411还是17821,采样点都应至少为150个,由此可见对于样本维度越大的样本,重构算法的降维效果越明显,完成重构所需的采样率越小,能够实现利用少量的传感器重构流场这一目的。
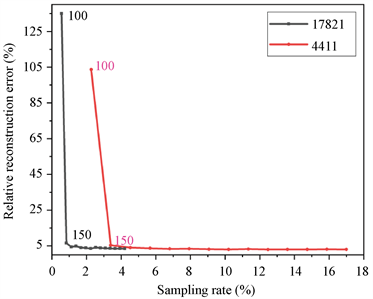
Figure 9. Relative reconstruction error corresponding to different sampling rates
图9. 不同采样率对应的相对重构误差
5.3. 泄露
在分析泄露的影响时,最佳基向量数为75,采样点数为500个,同样数目的采样点进行10次随机采样得的10组相对重构误差,其平均值作为某一速度下的相对重构误差,同一加热棒不同速度的相对重构误差的平均值作为y坐标值,如图10所示。泄露位置从加热棒1到加热棒25的平均误差变化趋势,平均误差1是两个阶段速度0.01 m/s、0.02 m/s、……、0.06 m/s和0.1 m/s、0.15 m/s、……、0.6 m/s的平均误差,为10.79%;平均误差2是第二阶段速度0.1 m/s、0.15 m/s、……、0.6 m/s的平均误差,为6.82%。由此可见,第一阶段速度0.01 m/s、0.02 m/s、……、0.06 m/s重构造成的相对误差是比较大的,约占整体误差的40%,当泄露速度越大整体相对重构误差越小,这也从侧面映证了过程参数的数量级差异是造成误差的主要因素。

Figure 10. Average relative reconstruction error of 25 heating rods
图10. 25根加热棒的平均相对重构误差
6. 结论
本文开发了一种快速重构流场的方法。在该方法中,首先用CFD来提供一系列的流场样本,然后利用非负矩阵分解算法来获得流场样本矩阵基矩阵实现数据降维,最后基于多个测量数据利用逆解算法重构流场。分析表明:
1. 基于有限的过程参数测量数据,所提出的方法可用于重构复杂机械结构周围的流场。不同泄露情况下,都可以较为准确地重构流场,尤其是对于类似流场速度这类不存在较大数量级差异的过程参数,可以精确地重构流场。
2. 相对重构误差主要受基矩阵、采样率以及过程参数数量级的影响。在选取合适的基矩阵的前提下,采样率越低重构误差越大并且过程参数数量级的差异是误差的主要来源。
3. 在实际情况中,所提出的重构方法避免了多相流检测过程中复杂敏感场的计算,而且相较于CFD模拟方法和插值方法,重构所需的时间大幅缩减。
致谢
衷心地感谢本文所引用的这些优秀文章的作者,他们的文章提供很大的帮助;同时也感谢华北电力大学提供了一个研究创作的卓越平台。
基金项目
诚挚地感谢国家自然科学基金委员会赞助该研究(No 61571189,61871181)和国家外籍专家局对111引智计划的支持(ref:B13009)。