1. 引言
4球正交,球心间的垂心四面体构成勾股4态 [1] 的4个球心点(球)、6个两球间连线(勾股定理)、4个3球心所围面(面积勾股定理 [2] )、1个4球心所围体(四维体积勾股定理 [3] )均有各自的重心和垂心。这15组重心垂心按勾股4态,用4球半径表达的4种共球半径、球心坐标和欧拉线 [4] 间距关系如何?
2. 证明勾股四态的4个共球半径,球心坐标,欧拉线间距 均存在同构公式
4球正交,存在勾股4态,点、线、面、体4个共球,它们交4垂线同时交同态重心和垂心。4个共球球心与垂心共5点共线,即为垂心四面体的欧拉线,4个共球半径以及球心的坐标具有各自的同构的四元数公式。证明如下(为精简起见,各15组重心和垂心代数坐标符号均沿用“重心距离公式” [5]、“垂心距离公式” [6] 中所设)。
2.1. 按勾股4态的4个同态重心垂心共球半径及其球心坐标有 各自的同构公式
2.1.1. 勾股4态的4个同态重心垂心共球半径平方
的同构公式
定义:正交4球形成的勾股4态,仅用4球半径表达其存在4个同态重心垂心共球半径的平方等于维数平方分子4个重心球半径的平方与垂心球半径平方与维数减2的平方积之差。其公式为:
(1)
这里:
;重心球平方:
;垂心球平方:
。
2.1.2. 勾股4态的4个同态重心垂心共球球心坐标O1/n的同构公式 (即:欧拉线)
定义:勾股4态存在4个共球球心与1点垂心计5点共线的欧拉线,4共球坐标有同构公式为:2倍维数分子4球心坐标和与2倍的垂心坐标与2减维数积之差。其公式为:
 (2)
(2)
这里
的维数;
为共球心坐标;
为4球心,H为垂心;下标
为分坐标。
2.1.3. 勾股4态的4个同态重心垂心共球球心坐标O1/n与垂心H间距的同构公式(即:欧拉线)
定义:正交4球形成的勾股4态,存在4个同态重心垂心共球球心坐标距垂心距离为算术平均数。各共球与垂心间距得平方等于维数平方分子4与重心球半径与垂心球半径的平方差的积。其公式两边开方后为:
(3)
这里:
;重心球平方:
;垂心球平方:
。
例:
· 一维点态8点共球半径、球心坐标及距垂心距离:(8点共球在垂心四面体中为外接球。其半径的平方等于4球心至垂心距离平方和的四分之一,也等于4个重心球半径平方与垂心球半径平方差)。
其8点共球半径的平方,将
代入公式(1)为:
(4)
其8点共球球心坐标,将
代入公式(2)为:
(5)
这里:
, 本文下同。
本文下同。
其8点共球球心坐标与垂心H距离,将
代入公式(3)为:
(6)
· 二维线态20点共球半径、球心坐标及距垂心距离:(垂心四面体中交4垂线8点以及交4球心6条连线12点,总计20点共球,其半径和球心坐标同构重心球半径和重心坐标)。
其20点共球半径的平方,将
代入公式(1)为:
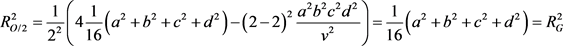 (7)
(7)
其20点共球球心坐标,将
代入公式(2)为:
(8)
其20点共球球心坐标与垂心H距离,将
代入公式(3)为:
(9)
· 三维面态12点共球半径、球心坐标及距垂心距离:(垂心四面体中为4垂线8点4平面重心4点,总计12点共球;半径是8点共球的三分之一)。
其12点共球半径的平方,将
代入公式(1)为:
(10)
其12点共球球心坐标,将
代入公式(2)为:
(11)
其12点共球球心坐标与垂心H距离,将
代入公式(3)为:
(12)
· 四维体态6点共球半径、球心坐标及距垂心距离:(垂心四面体中4垂线5点,其中垂心为4垂线交点,体重心1点,总计为6点共球)。
其6点共球半径的平方,将 n = 4 代入公式(1)为:
(13)
其6点共球球心坐标,将
代入公式(2)为:
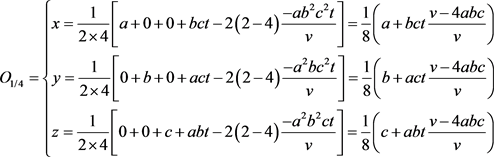 (14)
(14)
其6点共球球心坐标与垂心H距离,将 n = 4 代入公式(3)为:
(15)
上述关系见表1如下。

Table 1. List of 5 points collinear coordinates of Euler line and Pythagoras four states and radius of 4 common spheres
表1. 欧拉线5点共线坐标及其勾股4态4共球半径一览表
表内:这里:
;重心球平方:
;垂心球平方:
;
,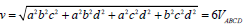 。
。
2.2. 验证勾股4态4共球半径、球心坐标及算术平均数的欧拉线
2.2.1. 验证勾股4态的4点同构的坐标间距为欧拉线算术平均数
假设上述公式正确:用2点距离公式验算欧拉线之间的距离如下:
· 勾股点态8点共球,球心O点至垂心H点至其间距用2点间距公式为:
两边开方公式(16)等于公式(6)为:
(16)
· 勾股线态20点共球球心  重心点,根据同态垂心与重心间距的平方,可以不用坐标,其间距等于重心球与垂心球半径的平方差。
,
重心点,根据同态垂心与重心间距的平方,可以不用坐标,其间距等于重心球与垂心球半径的平方差。
,
两边开方公式(17)等于公式(9)为:
(17)
· 勾股面态12点共球球心
至垂心H点间距,用2点坐标距离公式为;
两边开方公式(18)等于公式(12)为:
(18)
· 勾股体态6点共球球心
至垂心H点,用2点坐标距离公式为;
两边开方公式(19)等于公式(15)为:
(19)
根据公式(16)、(17)、(18)、(19)结果,验证了4点为垂心至8点共球球心2点共线,其间距为该2点间距为欧拉线算术平均数。
2.2.2. 验证勾股点态重心垂心共球半径及球心坐标(即垂心四面体的外接球 [7],或称垂心四面体8点共球)
证明了8点共球球面交4垂线共8点共球,其中:8点共球交正交4球心,该球心与4球重心、4球垂心共点,因此该共球在这里称“勾股点态一维重心垂心共球”,共球半径的平方等于正交4球心至垂心距离的平方和的四分之一,也等于重心球半径与垂心球半径的平方差的4倍。
假设公式(4),公式(5)成立,勾股点态重心垂心共球半径及球心坐标见表1,将4垂线参数方程公式(20)与8点共球半径和球心的球面方程联立公式(21),即得4垂线交该球面8点,其中4点为正交4球的球心、与4球重心和垂心共点:
验证如下:
例:
· 过A点和垂心H点2点的垂线参数方程为:
(20)
8点共球半径的平方见:公式(4);球心为O见:公式(5),立球面方程为:将公式(20)代入公式(16)左右式相减:
(21)
得
将
代入公式(20)得8点共球与过A点垂线的2交点坐标为:
 与
与
同理我们可得:
· 过B点和垂心H点2点的垂线参数方程为:
(22)
代入共球球面方程:
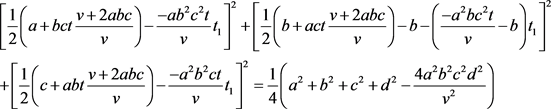 (23)
(23)
得
将参数
代回公式(22)过B点垂线2交点坐标为:
与
· 过C点和垂心H点2点的垂线参数方程为:
(24)
代入共球球面方程:
(25)
得
将参数
代回公式(24)过C点垂线2交点坐标为:
与
· 过D点和垂心H点2点的垂线参数方程为:
(26)
代入共球球面方程:
(27)
得
将参数
代回公式(26)过D点垂线2交点坐标为:
与 
因此,验证8点共球半径的平方公式(4),以及8点共球球心坐标公式(5)成立。且证明了8点共球球面交4垂线共8点共球,其中:8点共球交正交4球心,该球心与4球重心、4球垂心共点,因此该共球在这里称“勾股点态一维重心垂心共球”,共球半径的平方等于正交4球心至垂心距离的平方和的四分之一,也等于重心球半径与垂心球半径的平方差的4倍。
2.2.3. 验证勾股线态20点共球半径及球心坐标(共球面与6棱和4垂线各交2点)
证明“勾股线态二维重心垂心共球”球面交4垂线以及6棱共20点共球,20点共球球心为四维重心;共球半径的平方等于四维重心球半径的平方。
假设公式(7)、公式(8)成立,勾股线态重心垂心共球半径及球心坐标见表1,将4垂线参数方程与20点共球半径和球心的球面方程联立,即得4垂线交该球面8点,同理,将6棱线参数方程与20点共球球面方程联立,可得共球球面交6棱,各棱重心垂心2点,合计12点共球交点,合计20点共球。
验证1:4垂线与该共球交8点:
例:
· 过A点与H垂心的垂线的参数方程见:公式(20)代入公式(28)
20点共球球面方程为:
(28)
将得到的参数:
代入过A点垂线参数方程
公式(20)得2交点为:
和
· 过B点与H垂心的垂线的参数方程见:公式(22)代入公式(29)
20点共球球面方程为:
(29)
将得到的参数:
代入过B点垂线参数方程公
式(22)得2交点为:
和
· 过C点与H垂心的垂线的参数方程见:公式(24)代入公式(30)
20点共球球面方程为:
(30)
将得到的参数:
代入过C点垂线参数方程公
式(24)得2交点为:
和
· 过D点与H垂心的垂线的参数方程见:公式(26)代入公式(31)
20点共球球面方程为:
 (31)
(31)
将得到的参数:
代入过D点垂线参数方程
公式(26)得2交点为:
和
验证2:6棱重心与该共球交6点:
· 过A点与B点的AB棱的直线的参数方程为:
(32)
将直线参数公式(32)代入20点共球球面方程公式(33)求参数
:
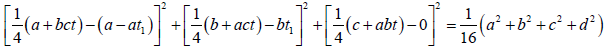 (33)
(33)
将得到的参数:
代入过A、B直线参数方程公式(32)得2交点为:
和
该共球球面与AB棱交的2点分别为:二维AB直线的重心和垂心。
同理:我们可以得到该共球球面与其它5棱的重心和垂心相交。
∵该共球球心与四维重心共点,而6棱重心为二维重心;
∴其间距可以使用重心间间距可不用使用坐标,直接使用重心球间距公式 [5] 计算。
例:
·
同理可得其它5点二维重心与共球球心间距为:
·
·
·
·
·
验证3:6棱垂心与该共球交6点:用2点坐标距离公式可得:
例:
·
·
·
·
·
·
通过上述验证:20点共球球心以及半径验证成立。
(其中:二维棱12点:各棱重心与垂心2点,并与4垂线8点:各垂线交2点共,合计20点共球。)
2.2.4. 验证勾股面态12点共球 [8] 半径及球心坐标(即4面重心垂心各2点;以及4垂线各另1交点)
证明“勾股面态三维重心垂心共球”球面交4垂线8点(含4面垂心)以及4面重心共12点共球,三维面态12点共球半径等于一维点态8点共球半径的三分之一。
假设公式(10)、公式(11)成立,勾股面态重心垂心共球半径及球心坐标见表1,将4垂线参数方程与12点共球半径和球心的球面方程联立,即得4垂线交该球面8点;将各面4点重心与12点共球球心按2点坐标距离公式验算,可得勾股面态12点共球及半径。
验证1:4垂线与该共球交8点:
例:
· 过A点与H垂心的垂线的参数方程见:公式(20)代入公式(34)
12点共球球面方程为:
(34)
将得到的参数:
代入过A点垂线参数方程公式(20)得2交点为:
和
这里:
为A点对平面的垂心, 。
。
· 过B点与H垂心的垂线的参数方程见:公式(22)代入公式(35)
12点共球球面方程为:
(35)
将得到的参数:
代入过B点垂线参数方程公式(22)得2交点为:
和
这里:
为B点对平面的垂心,  。
。
· 过C点与H垂心的垂线的参数方程见:公式(24)代入公式(36)
12点共球球面方程为:
(36)
将得到的参数:
代入过C点垂线参数方程公式(24)得2交点为:
和
这里:
为C点对平面的垂心,
。
· 过D点与H垂心的垂线的参数方程见:公式(26)代入公式(37)
12点共球球面方程为:
(37)
将得到的参数:
代入过D点垂线参数方程公式(26)得2交点为:
和 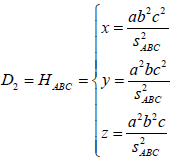
这里:
为D点对平面的垂心,
。
通过上述验证:12点共球球心以及半径验证成立。
(其中:三维面8点:各面重心与垂心2点,并与4垂线2点中的另1点,4垂线4点;合计12点共球。)
2.2.5. 验证勾股体态6点共球半径及球心坐标
证明“勾股面态四维重心垂心共球”球面交4垂线5点(含1点体垂心)以及1点体重心共6点共球,四维体态6点共球半径平方与6点共球球心至垂心间距平方相同:等于一维点态球心O至4维体态垂心间距的四分之一。
假设公式(13)、公式(14)成立,勾股体态重心垂心共球半径及球心坐标见表1,将4垂线参数方程与6点共球半径和球心的球面方程联立,即得4垂线交该球面5点;将1点体重心与6点共球球心按2点坐标距离公式验算,可得勾股体态6点共球及半径。
验证1:4垂线与该共球交5点:
例:
· 过A点与H垂心的垂线的参数方程见:公式(20)代入公式(38)
6点共球球面方程为:
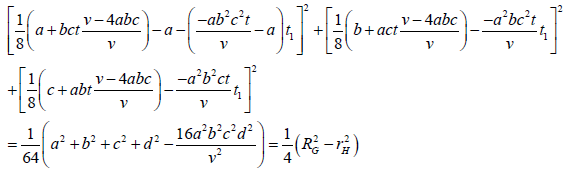 (38)
(38)
将得到的参数:
代入过A点垂线参数方程公式(20)得2交点为:
和
· 过B点与H垂心的垂线的参数方程见:公式(22)代入公式(39)
6点共球球面方程为:
(39)
将得到的参数:
代入过A点垂线参数方程公式(22)得2交点为:
和
· 过C点与H垂心的垂线的参数方程见:公式(24)代入公式(40)
6点共球球面方程为:
(40)
将得到的参数:
代入过A点垂线参数方程公式(24)得2交点为:
和 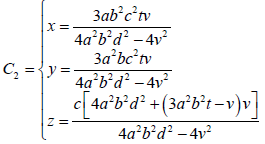
· 过D点与H垂心的垂线的参数方程见:公式(26)代入公式(41)
6点共球球面方程为:
(41)
将得到的参数:
代入过D点垂线参数方程公式(26)得2交点为:
和
验证2:4维重心与该共球球心2点坐标距离
通过上述验证:6点共球球心以及半径验证成立。
(其中:4维体6点:体重心与垂心2点,并与4垂线2点中的另1点,4垂线4点;合计6点共球。)
3. 总结
通过上述验证,证明了4球正交形成的勾股4态 [1],存在点、线、面、体4个共球,它们交4垂线同时交同态重心和垂心。4个共球半径公式(1)成立、4个共球球心坐标公式(2)成立、4个共球球心坐标与垂心H距离公式(3)成立。且得出如下结论。
3.1. 一至四维重心与垂心4个共球半径符合公式(1)
一至四维重心与垂心4个共球半径的变化规律符合公式(1),均在重心球与垂心球半径间。
3.2. 一至四维重心与垂心4个共球球心坐标符合公式(2)
一至四维重心与垂心4个共球球心坐标的变化规律符合公式(2),为4球球心坐标与垂心坐标间。
3.3. 一至四维重心与垂心4个共球球心坐标距垂心坐标间距符合公式(3)
一至四维重心与垂心4个共球球心坐标距垂心坐标5点共线,即欧拉线,4个共球球心距垂心间距为算术平均数。