1. 引言
随着经济社会的发展,越来越多的城市会举办一些大型活动来促进城市之间的交流和发展,比如上海的进博会、杭州的互联网大会、以及各地演唱会、体育赛事等。这一方面会提升城市品牌建设,但是另一方面也给城市交通管理带来压力。
大型活动产生的交通流一般具有瞬时性、高密度和方向性 [1],用户的出行需求在短时间内呈现空间集中性。同时,用户偏好的出行方式选择行为会使得道路流量增多,在这种情况下,供需矛盾不能单纯靠增加交通资源的供给来解决,有必要从交通需求管理的角度来调整用户的出行需求。考虑到大型活动周边停车场资源的有限性,从停车管理的角度来影响用户的出行需求可以作为一个出发点,在解决停车矛盾的同时可以缓解活动周边的道路拥堵。
大型活动的停车问题可以描述为用户的停车场选择问题,用以预测交通流在网络中的分布情况。吕能超提出了基于logit的效用模型来描述用户的停车场选择行为,分析了不同停车价格对于用户选择行为的影响,并探究了不完全诱导信息发布的优化方法 [1]。Zhen和H. M. Zhang完善了停车场选择均衡模型,考虑了停车容量、停车收费和停车场与目的地之间的可达性因素 [2]。除了停车定价,停车券分配问题也得到很多学者的研究。Zhang等考虑了小汽车和公交车两种出行方式,研究了早高峰时期存在瓶颈路段的网络中,终点停车容量有限时的停车券分配方法 [3]。Liu和Yang研究了不同的停车预定有效期对于缓解早高峰拥堵的效率,并得到了最优的预定比例 [4]。此外,Sarasua从交通仿真的角度研究了不同的交通组织方式对于停车分布的影响,开发了基于GIS的交通仿真系统 [5]。但是,很少有文章将出行方式选择和停车场选择结合起来,从系统最优化的角度,研究大型活动场景下的停车管理问题。
考虑到大型活动的暂时性,以及用户对一次性消费支出的价格敏感度比较低,停车定价策略的非强制性使得其在实际应用中未必可以很好地调节用户的出行需求。另一方面,大型活动周边的停车资源一般是比较集中的,且有容量限制,难以满足所有潜在的小汽车出行需求,活动组织方希望用户更多的选择公共交通出行。在这种情况下,本文不考虑终点停车场的选择问题,主要研究用户的出行方式选择,并且通过停车换乘来描述用户在换乘停车场和目的地停车场之间的选择行为。因此,本文的重点就是综合考虑道路交通和公共交通网络,研究如何通过停车券的分配来改变用户的出行方式选择决策,从而使交通流在道路和公共交通网络上呈现相对均衡分布,提高公共交通分担率,缓解活动周边道路拥堵,进而提高系统的出行效率。
首先,本文分析影响用户出行方式选择的因素,考虑小汽车(包括私家车和出租车)、地铁和停车换乘三种出行方式,建立多元logit选择模型,进一步构建考虑终点停车约束的多用户方式划分均衡模型。然后,将大型活动停车组织的规划者和出行者分别作为上层模型和下层模型的决策者,利用双层规划模型描述停车券分配策略和用户出行方式选择的博弈过程。其中,下层规划是考虑停车券分配的多用户方式划分均衡模型,上层规划的目标是最小化系统的总体出行成本,并设计相应的算法进行求解,得到最优的停车券分配策略。最后,通过算例验证模型的有效性。
2. 模型建立
考虑到目的地停车资源的有限性,以及地铁在出行起点的可获得性,组合出行成为一种重要的出行方式。因此,本文考虑全程小汽车、地铁、停车换乘三种交通出行方式,其中,停车换乘先是小汽车出行,中途换乘地铁完成整个出行过程。出行者综合考虑三种出行方式的出行时间成本、停车资源约束、出行费用、舒适度等因素进行出行方式选择,在每一种出行方式下,出行者通过路径选择达到交通均衡状态。同时,大型活动停车组织的规划者在用户出行方式和路径选择均衡的基础上,以最小化系统总运行成本为目标,制定停车券分配策略。此外,由于大型活动的特殊性和暂时性,用户的出行需求一般是确定的,不会因为出行成本等因素放弃出行,出行需求只会在不同的出行方式之间转移。
停车券分配问题(如图1)是一个双层规划问题。上层规划是停车组织的规划者在用户选择行为的基础上制定停车券分配策略,以实现系统总出行成本最小;下层是用户根据具体的停车券策略做出最优的出行选择,上下层之间的策略相互影响,均衡时即得到双层规划问题的解。

Figure 1. Parking permit distribution model based on user equilibrium
图1. 基于用户均衡的停车券分配模型结构
假设一个交通网络为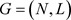 ,存在3种出行方式:全程小汽车、全程地铁和停车换乘,分别为
。其中,N为所有节点集合,L为连接节点的路段集,G包含小汽车出行子网络
,地铁子网络
,以及换乘网络
(虚拟网络),用来表示用户换乘行为。本文假定每一个出行产生区到目的地之间的换乘地点是确定的,在地铁站点附近,不考虑换乘停车场内部的选择问题,同时假定换乘停车场的资源是充足的。R为网络中所有起点集合,
,s为目的地,在本文研究中只有一个目的地,rs表示从起点r出发到目的地s。
,存在3种出行方式:全程小汽车、全程地铁和停车换乘,分别为
。其中,N为所有节点集合,L为连接节点的路段集,G包含小汽车出行子网络
,地铁子网络
,以及换乘网络
(虚拟网络),用来表示用户换乘行为。本文假定每一个出行产生区到目的地之间的换乘地点是确定的,在地铁站点附近,不考虑换乘停车场内部的选择问题,同时假定换乘停车场的资源是充足的。R为网络中所有起点集合,
,s为目的地,在本文研究中只有一个目的地,rs表示从起点r出发到目的地s。
2.1. 出行方式选择模型
在大型活动的出行过程中,出行者从起点出发到达终点有多种出行方式可以选择,而对应每一种出行方式又可能有多条路径可以到达。因此,出行者的出行选择过程主要包括两个方面:一是出行方式的选择决策;二是指定出行方式下的路径决策。每一种交通工具为出行者带来的出行效用即旅行费用并非是固定不变的,因此,每一种交通方式对应的交通需求量是变化的。路径旅行时间会影响出行方式的选择,出行方式选择的结果反过来也会影响路径旅行时间,二者相互影响又相互制约,共同决定网络中所有用户的出行过程。
实际中,各种出行方式的特点和优势各不相同,小汽车出行具有较高的可达性、舒适性,但出行费用比较高,且受限于终点的停车状况;地铁出行经济环保,但是可达性和舒适性比较差;停车换乘可以综合二者的特点。综合分析,本文假定影响用户出行方式选择的主要因素包括:1) 不同出行方式的出行时间;2) 出行方式对用户的吸引度(以出行时间为单位);3) 活动周边的停车约束情况;4) 个体属性诸如出行者的收入、价格敏感程度、时间敏感度等因素。
本文采用多元logit选择模型来描述出行时间、出行方式吸引力、停车约束等出行方式选择特征和其他社会经济特征对于选择不同出行方式的效用函数所产生的影响,假定效用随机误差项相互独立且服从参数为(0,1)的双指数分布 [6],每个出行者按照效用最大化的原则出行。用I表示用户类型,那么从起点r出发到终点s的出行者i选择出行方式j的概率
用多元logit的形式可以表示为,
(1)
其中,
为平衡状态下用户i选择出行方式m从起点r到终点s的路网行驶时间,
是rs之间终点的停车流量达到其能力时所产生的成本,
表示小汽车出行需额外付出停车成本,
是出行方式m对用户的吸引力,
是待估参数,表示第i类型的出行者对出行方式的权重,
取值越大,说明出行方式的吸引力对于出行者的选择影响比较大。
为大于0的常数,其值与随机误差项的方差成反比,用来调节方差。
2.2. 下层多方式网络均衡模型
城市多方式交通网络的流量分配是出行者对于出行方式和路径选择之后的结果。对于某一种出行方式,出行者是通过广义费用最小化的原则进行路径的选择,均衡时,没有出行者可以通过改变路径来使出行成本下降。对于小汽车子网络,路段旅行时间是路段流量的增函数;对于地铁子网络,其流量越多,用户等待的时间就越长,可以将两个站点之间的广义出行时间理解成其流量的增函数。对于停车换乘(如图2所示),其路径均衡包括两部分,
,每一部分被选择的路径时间都是最小均衡时间。
为虚拟路段表示换乘行为,连接小汽车子网络和地铁子网络,实现换乘流量从道路网络向地铁网络的流转,进而实现停车换乘方式
的路径选择。对于换乘路段,出行者在停车过程中的时间消耗就是虚拟路段的旅行时间,当换乘流量增多时,停车位的搜寻时间增大,相应地表示为路段旅行时间增大,即虚拟路段的阻抗函数是关于该OD对停车换乘流量的增函数。
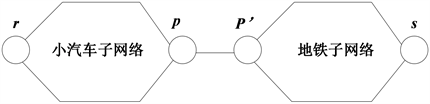
Figure 2. Park-and-ride network structure
图2. 停车换乘网络结构图
考虑用户的异质性,针对用户出行方式选择行为,城市交通网络流量分配问题可以表示为如下的数学规划模型:
(2)
(3)
(4)
(5)
(6)
路径和路段关系如下,
(7)
(8)
换乘路段将小汽车子网络和地铁子网络连接起来,实现停车换乘方式从
的路径选择行为,那么(7) (8)可以合并为,
(9)
其中,
为OD对rs之间路径k上第i类用户的出行量,
、
为换乘路径流量;
为OD对rs之间选择出行方式m的所有路径集合,
,
分别是停车换乘中小汽车和地铁子网络中的路径集合;
为路段l上的流量;
表示路径和路段之间的关系变量,当路段l在连接rs之间的路径k上则
,否则
。
为rs之间出行方式m的交通流量,
表示rs之间出行方式m中第i类用户的流量,
有
;
为终点s分配给起点r的停车券数量;
为路段通行时间,是路段流量的增函
数;
为起点r的出行需求量。约束(5)说明rs之间小汽车出行量应该小于等于其间的停车券数量。此外,由于大型活动一般只有一个目的地,所以模型中S只有一个。
通过定义拉格朗日函数,可以证明上述规划与基于logit方式选择的用户均衡条件等价 [7],且具有唯一性。
2.3. 上层停车券分配模型
上层规划是将终点的停车位在各个起点之间进行分配,即停车券的具体发放策略问题,目标函数是最小化整个交通网络的总出行成本,数学规划为,
(10)
(11)
(12)
是上层规划的输入变量,为终点分配给起点r的停车券数量,
是下层规划问题的解,是关于
的函数。约束(11)保证终点分配给所有起点的停车券总量应不超过其自身的停车容量(
)限制。
3. 求解算法
双层规划一般是NP-hard问题,即使上层和下层模型均是凸规划,整个双层规划仍然有很大的可能是非凸的,因此,其最优解不具备唯一性。此外,双层规划问题的非凸性以及非处处可微性,使得精确算法求解比较困难。近年来,人工智能算法,比如模拟退火算法、粒子群算法等,在交通问题领域得到越来越多的应用,这类算法对目标函数的要求比较小,算法简单,且容易实现。
模拟退火算法(Simulated Annealing, SA)是基于物理中固体物质退火过程的智能随机优化算法,已经广泛应用于全局最优解的求解中。其以一定的概率接受一个比较差的解,因此有可能会跳出局部最优,得到全局最优解 [8]。本文采用模拟退火算法并借助分层迭代的思想求解该问题,即通过全局优化工具求解下层用户均衡模型,用模拟退火算法在上下层之间进行反复迭代,最后逐渐逼近双层规划的最优解。
由于模拟退火算法求解的是无约束问题(只包含决策变量自身约束),所以利用一个辅助优化问题来处理上层规划的约束条件 [8]:
(13)
约束同(11)(12)。
向量
代表一个停车券分配策略。式中,
为模拟退火算法随机产生的上层决策变量取值,不确定其是否满足上层约束条件,暂称其为试探点。
为Euclidean范数。通过求解该辅助优化问题,可以将随机产生的试探点变成满足上层约束的点,这样可以避免罚函数处理上层规划的约束条件 [8],以提高算法有效性和全局最优解的可靠性。双层规划求解的模拟退火算法的具体步骤如下:
步骤1:给定初始解
,初始温度
,终止温度
和内循环次数为LN,其中N为决策变量的个数。令外层循环次数
,
,内层循环次数
。若
满足上层规划的约束条件(11)、(12)式,取
,否则令
,求解问题(13)得到最优解
,以
为上层决策变量取值,求解下层规划问题的最优解
,进一步得到
和
,并计算
。
步骤2:在温度
下,进行如下操作:
1) 利用均匀分布进行随机扰动,产生一个新的试探点
。若
满足上层约束,则取
,否则令
,求解问题(13)得到最优解p。以p为上层决策变量取值,求解下层规划,得到最优解
,计算下层目标函数值
。
2) 若
,则接受p,令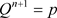 ,
,
。否则,以一定的概率决定是否接受新解:产生一个(0,1)上均匀分布的随机变量
,计算在当前迭代点和温度
下接受点p的概率
,
,
。否则,以一定的概率决定是否接受新解:产生一个(0,1)上均匀分布的随机变量
,计算在当前迭代点和温度
下接受点p的概率
。若
,则令
,
,
;否则,
,
,
。
3) 更新
,若
时,继续下一次的扰动和接受过程,即执行1) 2)过程。否则,转到步骤3。
步骤3:若
,则以
为上层规划问题的最优解,将
输入下层规划得到
,即得到该双层规划问题的最优解。否则,按下式产生一个新的温度:
,
是一个接近1的常数。令
,
,
,转向步骤2。
4. 算例分析
假设一个如图3所示的交通网络,共16个节点,22条边。其中有3个出行需求产生区(节点1、2、3),大型活动所在地为节点10,节点5为换乘中心,小汽车出行的用户可以由此换乘地铁,(5,15)为换乘路段。本节内容利用该交通网络求解给定参数下的最优停车券分配策略。
4.1. 参数设置
在本算例中,路段阻抗函数采用BPR形式,如公式(14)所示。对于小汽车路段
,
为路段l的自由流时间,
为路段l的通行能力,
均为待定参数,本算例中取默认值
。对于地铁路段
,
可以理解为地铁票价(以时间为计算单位),
是反映地铁等待时间和车厢内拥挤程度的参数,
取值同上 [9]。对于换乘路段
,其时间主要包括停车位寻找时间、步行时间、以及等待时间,其中停车位寻找时间主要与换乘车辆数、停车位数量有关,换乘路段的交通阻抗也可以用BPR函数来表示,
表示自由换乘时间,
为停车场容量,
表示换乘车辆数,取
[10]。道路网络上,交通流的分配以车辆为单位,而地铁网络上通过用户进行流量分配。假设一辆车只乘坐一名用户,道路和地铁网络统一以乘客为单位进行流量分配。路段相关参数如表1所示,自由流时间单位为(分钟),路段容量单位为(辆∙h−1)。
(14)
设起点1的出行总需求
为4500,起点2和起点3的出行总需求分别为4500和3500,参数
取值为1。
4.2. 算例结果和效率分析
假定网络中存在两类用户,每个起点中各类用户所占的比例均为50%,第一类用户比较看重出行方式的舒适度、便利性(即出行方式的吸引力);第二类用户对出行方式的吸引力敏感度比较低。设
,
,活动周边停车位供给能力为4000,其他参数设置同前文。本文程序采用MATLAB编写,并在Intel Core i7 2.70 GHz计算机运行。
以终点分配给每个起点的停车券数量
为决策变量,在问题的可行域内随机选择一个初始解,得到的最优停车券分配结果为(588,0,3412),即将终点的4000个停车资源分配给三个起点的数量分别是588、0和3412。这说明在系统最优条件下,大型活动停车组织规划方倾向于将终点有限的停车资源配置到公共交通不发达的地区,同时减少道路拥堵区域的小汽车出行。在该策略下的均衡出行结果如表2所示,第一类用户更倾向于选择小汽车和停车换乘方式,第二类用户则更多是地铁出行。

Table 2. Traffic equilibrium results with optimal parking permit distribution
表2. 最优停车券分配下的交通流方式划分
算例结果表明,在最优停车券分配下,系统总的出行成本为11,272小时,相比没有停车约束下19,341小时,总成本降低了近72%,说明停车券分配策略可以在很大程度上减少系统出行成本。两种情况下不同出行方式对比如图4所示,在最优停车券分配策略下,小汽车、地铁和停车换乘方式所占的比例分别是32%、54%以及14%,使用和部分使用公共交通的流量占总出行需求的68%。另一方面,在没有停车约束的情况下,小汽车、地铁和停车换乘方式占总出行需求的比例分别为65%、15%以及20%。由此可见,停车券分配策略可以极大地提高公共交通的使用率,限制小汽车方式的出行,尽管转移到地铁的出行者会增加地铁出行时间,但是总的出行成本是减少的。通过综合考虑每一个出行产生区的交通资源供给情况,以系统最优化为目标,合理配置终点的停车资源,通过停车券来影响用户的出行方式选择行为,进而将瓶颈路段流量过渡到公共交通,减少路段拥堵,提高系统的出行效率。
但是,值得一提的是停车券分配策略只能优化用户的出行方式选择行为,没有实现用户的路径选择优化,用户在进行路径选择时,仍然只考虑了自身的出行时间,没有考虑到自身的选择给网络中其他用户所带来的影响。路段拥堵收费或者补贴是将出行者外部效用内部化的有效方法,通过对比较拥堵的路段进行收费,或者是补贴出行潜力没有被开发的路段可以提高系统效率。当收费路段已经确定时,拥堵定价问题的决策变量就是收费路段上的收费额度,该问题也是一个双层规划问题,已有较多的研究,比如Zhang [11] 此处不做赘述。

Figure 4. Traffic flow of different travel mode
图4. 各出行方式交通流
5. 结论
本文研究了大型活动中用户的出行方式选择行为,考虑了小汽车、地铁和停车换乘三种出行方式,其中用户一般倾向于选择小汽车这种舒适度比较高的出行方式。这种用户偏好的出行方式选择行为会造成交通资源的不均衡利用,表现在交通网络上就是道路网络的严重拥堵,同时公共交通的利用率低,造成整个系统出行效率低下。鉴于大型活动周边的停车资源一般是有限的,本文从停车管理的角度出发,提出了停车券分配策略来调节用户的出行方式选择决策,建立了双层规划模型。上层决策者为大型活动停车组织的规划方,将活动周边的停车资源在不同起点进行分配,下层规划是用户在给定停车券分配方案下的出行方式、出行路径选择模型。数值实验表明,停车券分配策略可以综合考虑不同区域道路网络和公共交通的资源供给情况,平衡交通流在不同方式之间的分配,缓解活动周边路段拥堵,极大地提高公共交通的分担率,保障道路网络和公共交通网络整体的运行效率。
伴随着互联网、物联网和各种人工智能技术的发展,各种服务器以及架构在其上的数据库软件可以实现停车券的智能分配;基于移动端的应用程序利用定位技术以及图像识别等技术可以实现停车券预约、交易、使用等过程。另外,停车券交易系统允许停车券在一定区域内自由交易,提高用户出行方式选择的灵活性。
本文所研究的大型活动反映到现实中,可以是国际论坛、演唱会、赛事等大型活动,也可以是节假日热门景点、场所。对于不同的出行场景,需要考虑的用户选择行为是不一样的,不同出行方式的吸引程度也应不同,模型中的参数需要进行相应的设置。此外,本文的模型假定比较严格,没有考虑换乘停车场的容量约束和选择问题,有待进一步完善。