1. 引言
声波在含气泡液体中的传播,会受到液体中气泡的影响,该影响取决于气泡的含量、气泡大小、声场的频率及强度等多种因素 [1] [2] [3]。一般表现有两种情况,其一是气泡在声场的作用下做线性振动,气泡对声场的传播起散射作用;其二是气泡在声场的作用下做复杂的非线性振动,如空化现象 [4] [5] [6] [7],对于液体中气泡的空化现象的发生,一般情况下会取决于气泡的含量、气泡的大小及声场的情况。在第二种情况下,气泡的非线性振动会导致气泡克服气泡壁与液体间的粘滞阻力做功、气泡与液体间出现热传导及引起气泡的次级声辐射等现象 [8] [9] [10] [11],而所有这些现象均会引起液体所传播声场的能量发生较剧烈的变化 [12]。声波在含气泡液体中传播时,气泡的出现会产生许多可供应用的物理及化学效应,但气泡并不是越多越好,因为随着气泡的增加,发生空化气泡的数量增加,在单位体积里声场能量的衰减也会加快,从而会导致液体中声场的强度及分布发生变化。沿着声场传播的方向,如果能量衰减过快的话,则会导致能够使气泡发生空化的区域变小,反而会影响液体中气泡空化的发生。本文考虑了气泡在空化过程中对声场能量带来的损失,结合声场的能量传播建立了含气泡液体中声场的能量传播模型,利用该模型研究了气泡对液体中声场能量传播的影响,并对相关的结果进行了分析,发现根据所提出的研究思路可以较容易地用来对含气泡液体中声场的传播进行建模并进行数值分析。在研究的过程中,我们只考虑气泡空化对声传播带来的影响,忽略了液体本身对声传播的衰减以及气泡对声场散射的影响,同时假设气泡大小相同且在液体中均匀分布。
2. 声场能量传播模型
2.1. 气泡振动的能量模型
单个气泡的物理模型我们选用文献 [2] 中的R-P方程描述如下:
(1)
式中
表示液体密度,R表示气泡的半径,P为气泡所在位置当气泡不存在时的压强 [13] [14],式中的圆点表示对时间的微分,常数
表示周围液体的动态粘滞系数,
表示液体的环境压强,常数
是气液界面的表面张力系数,
示气泡内部的压强,
(2)
(3)
设气泡在振动过程中某时刻的体积变化为
,对(1)式两侧同时乘以
并整理得到
(4)
对于上式来说,等式左边表示气泡在振动过程中声场对气泡所做的功,等式右边表示泡内气体、液体表面张力、液体粘滞阻力及泡外的液体静压力对气泡所做的功。(4)式体现了在气泡振动过程中上述各部分能量之间的平衡。(4)式的整个右半部分就可以用来描述在气泡振动过程中驱动声场由于单个气泡振动带来的能量损耗。在此需要说明的是,为了描述问题简单期间选用R-P方程描述气泡的振动,所以在(4)式中没有涉及到泡内气体的内能、气泡振动的声辐射、气泡与液体间的热传导等能量。
2.2. 声场能量传播模型
声场在液体中传播的过程中,声场能量沿着声场传播的方向由近及远地传播,如果没有能量损失的话,则声场的振幅恒定,否则,伴随声场能量的衰减,声场的振幅会随之减小。将含气泡液体沿声传播方向(中此只考虑声场的一维传播)划分为多个体积元,在每个体积元内分布等量气泡,由于气泡在声场的作用下振动,引起声场能量损失,所以传递到下一个体积元的声能量就等于前一个体积元中声场能量减去气泡振动损失的能量,根据以上的思路,来建立声场能量传播模型,研究声场的振幅。
假设声场为
,在声场中取一体积元
,体积元内的总的声能量为
(5)
上式中
为液体振动速度。假设液体中气泡的体积含量为
,根据(4)式,单个气泡振动损失的声场能量为
,则在单个体积元中损失的声场能量为
(6)
传递到下一个体积元的声能量为
(7)
根据(4-6)式有
(8)
所以,可以通过(8)来研究含气泡液体中声场的传播情况。
3. 数值模拟分析
根据上面建立的能量传播模型,我们对单个气泡振动过程中损耗的机械能及声波在传播过程中受气泡的影响进行数值模拟。涉及到的参数如下:
,
,
,
,
,
。
图1中图1(a)图展示了气泡在振动过程中气泡半径随时间变化的情况,图1(b)图展示了单个气泡在振动过程中的机械能随时间变化的情况,图1(c)图表示了声场在气泡振动过程中的机械能损失的情况。由图1所示的情况分析可知,单个气泡的机械能与气泡所处的状态有很大的关系。从图1(a)中可以看出,当气泡的体积变化较剧烈时,其机械能的变化也就比较明显,特别是当气泡发生空化时,气泡机械能剧烈增加,其变化最为明显;在其后的振动过程中,每一次气泡的压缩,其机械能均有较明显的浮动,只不过其幅值相对较小。这一点很容易理解,气泡体积变化时,伴随着的是泡壁的速度变化、气泡克服液体表面张力做功的变化、气泡克服液体粘滞阻力做功的变化等,而所有的这些均会影响到气泡的机械能情况。由图1(c)中可以看出,声场损失的机械能有一个先减小后增大的过程,当增大到一定程度后其量值变化就不太明显,而这一变化对应的是气泡的半径先增大后减小然后在附近振动。所以可以认为气泡的空化过程对声场的机械能损失是最大的,如图中气泡半径第一次快速缩小时声场的机械能损失情况;当空化现象不明显时,气泡的振动趋于稳定,声场的机械能损失也就同气泡大小变化类似,在某个平衡位置附近振动,总的损失量不再明显地变化。另外严格来说,气泡内气体的内能、泡壁与气体的热传导、气泡振动的声辐射等也会影响声场的机械能,由于我们所选取模型的原因,这些影响没有明显地表现出来,但对于由气泡、液体及声场构成的这个系统来说,气泡振动的机械能,泡内气体及液体的内能变化以及气泡振动的声辐射等能量均来源于驱动声场的机械能,它们的出现均会导致驱动声场的机械能衰减。
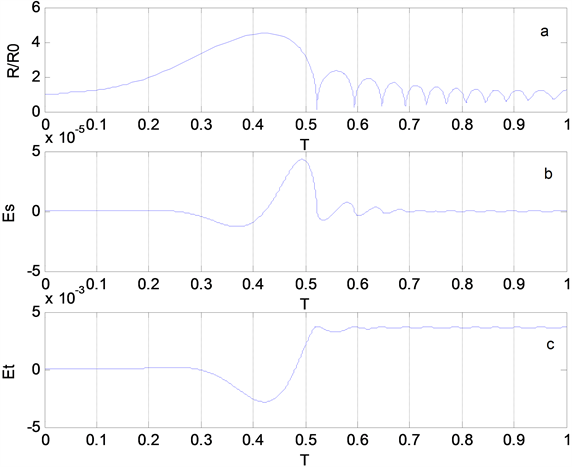
Figure 1. Bubble radius, mechanical energy and mechanical energy loss of driving sound field change with time
图1. 气泡半径、机械能及驱动声场机械能损失随时间变化的情况
在模拟的过程中,我们近似地认为如果声场的振幅值小于气泡空化所需的Black域值 [15],则认为气泡不会发生空化,声场的传播不受液体中气泡的影响。这样的话可以很明显地看到气泡空化对声场传播的影响。图中三组声波传播的时间相及频率相同,其振幅的区别通过
显示,气泡体积含量的多少通过
显示。从图中可以看出,三组声波传播图像中声场传播图像虽不尽相同,但在传播过程中其振幅均有一个快速减小的过程,然后才做等幅振动传播。分析其振幅快速减小的原因是由于液体中气泡的空化导致,气泡的空化导致声场机械能快速衰减,从而致使声场的振幅减小,而此后声波振幅小于气泡空化所需的Blacl域,气泡不再空化,所以对声场传播不再产生大的影响,所以声场做等幅振动。这个结果说明气泡空化对声场传播的影响仅是在距声源很近的一个微小的区域,过了这个区域,声场的传播不受液体中气泡的影响,换名话说就是气泡发生空化的区域仅在距声源附近一个微小的区域。另外,从图2中还可以看出气泡空化区域的影响因素。在声场及气泡大小一定的情况下,气泡越多,气泡能够发生空化的区域就会越小;气泡情况相同的情况下,驱动声场的振幅越大,气泡发生空化的区域就会越大。所以从这角度来说,要提高含气泡液体中气泡发生空化的区域,其一个可供的选择就是提高驱动声场的振幅;而对于气泡含量的选取则要根据实际情况来选择,因为如果气泡过少,则会影响到气泡空化产生的效果,如果气泡过多,则会导致气泡发生空化的区域减小。
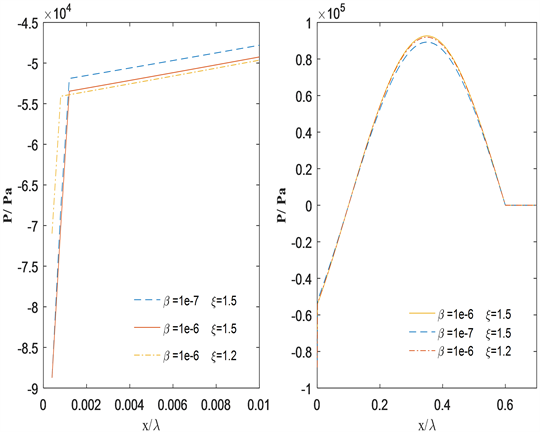
Figure 2. Influence of bubble content and sound field amplitude on sound field propagation
图2. 气泡含量及声场振幅对声场传播的影响
4. 结论
本文提出一种利用能量传播建立声传播模型的思路。将气泡的振动及声场的机械能结合起来建立声传播模型,研究声波在含气泡液体中传播过程中由于气泡振动引起气泡及驱动声场的机械能的变化情况。并利用该模型对由于单个气泡空化引起气泡的机械能变化情况、驱动声场的机械能损失情况及在该模型下气泡振动对驱动声场传播过程的影响进行了数值模拟。对于气泡来说,气泡在振动过程中由于其体积发生变化带动其周围的液体跟着变化——特别是在气泡体积剧烈变化时,从而导致驱动声场的机械能发生损失,气泡体积变化越剧烈,驱动声场的机械能损失越大;对于驱动声场的传播来说,由于气泡的存在,声场在传播过程中会导致气泡振动,如果声场振幅超过气泡空化的Black域值,就会在声源附近产生一个气泡空化的区域,但由于气泡振动会导致声场的振幅变化,所以气泡空化区域的大小会受到气泡多少及声场强度的影响。如果气泡能够发生空化的话,则气泡越多驱动声场强度越小,这个区域就越小,这一结论与文献 [16] 中根据实验等到的相关结论相似。最终我们认为含气泡液体中声场能量传播模型的提出及应用可以较方便地用来处理声场在含气泡液体中的传播问题。
基金项目
国家自然科学基金资助项目(11874253)渭南职业技术学院科研项目基金(WZYZ201502)。