1. 引言
重卡作为由车架、发动机、变速箱、车桥等组成的工业品，其运营环境相对乘用车及工程车辆更加复杂、恶劣。因此需要在整车开发阶段，进行大量的试验查找出车辆在运行过程中可能出现的问题，同时将每次试验采集数据进行积累，并结合大数据分析方法为后续整车的优化提供参考，国内专家方王永峰等已将基于大数据可靠性的计算应用于悬索桥可靠性的计算 [1]。支架结构(如油箱支架、挡泥板支架)作为整车的重要组成部分，由于在整车行驶中受到来自路面的振动激励，对附属件的耐振动性能提出了更高的要求。在大量的市场反馈中，出现问题较多的是支架类结构，常见的故障模式为振动疲劳断裂。目前除了可以结合整车耐久试验验证支架类结构的耐久性能，还可以通过台架试验或有限元计算的方式达到验证的目的。
振动台架试验虽然能够很好的验证支架类结构的疲劳特性，但振动台架及试验工装存在投资大，试验时间长的问题，有限元分析可以很好的避开台架试验存在的问题，因此用有限元手段取代台架试验成为了研究的主要方向。
台架疲劳试验根据载荷的不同可以分为随机振动、基于PSD的振动、定频振动等 [2] [3] [4]，需要根据实际工况选择合适的方法进行试验。鲍晓东等结合PSD振动疲劳试验与仿真计算方法完成了某商用车尿素箱支架的设计 [5]。杨志刚等将采集的振动数据应用于有限元模型计算，成功解决了某重型汽车后尾灯疲劳断裂的问题 [6]。张志远等借助试验与有限元分析的方法完成了某重型牵引车冲焊后桥结构与铸钢后桥结构的疲劳开裂分析与对比 [7]。刘文华等借助有限元分析方法解决了喇叭支架在振动疲劳中的断裂问题 [8]。
基于先前的研究，对振动疲劳的研究主要集中于随机振动或PSD振动较多，对定频疲劳振动的研究相对较少。本文以某重型牵引车挡泥板支架为研究对象，将台架试验方法与有限元分析方法相结合，对其定频振动疲劳进行了研究，通过试验了验证有限元计算方法的可行性，为后续用有限元方法替代台架试验提供了参考。
2. 试验
2.1. 定频试验
定频试验指在规定的固定频率点上进行各种振动参数不同量级的试验，用于验证产品在共振点或预定危险频率下承受振动的能力。在进行试验前需要通过扫频的方式确定试验件的共振频率点，若验证产品在规定时间、规定的频率下能够完成相应试验，则可判定设计是合理的。
2.2. 台架扫频
为了完成某重型卡车挡泥板支架的定频疲劳试验，特设计了相关的台架，模拟挡泥板支架在实车上的安装状态，在试验中将台架固定在振动台面上，如图1所示。重卡车辆在道路上行驶时的激励主要来自路面，在0~100 km/h的时速范围内，激励频率为0~9 Hz，同时在襄阳国家试验场，路面的激励频率在20 Hz以下(比利时路为18 Hz)。为了获取挡泥板支架的共振频率，在控制系统中设置扫频范围为0~100 Hz，沿垂向在台面上施加0.5 g的载荷，分别完成挡泥板支架两种状态的扫频，即在挡泥板支架上悬挂挡泥板和未悬挂挡泥板。
两种状态的扫频结果如表1所示，未悬挂挡泥板时的一阶共振频率为25.78 Hz，悬挂挡泥板时的一阶共振频率为15 Hz。悬挂挡泥板会降低一阶共振频率点，使其下降了41.8%。
Table 1. Frequency sweep results (Hz)
表1. 扫频结果(Hz)
2.3. 台架耐久试验
根据台架扫频结果，将定频疲劳试验的频率设定为15 Hz，同时在采集的襄阳国家试验场路谱中，挡泥板支架与车架连接端的垂向加速度在2 g~3 g之间变化，同时考虑一定的安全系数，决定在试验中沿垂向施加5 g的载荷。在试验进行至51分钟时出现开裂问题，且裂纹长度已超过圆管周长的一半，开裂状态如图2所示。在试验进行中，不定期的检查挡泥板支架的状态，根据记载试验进行18分钟时，在开裂位置无明显裂纹；试验进行至38分钟时，开裂位置无明显裂纹；试验进行至51分钟时，即振动45900次，出现明显的开裂，试验停止。
Figure 2. The crack shape of fender support
图2. 挡泥板支架开裂状态
3. 有限元分析
为了实现以有限元计算方法替代台架试验的目的，结合台架建立了有限元分析模型，如图3所示，其中两块挡泥皮的质量分别为2.365 kg，4.475 kg，材质为PP，挡泥板支架的材料为Q345。在仿真计算中，结合台架约束车架与工装焊接的位置。在建立的有限元模型基础上完成了有挡泥板和无挡泥板状态的模态计算及悬挂有挡泥板时的频率响应。
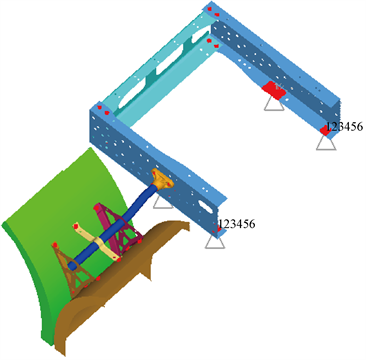
Figure 3. Finite element model of bench simulation
图3. 台架模拟有限元模型
3.1. 无挡泥板时的模态计算
为了验证有限元模型的准确性，首先对未悬挂挡泥板的模型进行了模态计算，前4阶模态结果云图如图4所示，具体结果如表2所示。第1阶模态频率为25.83 Hz，与扫频结果高度吻合，表明搭建的有限元模型是准确的。
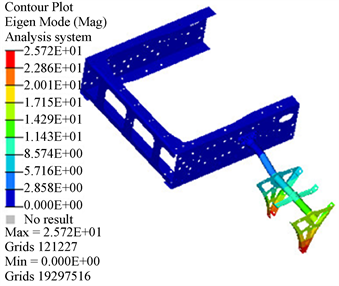(a) 第1阶模态 
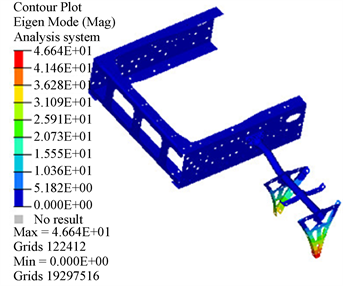(b) 第2阶模态 
(c) 第3阶模态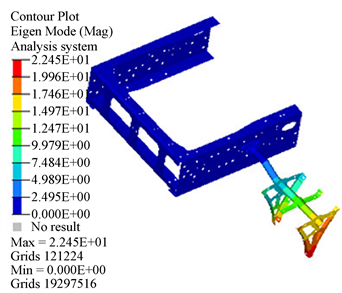 
(d) 第4阶模态
Figure 4. Modal shape of fender support without fender
图4. 未悬挂挡泥板时的挡泥板支架模态振型
Table 2. Results of modal calculation (Hz)
表2. 模态计算结果(Hz)
3.2. 有挡泥板时的模态计算
在挡泥板支架定频疲劳试验中安装有挡泥板，为了验证扫频结果的准确性，对悬挂有挡泥板的模型进行了模态计算，第5到第8阶模态如图5所示，具体结果见表3。在呈现的4阶模态中，只有第7阶模态表现为挡泥板支架的振动，其余三阶模态表现为挡泥皮的局部模态，此时挡泥板支架的频率为16.0 Hz，台架扫频结果为15 Hz，误差为6.6%，误差在可接受的范围内，表明有限元模型建立的方法是准确的，为后续的频响计算及疲劳计算提供了有利的支持。
3.3. 悬挂有挡泥板模型的频响计算
在疲劳计算中，首先需要完成模型的频响计算，获取模型在不同频率下应力与频率的响应关系。为了完成后续的疲劳计算，基于上述悬挂有挡泥板的有限元模型，在约束位置沿Z向施加1 g (g为重力加速度)的单位载荷，并基于模态法完成了10~30 Hz的频响计算。由于挡泥板是一个柔性体，其阻尼对计算结果存在很大的影响。因此，在计算中对施加不同阻尼的频响结果进行了对比，在挡泥板支架上，应力相对较大的位置位于试验开裂位置。开裂位置节点137751的应力在不同阻尼下随频率的变化曲线如图6所示，应力峰值出现在16 Hz，具体的应力值如表4所示，应力随着阻尼的增大逐渐的变小，应力所在的频率与试验频率(15 Hz)基本一致。
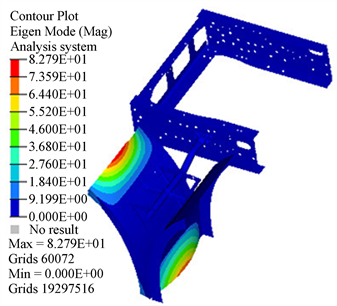(a) 第5阶模态 
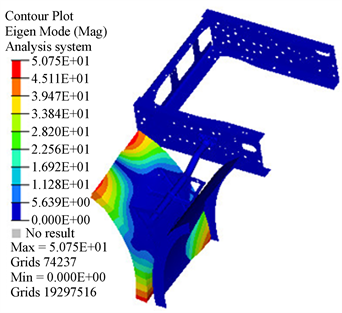(b) 第6阶模态 
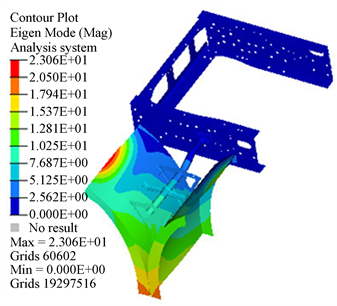(c) 第7阶模态 
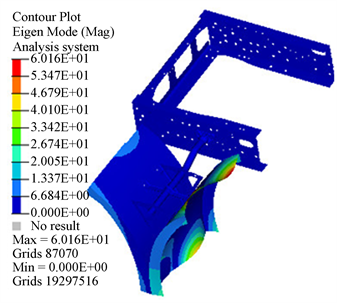(d) 第8阶模态
Figure 5. Modal shape of fender support with fender
图5. 有挡泥板时的挡泥板支架模态振型
Table 3. Results of modal calculation (Hz)
表3. 模态计算结果(Hz)
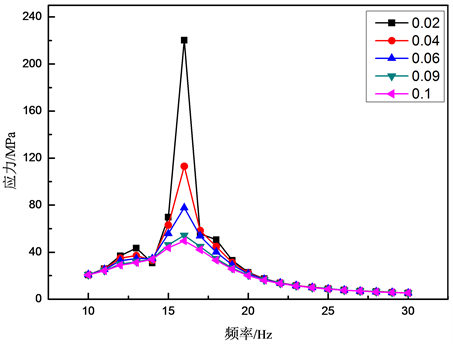
Figure 6. Stress response curve of node 137751 changing with frequency
图6. 节点137751随频率变化的应力响应曲线
Table 4. Peak stress of node 137751 at different damping (MPa)
表4. 不同阻尼下节点137751的峰值应力(MPa)
3.4. 疲劳计算结果
在nCode中搭建了疲劳分析流程，如图7所示，用于疲劳计算的载荷通过Vibration Generator产生，通过输入幅值、频率、循环次数，产生疲劳计算载荷，在计算中，根据频响计算结果以及试验载荷确定了如表5所示的疲劳计算载荷。
S-N曲线是疲劳计算的关键，在nCode中根据挡泥板支架材料Q345的材料参数(弹性模量、抗拉强度)自动生成计算需要的S-N曲线。根据挡泥板支架寿命计算结果，在试验开裂位置的寿命是最低的，图8为在不同阻尼下疲劳计算结果，代表着在振动这样的次数后，可能会有裂纹的萌生。在0.02、0.04、0.06
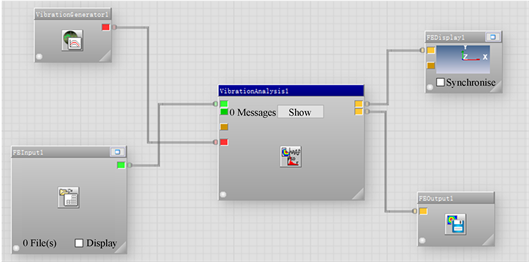
Figure 7. Fatigue calculation process of nCode
图7. nCode疲劳计算流程
Table 5. The load of fatigue calculation
表5. 疲劳计算的载荷
注：循环次数设为1，表示以频率为16 Hz、幅值为5 g的正弦函数作用一次。
三种阻尼下，挡泥板支架的寿命较短，甚至出现寿命为0的情况，与实际情况相差较大。在0.09、0.1两种阻尼下，寿命结果与实际比较均能够满足需求，但考虑到损伤是一个持续累积的过程，在阻尼0.1时其寿命与实际断裂时的振动次数比较接近，计算时取阻尼为0.09比较合适。在阻尼为0.09时，开裂位置的寿命为16,409 (17.09 s)，即17.09 s分钟有裂纹的产生。根据疲劳理论，金属疲劳破坏分为三个阶段，即裂纹萌生、裂纹扩展、失稳断裂 [9]，前两个阶段占据疲劳断裂的大部分时间。结合试验结果试验进行51分钟时，挡泥板支架已经出现很长的裂纹，在远小于试验时间的情况下，已经有了裂纹的产生。表明仿真结果与试验结果是比较一致的，为后续用有限元方法预判结构的开裂位置及失效时间提供了依据。
4. 结论
为了实现用有限元计算方法替代试验方法预判结构失效位置及失效时间的目的，对某重型卡车挡泥板支架进行了研究，将台架试验与有限元计算结合起来，通过结果对比得出以下结论：
1) 台架扫频结果与模型模态分析结果高度吻合，表明有限元模型建立的方法是准确的；
2) 频响计算结果应力峰值出现的频率与定频疲劳试验的频率误差为6.6%，误差较小，也验证了模型建立的准确性；
3) 在不同阻尼下，频响应力峰值随着阻尼的增大逐渐减小；
4) 将不同阻尼下的疲劳寿命与试验结果进行了对比，并结合理论，认为在频响计算中将结构阻尼确定为0.09是与实际情况比较相符的；
5) 通过以上的分析，可以得出用有限元计算方法评估结构在某一频率下的疲劳寿命是可行的。