1. 引言
相比于NURBS (非均匀有理B样条)建模,细分曲面建模的数值更为稳定,更易实现,并且适用于任意拓扑结构。细分曲面的基本思想是对初始多边形网格重复细化,最终拟合为光滑曲面。细分曲面的概念简单,不需要对算法做重大改变,便很容易被修改 [1]。细分曲面广泛地应用在声学、电磁学、计算机制图、3D打印、动画和游戏等领域。
边界元法的实质是只对定义域的边界离散,而不需要对域内离散,具有计算精度高和数据准备简单的优点 [2]。用边界元法求解非线性问题时,会遇到同非线性项所对应的区域积分,这种积分在奇异点周围有强烈的奇异性,因而求解过程存在困难 [3]。
将细分曲面和边界元法结合,能根据不同精度对细分层级网格的要求做相应的调整,省去前处理中模型的重复离散过程。本文介绍了基于Catmull-Clark的细分曲面方法和基于Catmull-Clark的声学边界元法的详细计算过程,此外,通过分析散射球模型在平面波入射的声散射响应,以及散射球内某点的散射声压分布情况,证明CCBEM算法的有效性和正确性。本文创新性地将CBIE (传统单边界积分方程)和组合Burton-Miller边界积分方程应用于散射球模型的数值计算中,并比较两种方法在数值计算中的优缺点,发现基于CBIE的数值结果在某些频率上偏离解析解,但基于组合Burton-Miller边界积分方程的结果和解析解几乎一致。
2. 基于Catmull-Clark的细分曲面方法
2.1. Catmull-Clark细分规则
CC (Catmull-Clark)是将任意四边形网格细分为四个子四边形网格的算法 [4]。k级网格细分一次生成三种顶点:1、原始网格根据周围顶点权重获得顶点V;2、在任意四边形单元的各边的中部插入E顶点;3、在任意四边形单元的中心位置插入F顶点。三顶点的计算表达式如下 [5] :(如图1所示)
1)
顶点坐标为:
(1)
,
,
,
和
为相邻顶点坐标。
2)
顶点坐标为:
(2)
,
,
,
,
,
为相邻顶点的坐标。
3)
顶点坐标为:
(3)
,
,
,
为四边形单元的坐标。
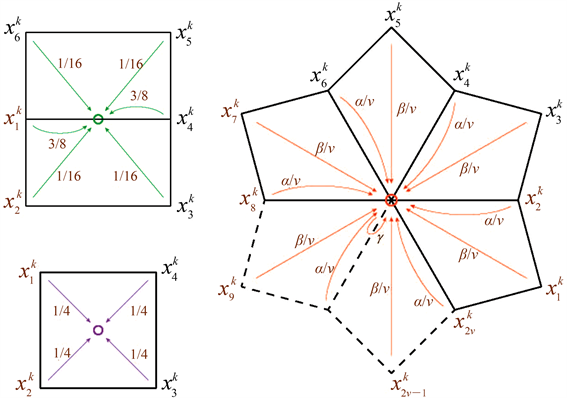
Figure 1. Distribution of edge point “E”, midpoint “F” and vertex point “V”
图1. 边点E和顶点V的分布
2.2. 曲面拟合
2.2.1. 规则单元曲面拟合
规则四边形单元曲面拟合时,拟合单元内某点的局部参数坐标为
。该点的笛卡尔坐标
为 [6] :
(4)
为第i个相邻顶点的坐标,参数域满足
,
为双三次B样条基函数
(5)
为余数,
为除法,N为三次B样条基函数
(6)
(7)
(8)
(9)
2.2.2. 不规则单元的曲面拟合
对于不规则单元的曲面拟合,拟合点坐标为 [7] :
(10)
为拾取矩阵,
为初始拟合点x的坐标,
为细分后规则子单元中拟合点x的坐标。
规则单元中,拟合点的笛卡尔坐标
为
(11)
是第i个相邻顶点的坐标,
是不规则单元的基函数,
是基函数矩阵
(12)
3. 基于Catmull-Clark的声学边界元法
3.1. 声学边界积分公式
控制声域的赫姆霍兹方程为
(13)
为拉普拉斯算子,
为点x处的声压,波数为
,
为角频率,c为传播流体域中的声波速度。对公式(13)进行一系列转换后,可以得到以下边界积分方程
(14)
为入射波声压,
和v为边界积分算子。
对公式(14)求法向导数积分方程,可得积分方程 [8] :
(15)
在外边界值问题中,公式(14)和(15)单独使用时,方程式存在虚拟特征频率。但是,这两个方程的线性组合可以克服该问题,对于如何克服虚拟特征频率的详细过程,可参考 [9] 表示如下
(16)
为组合参数:当
时,
,否则
。
3.2. 离散化
首先,用CC细分单元离散边界,再用物理场近似每个单元,
(17)
、
为
单元内点
的声压、法线通量,
、
为
单元网格中某节点的声压、法线通量。
(18)
通过使方程式(18)保持在选定的搭配点上,并集合这些公式,可以得到以下等式,
(19)
H、G是CCBEM的系数矩阵,p、
是配置点处的声压和入射波矩阵。
4. 数值例子
散射球
对于具有解析解的半径为5的散射球,本文给出初始粗糙离散四边形模型,然后对其连续细分操作,以观察每个细分层次,如图2所示。从图2可知,散射球模型中存在的不规则点,不会随细分次数的增加而变化,规则点随细分次数,成指数形式增长。
构建光滑球形模型后,本文分析了极限球形模型在平面波入射时的声散射响应,以证明CCBEM方法的正确性。平面波沿X轴正向传播,幅度为1。本文研究了点
处频率的散射声压,如图3所示。CBIE和组合Burton-Miller边界积分方程用于数值计算。由图4可知,基于CBIE方程的数值结果在某些频率上偏离解析解,但是基于组合方程的结果和解析解几乎一致。这是BEM(边界元法)方法在解决外部声学问题时的一个特殊问题,但不是分析模型时存在的固有问题。若模型在某频率上无法得到正确结果,则该频率称为虚拟特征频率。此外,图4还验证了在本文中得以发展的CCBEM算法的正确性。
如图3所示,相同的极限光滑模型用于多频响应分析。从图4可知CBIE的结果在几个虚拟频率上迅速振荡。随着频率越来越高,模型中虚拟频率的分布越来越密集。但是,组合方程的结果在整个频率带上都非常平缓。
 (a) 实部
(a) 实部 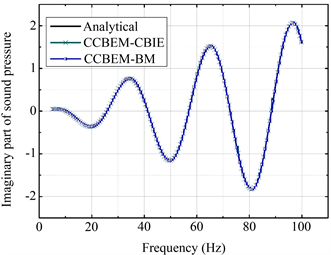 (b) 虚部
(b) 虚部
Figure 3. Comparisons between numerical and analytical solutions of sound pressure at a point of (10;0;0): (a) Real part of sound pressure as a function of frequency; (b) Imaginary part of sound pressure as a function of frequency. The frequency step is 0.1 Hz
图3. 点(10;0;0)处声压的数值解和解析解两者之间的比较:(a) 声压随频率变化的实部;(b) 声压随频率变化的虚部。频率步距为0.1 Hz
 (a) CBIE的声压
(a) CBIE的声压 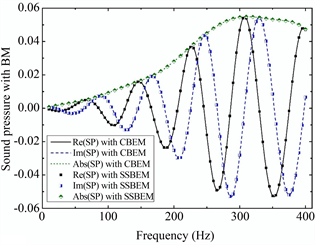 (b) BM的声压
(b) BM的声压
Figure 4. Changes in the real, imaginary, and amplitude of the sound pressure at point (2; 0; 0) with frequency: (a) CBIE is used for numerial solution; (b) BM is used for numerial solution. Black solid line denotes the real part of sound pressure with CBEM; Dash line denotes the imaginary part of sound pressure with CBEM; Dot line denotes the amplitute of sound pressure with CBEM; Three different types of scatters are used to represent the solution by CCBEM
图4. 点(2;0;0)处的声压的实部,虚部和幅度随频率的变化情况:(a)CBIE用于数值解;(b)BM用于数值解。黑色实线代表CBEM(传统边界元法)的声压的实部;虚线代表CBEM的声压的虚部;CCBEM使用三种不同类型的散射来表示解决方案
对于虚拟频率的分布情况,可由以下计算过程得知:
在Neumann边值条件下:
若边界径向速度给定为
,则系数A满足 [10]
(20)
可得
(21)
则对应内域声场问题的特解为
(22)
由上式可知,Neumann边值条件的内域声场问题的特征波数为使
的k值,即满足
。由上述计算过程可知,对于脉动球算例,常规边界积分方程的非唯一解出现在
处。
图5显示了两个频率上,极限光滑球形曲面上的声压的实部、虚部,以及曲面误差的分布。并且,从图5可知,图形具有良好的轴对称性。极限球两端的误差很小,但中部的误差很大。另外,频率越大,极限球面上的误差越大。
5. 总结
本文用基于CC的细分曲面法和基于CC的声学边界元法,研究了散射球在平面波入射时的声散射响应,从而验证了CCBEM的正确性和有效性,并发现球模型中存在的不规则点,不会随细分次数的改变而改变,基于CBIE方程的数值结果在某些频率上偏离解析解,但基于组合Burton-Miller边界积分方程的计算结果和解析解几乎一致。