1. 引言
储层预测是储层评价研究中的重要的问题,但由于岩心的取芯和测试费用较高,岩心测量数据一般较少且不连续。测井解释研究工作之一就是结合已有岩心数据与测井数据来求取全井段的地质属性。一般来说,生产单位目前用的测井模型为一元线性回归模型 [1],例如对储层孔隙度的预测,即在四性分析的基础上选择与孔隙度相关性最好的一种测井参数来建立模型,这种模型能够简单快捷地对储层孔隙度进行预测,但预测精度不高且无法应用于非均质性较强的地层。本文所用的储层分类预测方法,不用对储层的孔隙度和渗透率具体值进行预测,而是在对样本进行储层分类的基础上,利用预测模型,直接对未知储层进行分类预测,求得有效储层,从而跳过对储层孔隙度以及渗透率具体值预测的基础上再根据预测值进行分类的繁琐步骤。
为了应对如致密砂岩储层这种非均质性较强的地层,目前测井解释模型已经运用了多种非线性方法,如偏最小二乘法 [2] 、逐步回归法 [3] 、核岭回归法 [4] 、人工神经网络法 [5] 等。相比于人工神经网络对样本的需求量较大 [6],支持向量机(SVM)模型以其对样品数量需求小,可解决高纬度非线性问题以及可避免神经网络模型易陷入局部极小值的特点逐渐进入人们的视野 [7]。支持向量机是Corinn Cortes与Vapnik [8] 在90年代首次提出的一种基于统计学习理论和结构风险最小化原理的机器学习方法,它的主要特点是能够深度挖掘数据之间的关系并在模型的复杂性和模型的学习能力之间寻求最佳折中。近几年来,许多研究者在支持向量机对于储层的孔隙度预测方面取得了较大的研究成果。乐友喜等 [9] 利用支持向量机方法对胜利油田某区块进行砂体孔隙度预测并与人工神经网络方法进行对比,证明了人工神经网络与支持向量机相比在样本较少时会出现欠学习现象而使预测结果不理想。滕新保 [10] 等将岩性信息加入支持向量机模型,并证明了径向基函数(RBF)对支持向量回归模型最好。
一般而言,人们在对储层孔隙度运用支持向量机方法进行预测时,通常使用网格搜索法来寻找适合模型的最优化参数c和
,这种穷举搜索方法往往需要人们在准确度和消耗时间之间作出妥协,做不到既准确又迅速。张向君等 [11] 通过交互检验方法优选支持向量机的惩罚因子及核函数参数,提高支持向量机储层预测精度。李建军等 [12] 通过拐点法的数值实验选择出高斯函数。然后针对石油地质勘探的实际问题,将支持向量机运用测井曲线预测储层参数。本文则提出利用粒子群寻优的方法,不必地毯式搜索也可以快速、准确地找到适合模型的最优参数。
位于珠江口盆地的珠一坳陷,其古近系从深到浅依次为文昌组、恩平组、珠海组,其中的文昌组和恩平组储层非常发育,以致密砂岩储层为主。在文昌组沉积时期,盆地主要为断陷湖泊沉积环境,从而形成了中深湖–浅湖–辫状三角洲沉积体系;而在恩平组时期,盆地处于断拗转换阶段,主要形成滨浅湖–河流、三角洲–沼泽沉积体系 [13]。储层岩石结构主要以中砂岩和粗砂岩为主,孔隙度分布在7%~20%,渗透率分布在0.02~1000 mD,层间的非均质性较强。由于每口井之间测井年代不同,所用测井仪器不同,测井曲线也有一定的缺失,所以本文在测井曲线标准化的基础上,采用针对地区典型井分层位的方法建立测井预测模型。此种方法建立的预测模型具有较强的针对性,而且改进后的支持向量回归算法也能解决模型细分后样本数量减少的问题。
2. 原理分析
2.1. 支持向量分类原理
支持向量机分类原理与支持向量回归原理相似,即是将低纬空间中的数据映射到高纬空间中,并在高纬空间中寻找一个回归超平面,使所有数据到该超平面的距离最近。对于已知数集
(1)
在任意给定数
情况下,存在超平面
(2)
使得所有数据到该超平面的距离最近。其中,
为惩罚程度,
为权重向量,
为权重向量
与向量
的内积,
为偏置系数,基于结构风险最小化原则,引入松弛变量
,分别代表上下边界的松弛因子,即可得到支持向量机公式 [14],它要解决的原始最优化问题为
(3)
(4)
式(3)中常数
为惩罚系数。通过引入拉格朗日乘子
,并根据带有不等式约束的极值问题的KKT条件,将原始最优化问题转化为其对偶问题 [15]
(5)
通过引入核函数
来代替对偶问题函数式(5)中的内积
,可将低维空间中非线性不可分样本映射到高维空间中,使其线性可分。求解对偶问题即可得到
(6)
其中的实验涉及的致密砂岩是具有较强非均质性的储层,故核函数使用非线性效果较好的径向基函数 [5],公式为
(7)
式(7)中的
为核宽度系数,用于控制高维度空间中样本分布的复杂程度。将核函数代入,即可得到本次实验所用支持向量机模型 [16] 公式
(8)
2.2. 粒子群寻优原理
支持向量回归模型中的参数c和
对模型影响较大且难以寻得最优值,本文选用粒子群寻优原理,寻找模型参数c和
的全局最优解,并以交叉验证的模型的评估分数来判断模型的优劣。
粒子群寻优算法(PSO)是一种群体智能优化算法,它通过在空间中模拟鸟群觅食行为寻找最优值。假设在一个N维的空间中,共有n个粒子
,每个粒子代表问题的一个潜在解。通过不断地迭代,粒子根据个体之间的相互作用及信息共享寻找最优值。设第i个粒子的速度为
,其个体极值为
,种群的历史最优值为
。每次迭代中,粒子速度和位置更新公式 [17] 如式(9)、式(10)所示:
(9)
(10)
式(11)中的
表示第i个粒子的第k次迭代状态量,
,
和
为[0,1]之间的随机数,用于保持群体的多样性,适当调整学习因子
和
,扩大搜索空间避免陷入局部极值。
3. 改进支持向量回归预测模型
3.1. 数据标准化
由于多条测井曲线的刻度和量纲均有所不同,所以在进行储层类型预测建模时,必须要对所有参与建模的测井曲线进行数据标准化处理,来消除由于量纲和刻度不同造成的大量刚数据在模型中占比过大等影响。为了消除E2井的井径扩大段出现的异常最值等离群数据的影响,本次标准化采用的是z-score标准化,其公式如式(11)所示:
(11)
式(11)中的
为实际测井曲线上对应的测井深度的测井值,
为
的标准化后的值,
为E2井恩平组所有采样点测井曲线的算术平均值, 为对应的测井曲线标准差。本文通过Python3.6软件编程实现对GR、DT、DEN、CNL、RT等测井曲线的批量标准化。
3.2. 样本分类与选择
3.2.1. 储层下限分类
为了保证建模样本的多样性,避免出现模型偏向低孔隙度或高孔隙度,本文采用有利储层下限,对样本进行分类,再从各分类中进行选取的方法来保证样本的多样性。本文主要采用了典型井测试与试采分析法,选择具有取心资料的测试或者累产低产、中产、高产层进行物性分析,分别确定出这些典型层位的物性特征,在此基础上求取了各类产层的孔隙度和渗透率均值,这些典型层位的物性均值即为物性下限。根据上述方法中确定的储集物性下限,可将E地区恩平组储层按照储集物性的好坏依次分为I、II、III、IV四类储层,各类储层的孔隙度和渗透率如表1所示。

Table 1. Reservoir classification and evaluation of Enping formation in Zhu I depression
表1. 珠一坳陷恩平组储层分类评价表
其中I类为在自然开采条件下能够获得较好产能的储层;II类为自然开采条件下基本能够获得工业产能的储层;III类储层在自然开采条件下不能达到工业产能,但稍加改造后就能够产出油气;IV类储层为含油性很差的储层或是非储层。
3.2.2. 样本选取
将珠一坳陷27口重点井恩平组的204个实测岩心样本依据照表1分为四类。其中III类储层样本数最少,只有7个,随机选取其中的80%作为模型样本,即5个Ⅰ类储层样本。依次再在另三类储层每种类型随机挑选80%的样本,剩下样本作为训练样本,模型样本与训练样本的分配如表2所示。

Table 2. Sample distribution of Enping formation in well E2
表2. E2井恩平组样本分配表
3.3. 模型建立
本文采用27口重点井恩平组的204个实测岩心样本中挑选出的163个实测岩心样本,剩下41个实测样本作为测试样本进行交叉验证。所有样本数据根据测井响应识别的原则,选取代表地层特征的5个参数,其中GR为伽马,RD为深侧向电阻率,DT为声波,DEN为体积密度,CNL为中子密度。
为了应对目标储层非均质性较强的特点,本文选用支持向量机的非线性核——径向基函数,作模型的核函数,其中支持向量机的惩罚系数c和径向基函数参数
由粒子群寻优法来求最优解。粒子群寻优设置粒子为30个,以惩罚系数c作为横坐标,径向基函数参数
作为纵坐标,初始位置为c和
都在0.1~10之间的一个随机数,由于c和
的有效范围在
之间,所以为了减少粒子的盲目探索,初期粒子的每次移动乘以10作为一个步长,当确定大致范围后再缩小每次移动的步长。本次建模使用Python3.6.3编写模型处理程序,模型建立流程如图1所示。
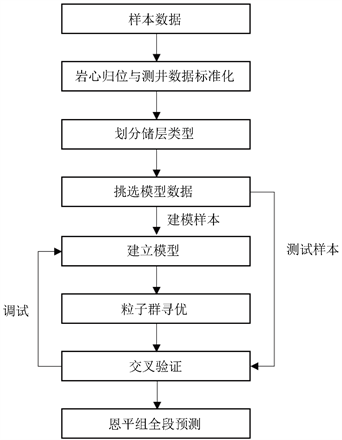
Figure 1. Establishment process of Enping prediction model
图1. 恩平组预测模型建立流程
在岩心归位与测井曲线标准化的基础上,对归位后的岩心依据物性数据进行储层分类,然后对每种类型的储层选取其中80%的数据进行建模,运用粒子群寻优算法求得支持向量机的模型参数参数c和
,并用根据交叉验证分数实时调试粒子群,最终寻得模型最优参数c和
并建立模型。将剩下的20%岩心数据用于检验模型的预测正确率,若模型的总体预测正确率大于80%即可说明模型达到精度要求,最后将达到精度要求的模型用于恩平组全段的储层预测。
3.4. 预测结果及分析
对模型参数c和
的粒子群寻优过程如图2所示,图中的横坐标为粒子群寻优迭代次数,本文设定的最大迭代次数为200次,图中的纵坐标为目前为止寻得的最佳参数在交叉验证时的模型评估分数(cross_value_score),其值越接近1,则模型准确度越高。整个寻优过程在迭代到151次时达到最优值0.8695,用时4209秒,寻得的c = 5.107053011237296,
= 3.2348451984267936。
本文同时也使用了常用的网格搜索法进行寻优并与粒子群寻优进行对比。由于网格搜索法原理为使用穷举法来将所用的参数都运行一遍,如果采用和粒子群寻优相同精度,运算量就过于庞大,所以本文使用的网格搜索法在编程时设定的步进间隔大小为1。但即便如此,运算时长依然超过了4小时以上。得到的模型评估分数最优值为0.8633,寻得的c = 5.110,
= 3.235。与网格搜索法相比,虽然两种模型差距较小,粒子群寻优需要人为输入的参数更少,寻优过程全部由程序完成,且粒子群寻优算法的收敛速度较快。
经过对模型的优化,再将得到的模型用于对未参与建模、也未参与检验的E2井恩平组85个实测岩心样本进行预测,得到的预测储层分类结果与实测储层分类结果对比图如图3所示,从图中可以看到两幅图的孔隙度和渗透率均为岩心实测值,其中绿色样本点为IV类储层,蓝色样本点为III类储层,红色样本点为II类储层,黄色样本点为I类储层。85个实测样本中各类储层预测的正确率如表3所示。

Figure 2. Process chart of particle swarm optimization
图2. 粒子群寻优过程图
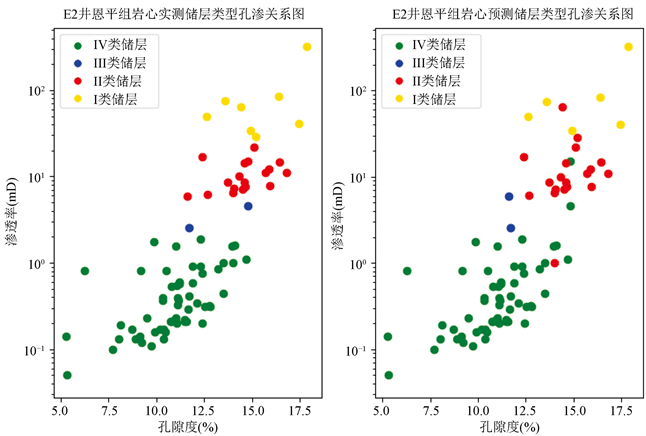
Figure 3. Comparison of the relationship between the measured core and the predicted reservoir type porosity and permeability in Enping formation of well E2
图3. E2井恩平组岩心实测与预测储层类型孔渗关系对比图

Table 3. Statistical table for prediction accuracy of reservoir type of measured samples in well E2
表3. E2井实测样本储层类型预测正确率统计表
由表3可以看出,尽管模型的精度较高,但模型对于Ⅲ类储层高孔隙度依然不太敏感,预测精度较低,模型出现了精确度有偏差的情况。对于此种情况,可能是由于建模的时候Ⅲ类储层的建模样本数较少的原因造成。
将建立好的预测模型对E2井恩平组全段砂岩进行储层预测,并在Resform软件中成图,可以得到储层类型的测井解释图如图4所示。

Figure 4. Reservoir type prediction map of Enping formation in well E2
图4. E2井恩平组储层类型预测图
图4中的I类储层由长度为4的黄色线段组成,II类储层由长度为3的橙色线段组成,III类储层由长度为2的蓝色线段组成,IV类储层由长度为1的绿色线段组成。此种预测方法以及显示方式,可以较为精确的看到优质储层所在井段以及精准计算出优质储层的厚度。
4. 结论
1) 粒子群寻优的收敛速度快,与传统网格搜索法相比,具有速度快、准确率高的特点 [18]。将其运用到对支持向量机回归模型的参数c和
的寻优中,可以得到相对误差较低,精确度较高的预测模型。
2) 根据储层下限对实测样本进行分类,可以在建立预测模型时确保建模样本的多样性。在检验模型时,对测试样本正确率进行分类统计,可以看出模型对于每类储层的预测精确度,对模型精确度不高的储层可以适量增加该类储层在建模样本中所占的比例。
3) 将模型运用于检验井恩平组全段砂岩的储层类型预测,可以较为准确的得到优质储层所在位置及优质储层的厚度。