1. 引言
2013年以来,塑料瓶装水禁令在美国的许多地方被通过并执行,其中包括马塞诸塞州的康科德镇,加州的旧金山和其他一些西方国家的城市。根据政府颁布的相关法令,体积小于1升的塑料瓶装饮用水的售卖被禁止,但其他饮料和更大包装饮用水的售卖不受限制。禁令的支持者认为日益增长的塑料制品需求给地球带来了严重的危害,塑料瓶装水不仅对水源地的环境有负面影响,在生产中也消耗大量的能量及资源,同时还产生大量不可降解废料,造成多种环境污染问题。但禁令的反对者认为,在危机情况下,比如地震、飓风时,人们无法通过其他方式获取可饮用的水,塑料瓶装水相当地重要;他们还对此禁令在相关工业中可能造成的失业问题表示担忧。
关于禁令的争辩一直在持续,本文试图通过建立数学模型对塑料瓶装水禁令所带来的经济和环境等影响给出定量评估,从而为决策者提供一定的参考。首先,我们通过政府网站,企业、行业协会等网站收集环境、经济有关的数据,利用时间序列图选取对禁令敏感的指标,即禁令前后发生显著性改变的指标,采用分段线性稳健回归 [1],建立了禁令对单指标的影响力模型,最后利用层次分析综合评级方法 [2] 给出禁令综合影响力的定量分析。
2. 塑料瓶装水禁令对单指标的影响力模型
2.1. 分段线性回归模型引入
2013年是美国瓶装水禁令的关键时间点。我们认为该禁令对经济,环境均有影响。如塑料瓶装水的放弃PET作为塑料瓶装水的材料。为此,我们认为,塑料瓶装水的销售将直接受到该禁令影响,进而影响公司的营业和产品。我们进一步认为,瓶装水销量的增速会放缓,这会导致公司量和PET公司的收入来衡量禁令的影响。而塑料瓶装水销量减少也可能造成塑料类垃圾的减少。
由于该禁令是突发性的,在2013年前后各个指标都有着截然不同的变化趋势。通过进一步观察和分析,我们发现PET塑料瓶垃圾体积、PET塑料厂家的收入、其他饮料的市场占有率、行业失业率等在2013年前均服从一种线性关系;由于受到塑料瓶禁令的影响,2013年后服从另一种线性关系。因此,我们考虑建立由两段构成的分段线性回归模型。
为了拟合分段线性回归模型,常见方法是用最小二乘估计方法。最小二乘估计一般受异常点的影响较大。考虑到我们收集数据的样本量较少,并且为了减小异常值的影响,我们通过稳健回归方法来给出分段线性回归方程的系数估计。
为了考察塑料瓶禁令对指标的影响,我们用禁令前后指标斜率的相对变化率来作为禁令影响力度量。相对变化率与绝对变化相比不受量纲的影响,这是我们选取相对变化率的主要原因。
2.2. 分段线性稳健回归模型与求解
假设y为指标因变量,时间t为自变量。在点
处的虚拟变量定义为
(1)
分段线性回归模型为
(2)
其中
为随机误差项,满足
。由模型我们可得
的数学期望为
(3)
假设我们收集到数据样本为
。考虑到我们收集数据的样本量较少,并且为了减小异常值的影响,我们通过稳健回归方法来给出分段线性回归方程的系数估计。
首先我们定义绝对误差和为
(4)
那么
的估计
满足
(5)
该估计称为稳健回归估计。
由于l是一个含有绝对值的非线性目标函数,很难进行优化求解,我们可以转化为线性规划问题或者通过引入Huber损失函数转化为具有光滑性的目标函数进行求解等,这里就不再给出。我们利用R软件包MASS的函数rlm()给出的
的稳健回归估计。
2.3. 塑料瓶装水禁令对单指标影响力的度量
假设y为一环境、经济指标,该指标为时间t的函数,
为禁令颁布的时间。由于塑料瓶禁瓶令的影响,在时刻
后函数发生了变化,假设变化后仍为线形函数,即
为分段线形函数,即
满足
(6)
在时刻
后T时间内塑料瓶禁令对该指标的影响力定义为
(7)
的分子
表示在时刻
后T时间内由塑料瓶禁令的影响指标值增加量之和,分母表示在时刻
后T时间内不受塑料瓶禁令的影响指标值之和,因此
表示在时刻
后T时间内由于塑料瓶禁令影响相对变化的量。如果
,则
表示在时刻
后T时间内由于塑料瓶禁令影响相对增加的比例;如果
,则
表示在时刻
后T时间内由于塑料瓶禁令影响相对减少的比例。
命题:若
,则
证明:
(8)
因此
。
根据上面命题,我们定义塑料瓶装水禁令对该指标的长期影响力为
如果
,则I表示从长期来看,由于禁令影响相对增加的比例;如果
,则I表示从长期来看,由于禁令影响相对降低的比例。
3. 塑料瓶装水禁令对美国环境、经济等影响力的度量
本文收集了美国近年来PET塑料瓶装水垃圾总量、就业率、PET公司的收入、可口可乐市场占有率等相关指标数据,下面我们给出禁令对这些环境、经济等指标的影响力度量。
3.1. 塑料瓶装水禁令对PET塑料瓶装水垃圾量的影响力度量
通过查阅相关文献,我们获得了2007~2017年美国PET塑料瓶装水垃圾总量,见表1。

Table 1. Total waste amount of pet plastic bottled water in the United States, 2007~2017 (Unit: m3)
表1. 2007~2017年美国PET塑料瓶装水垃圾总量(单位:立方米)
为了便于描述,我们令2007年为第1年,2008年为2年,以此类推,2017年为第11年,其中禁令颁布年2013年为第7年。我们以2007~2017年PET瓶装水所产生的塑料垃圾量为解释变量,
为分段点,建立分段线性回归模型。利用R软件的MASS包函数rlm()得出稳健回归方程如下:
图1为2007~2017年PET瓶装水所产生塑料垃圾量的分段线性稳健回归拟合曲线图。
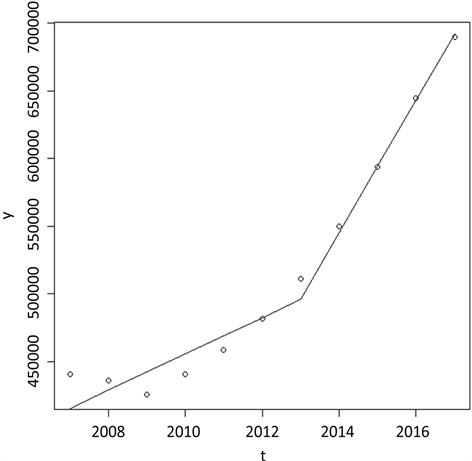
Figure 1. Piecewise linear robust regression fitting curve of total waste amount of pet plastic bottled water, 2007~2017
图1. 2007~2017年PET瓶装水所产生塑料垃圾量的分段线性稳健回归拟合曲线图
由分段线性稳健回归方程可知,在2013年实施禁令前,平均每年的PET塑料瓶垃圾产生量为13,406立方米。2013年后,平均每年的PET塑料瓶垃圾产生量为49,077立方米。由此可见,在禁令发布后,PET塑料瓶垃圾的总量大幅度增加。这可能是由瓶装水的销售总体积增加所导致的,由于一个人对水的日需求基本不变,禁止小瓶PET瓶装水的售卖,导致人们购买大瓶瓶装水,使PET塑料瓶垃圾的总量增加。
根据分段线性稳健回归方程可得,禁令实施后4年来对塑料垃圾袋量的影响力为
即禁令实施后4年来垃圾总量增加了14%。禁令实施后对塑料垃圾量长期影响力为
即从长期来看,禁令实施后塑料垃圾量增加3.66倍。
3.2. 塑料瓶装水禁令对就业率的影响力度量
通过查阅相关文献,我们收集了2010~2019年美国就业率的数据,见表2。

Table 2. Rate of employment in the United States, 2010~2019
表2. 2010~2019年美国的就业率
我们令2010年为第1年,则2011年为2年,以此类推,2019年为第10年,其中禁令颁布年2013年为第4年。以2010~2019年美国就业率为解释变量,
为分段点,建立分段线性回归模型,得到稳健回归方程如下:
图2为2010~2019年美国就业率的分段线性稳健回归拟合曲线图。
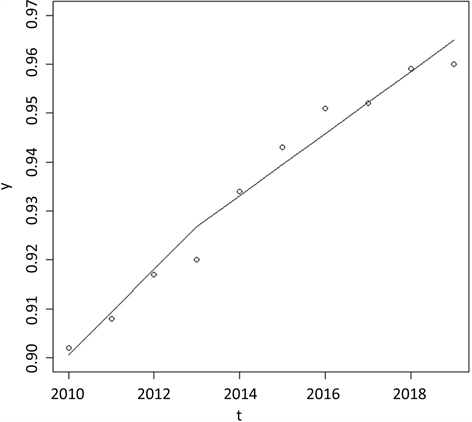
Figure 2. Piecewise linear robust regression fitting curve of the rate of employment in the United States, 2010~2019
图2. 2010~2019年美国就业率的分段线性稳健回归拟合曲线图
由分段线性稳健回归方程可知,在2013年实施禁令前美国平均每年的就业率增长0.87%,在2013年后平均每年的就业率增长0.63%。由此可见,在禁令发布后美国的就业率下降了。这一结果可能是是由于禁令导致的PET行业衰败,导致就业率下降。
根据分段线性稳健回归方程可得,禁令实施后近7年对就业率的影响力为
即实施禁令后近7年来就业率下降了0.76%。禁令实施后对就业率的长期影响力为
即从长期来看,禁令实施使得就业率下降27.59%。
3.3. 塑料瓶禁令对PET公司收入影响力度量
Lyondell Basell是一家PET塑料公司,我们收集了公司的2009~2018年收入的数据,见表3。

Table 3. Annual income of the Lyondell Baselld, 2009~2018 (Unit: Million USD)
表3. Lyondell Baselld的2009~2018年收入(单位:百万美元)
我们令2009年为第1年,则2010年为2年,依此类推,2018年为第10年,其中禁令颁布年2013年为第5年。以2009~2019年美国就业率为解释变量,
为分段点,建立分段线性回归模型,得到稳健回归方程如下:
图3为2009~2018年Lyondell Basell公司总利润的分段线性稳健回归拟合曲线图。
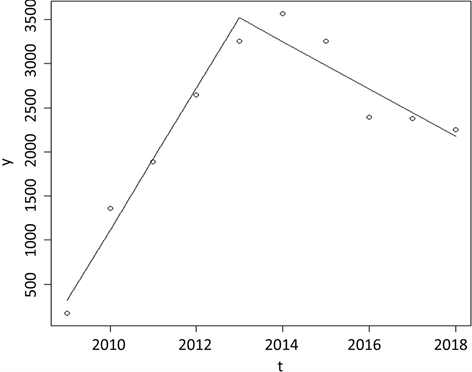
Figure 3. Piecewise linear robust regression fitting curve of the gross profit of Lyondell Basell
图3. Lyondell Basell公司总利润的分段线性稳健回归拟合曲线图
由分段线性稳健回归方程,在2013年实施禁令前,Lyondell Basell公司平均每年的收入增长468.2百万美元。在2013年后,平均每年的收入增长201.6百万美元。由此可见,在禁令发布后,Lyondell Basell公司收入增长降低了。这可能是由于禁令导致的PET行业衰败,导致PET公司利润下降。
根据分段线性稳健回归方程可得,禁令实施后近5年来对Lyondell Basell公司的影响力为
即禁令实施后近5年来利润下降了18%。禁令实施后对Lyondell Basell公司长期影响力为
即从长期来看,禁令实施后使得Lyondell Basell公司利润降低57%。
3.4. 塑料瓶禁令对可口可乐市场占有率影响力度量
我们从可口可乐公司的官网收集到了2004~2018年可口可乐每年的市场占有率,见表4。

Table 4. Coca Cola’s market share, 2004~2018
表4. 2004~2018年可口可乐的市场占有率
令2004年为第1年,2005年为第2年,以此类推,2018年为第10年,其中禁令颁布年2013年为第9年。以2004~2018年可口可乐公司市场占有率为解释变量,
为分段点,建立分段线性回归模型,得到稳健回归方程如下:
图4为2005~2018年可口可乐公司市场占有率的分段线性稳健回归拟合曲线图。
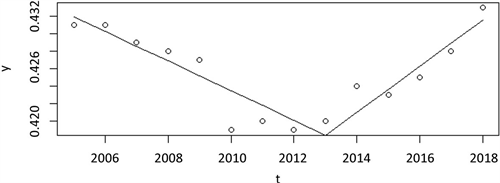
Figure 4. Piecewise linear robust regression fitting curve of the Coca Cola’s market share, 2005~2018
图4. 2005~2018年可口可乐公司市场占有率的分段线性稳健回归拟合曲线图
由分段线性稳健回归方程可知,在2013年实施禁令前,可口可乐的市场占有率为下降趋势,禁令发布后可口可乐的市场占有率为上升趋势。这可能是禁令打压了塑料瓶装水的发展,一部分人选择可口可乐作为塑料瓶装水的替代品,所以导致可口可乐的市场占有率上升。
根据分段线性稳健回归方程可得,禁令实施后近5年来对可口可乐市场占有率的影响力为
即禁令实施后近5年来利润下降了2.5%。禁令实施后对可口可乐市场占有率的长期影响力为
即从长期来看,禁令实施后可口可乐的市场占有率增加2.53倍。
4. 塑料瓶装水禁令综合影响力的定量评估
上面我们给出了禁令对美国PET塑料瓶装水垃圾总量、就业率、PET公司的收入、可口可乐市场占有率等指标的影响力度量。下面我们通过层次分析法来确定这四个指标的权重,从而给出禁令综合影响力的定量评估。
4.1. 构造判断矩阵
在用层次分析法时,最重要的就是将定性分析与定量计算相结合。令
为n个指标。判断矩阵
中的每一个元素
表示指标
相对指标
的重要程度。判断矩阵
若满足
则称A为正互反矩阵;若
则称A为一致矩阵,表示各指标之间满足一致(重要排序)关系。
本文采用Satty 9级标度法构造一个正互反矩阵
。在该标度法中每个数字的含义见表5。

Table 5. Satty 9 scale meaning table
表5. Satty 9级标度意义表
如果要求评价的结果准确,则需要一个权威的判断矩阵。本文采用简答的方法,参考了环保和经济领域的专家建议,对PET塑料瓶装水垃圾总量
、就业率
、美国PET公司的收入
、可口可乐市场占有率
等指标给出了判断矩阵如下:
4.2. 计算权重排序向量与一致性检验
在判断矩阵的构造中,并不要求矩阵完全拥有一致性,这是客观事物的复杂性与人类认识的多样性所决定的,9级标度也决定了三阶以上的判断矩阵是很难满足一致性的。但要求判断有大体上的一致性是应该的,出现甲比乙极端重要,乙比丙极端重要而丙比甲极端重要的判断一般是违背常识的。一个混乱的经不起推敲的判断矩阵有可能导致决策的失误,而且上述各种计算排序权重的方法当判断矩阵过于偏离一致性时,其可靠性程度大大降低。我们将通过一致性检验确定判断矩阵一致性是否可以接受,如果接受,将从判断矩阵中求出被比较指标的排序权重向量。本文采用特征根法计算排序权重向量,即求判断矩阵A的最大特征根
及其对应的右特征向量w,分别称为主特征根与右主特征向量,然后将归一化后的右主特征向量作为排序权重向量。
通过计算可得判断矩阵的最大特征根
及其对应的右特征向量w为
对判断矩阵A进行一致性检验如下:
1) 计算一致性指标
。
2) 查找相应的平均随机一致性指标
,下表给出了1~11阶正互反矩阵的平均随机一致性指标。
3) 计算一致性比例
。当
时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当修正。
说明判断矩阵的一致性是可以接受的。
4.3. 塑料瓶装水禁令的长期综合影响力度量
令“−”号代表负面影响,“+”代表正面影响。我们知道塑料瓶垃圾量增加会给环境带来污染,因此我们取禁令对PET塑料瓶装水垃圾总量的影响力为−3.66。对就业率和PET公司收入带来负增长,因此取禁令对就业率和PET公司收入的影响力分别为−0.2759,−0.57。禁令使得可口可乐市场占有率的增加,显然是正面影响,因此禁令对可口可乐市场占有率的影响力为2.53。表6为禁令对各指标影响力的度量。
这样我们便得到禁令的长期综合影响力为

Table 6. Measurement of the Influence of Prohibition on relevant Indicators
表6. 禁令对相关指标影响力的度量
长期来看,塑料瓶禁令给美国带来的综合影响为负面影响,其综合影响为−99.87%。
5.模型的优缺点
5.1. 模型的优点
本文根据环境、经济等指标时间序列的分段线性特征以及数据量少的实际情况,采用了分段线性回归以及稳健估计进行拟合。在此基础上,提出了塑料瓶装水禁令对环境、经济等指标短期影响力和长期影响力的概念,并给出了短期影响力和长期影响力度量公式。
5.2. 模型的缺点
本文收集到的环境、经济等指标较少,尤其是层次分析的判断矩阵相对主观,对于塑料瓶装水禁令的影响力定量评估存在一定的误差,因此需要尽可能增加与禁令有关的环境、经济指标,这样综合评价更全面,定量评价的结果也更有说服力。