1. 引言
随着分数阶微分方程在物理、化学、工程、生物科学等领域的应用不断推广,国内外各界学者开始广泛关注分数阶微分方程 [1] [2] [3] [4] [5];近几年,越来越多的学者利用各种不动点定理及其它工具,研究了带有各种边值条件的分数阶微分方程解的存在性与唯一性,取得了很多重要的成果 [6] [7] [8] [9]。但有关奇异分数阶微分方程边值问题的研究并不太多。文献 [10] 运用混合单调算子方法和半序集合上的不动点定理证明了奇异Caputo型分数阶微分方程边值问题
正解的存在性,这里f在0和1点是奇异的。文献 [11] 利用Krasnoselskii不动点定理研究了奇异分数阶微分方程系统边值问题
正解的存在性,这里f在0点是奇异的。文献 [12] 利用上下解方法和Schauder不动点定理讨论了分数阶边值问题
正解的存在性,这里f在0和1点是奇异的。
受以上文献的启发,本文将用Krasnoselskii不动点定理和Banach压缩映射原理,研究下面一类带积分边值的奇异分数阶微分方程
(1.1)
正解的存在性,并进一步确定其唯一性。其中
是Riemann-Liouville型分数阶导数,
连续,
,
,
,
(即f在
点奇异),q是
上的非负有界连续函数。
2. 预备知识
在本文的讨论中我们应用了分数阶微分方程的一些基本定义及结论。可以参见文献 [3] [13] [14] [15]。
定义2.1 [3] [15] 函数
的
阶
Riemann-Liouville分数阶积分定义为:
其中f使得上式右侧在
是逐点有定义的,
是通常的Gamma函数。
定义2.2 [3] [15] 函数
的
阶
Riemann-Liouville分数阶微分定义为:
其中
,
表示实数
的整数部分,f使得上式右侧在 是逐点有定义的。
是逐点有定义的。
引理2.1 [3] [15] 设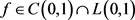 且f的
且f的 阶分数阶导数属于
阶分数阶导数属于 ,那么
,那么
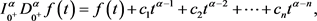
其中 ,其中n是不小于
,其中n是不小于 的最小整数。
的最小整数。
本文在证明分数阶微分方程正解的存在性时,利用Krasnoselskii不动点定理。
引理2.2 (Krasnoselskii不动点定理)设E是Banach空间X的有界闭凸集,S与T为X上的算子,使得
(i) 当 时,有
时,有 ,
,
(ii) S是全连续算子,
(iii) T是压缩映射,
则存在 ,使得
,使得 。
。
引理2.3 (Arzela-Ascoli定理)假设函数族 在区间
在区间 上是一致有界和等度连续的,则存在子函数序列
上是一致有界和等度连续的,则存在子函数序列 在区间
在区间 上是一致收敛的。
上是一致收敛的。
本文在证明分数阶微分方程正解的唯一性时,利用了Banach压缩映射原理。
引理2.4 (Banach压缩映射原理)假设D是Banach空间E的非空闭子集, 是压缩算子,即对任意的
是压缩算子,即对任意的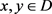 ,有
,有
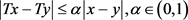 .
.
则存在唯一的 ,使得
,使得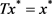 ,即T在D内存在唯一的不动点
,即T在D内存在唯一的不动点 。
。
3. 正解的存在性
定义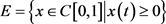 是Banach空间
是Banach空间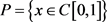 的一个正规锥,E的范数是
的一个正规锥,E的范数是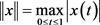 ,定义
,定义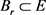 为:
为: 。我们有如下假设:
。我们有如下假设:
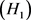 令
令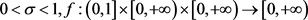 连续,
连续, 假设
假设 在
在 上连续,记
上连续,记 。
。
 存在常数
存在常数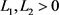 ,使得:
,使得:
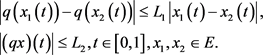
 存在正函数
存在正函数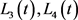 ,使得:
,使得:
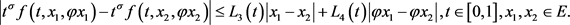
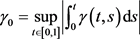
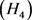 ,
,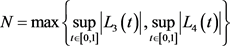 。
。
我们先给出边值问题(1.1)的解的存在性定理:
定理3.1假设 ,
, 成立,且有
成立,且有 ,则边值问题(1.1)至少存在一个正解。
,则边值问题(1.1)至少存在一个正解。
为了证明定理3.1,我们先给出下面三个重要的引理。
引理3.1 若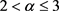 ,
,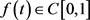 ,分数阶边值问题
,分数阶边值问题
 (3.1)
(3.1)
有唯一解 ,可以表示成:
,可以表示成:

其中格林函数
 (3.2)
(3.2)
证明由引理2.1,方程(3.1)等价于积分方程:

其中 ,由边值条件
,由边值条件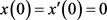 ,可得
,可得 。则
。则


由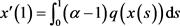 得:
得:

则边值问题(3.1)的唯一解为:
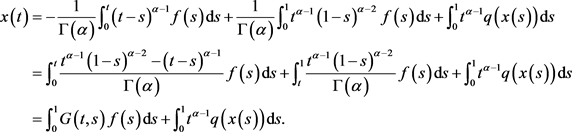
由引理3.1可知,边值问题(1.1)等价于积分方程
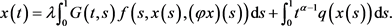
引理3.2由(3.2)式定义的格林函数具有下列性质:
(1)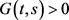 ,对
,对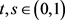 ;
;
(2) ,对
,对 。
。
证明 (1) 当 时,有
时,有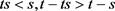 ,又由
,又由 ,知
,知
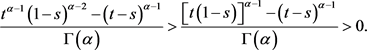
当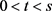 时,显然有
时,显然有

即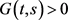 。
。
(2) 对 ,有
,有
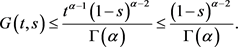
引理3.3设 连续,
连续, ,假设
,假设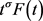 在
在 上连续,则函
上连续,则函
数 在
在 上连续。
上连续。
证明由条件易得 。下面分三种情况讨论:
。下面分三种情况讨论:
情形一: 。对
。对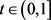 ,由于
,由于 ,存在正数M,使得
,存在正数M,使得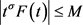 ,则
,则

情形二: 。对
。对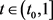 ,
,
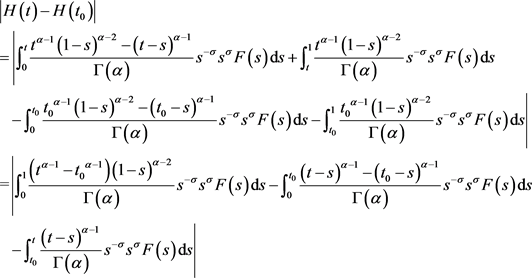

情形三: 。对
。对 ,证明类似于情形二,此处省略。
,证明类似于情形二,此处省略。
接下来我们证明定理3.1:
证明 第一步:证明当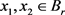 ,有
,有 。
。
令 。在
。在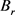 上定义两个算子
上定义两个算子 和
和 ,其中:
,其中:

对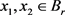 ,有:
,有:


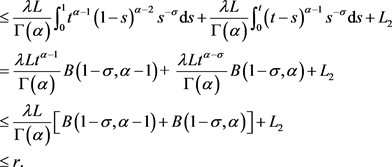
从而

则对于 ,有
,有 。
。
第二步:证明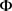 是
是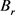 上的压缩映射。
上的压缩映射。
因为 ,所以对于任意的
,所以对于任意的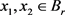 ,有
,有
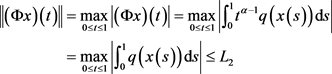
由 ,得到
,得到 。又对任意的
。又对任意的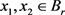 ,有:
,有:

又由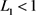 可得
可得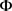 是
是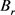 上的压缩映射。
上的压缩映射。
第三步:证明 是全连续算子。
是全连续算子。
对每一个 ,有:
,有:

所以

从而可得 。
。
设 ,由
,由 在
在 上是连续的,故
上是连续的,故 在
在 上是一致连续的,因此,对
上是一致连续的,因此,对 ,当
,当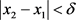 时,使得
时,使得

显然,若 ,则对
,则对 ,有
,有

从而有:
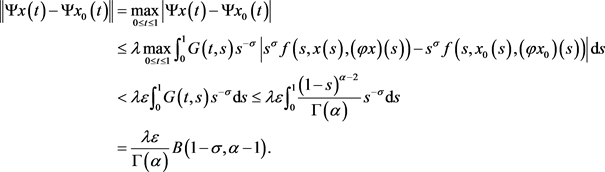
由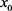 的任意性,可知
的任意性,可知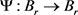 连续。令
连续。令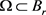 有界,即存在一个正常数a,使得对
有界,即存在一个正常数a,使得对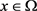 ,有
,有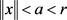 。又
。又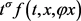 在
在 上连续,由上述证明可得
上连续,由上述证明可得 一致有界。
一致有界。
再证 等度连续。对
等度连续。对 ,取
,取

则对 ,不妨设
,不妨设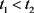 ,使得
,使得 ,有:
,有:



接下来,证明分为两个部分:
(i) 若 ,
,

(ii) 若 ,
,
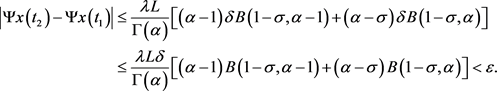
所以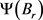 等度连续。由Arzela-Ascoli定理,可知
等度连续。由Arzela-Ascoli定理,可知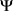 是全连续算子。通过以上证明过程可知Krasnoselskii不动点定理的条件皆满足,从而边值问题(1.1)至少存在一个正解。
是全连续算子。通过以上证明过程可知Krasnoselskii不动点定理的条件皆满足,从而边值问题(1.1)至少存在一个正解。
4. 正解的唯一性
现在,我们给出分数阶微分方程边值问题(1.1)正解的唯一性结果:
定理4.1 如果 ,
, ,
, ,
, 成立,且
成立,且
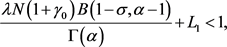
那么边值问题(1.1)有唯一正解。
证明令 。
。
定义:
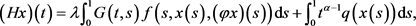
则 。对
。对 ,证
,证 。
。

即 ,则有
,则有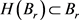 。现在,对
。现在,对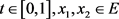 ,有:
,有:

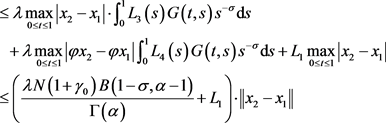
由条件

知F是压缩算子,则由Banach压缩映射原理知,问题(1.1)有唯一的正解。
5. 应用举例
考虑以下带积分边值的奇异分数阶微分方程
 (5.1)
(5.1)
其中 ,
, ,
, 。易知
。易知 连续,
连续,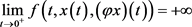 (即f在
(即f在 点奇异),q是
点奇异),q是 上的非负有界连续函数。找到常数
上的非负有界连续函数。找到常数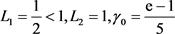 使得:
使得:

同时有 ,使得
,使得
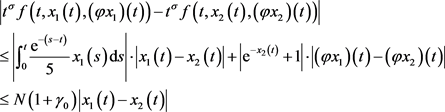
即满足定理3.1,所以问题(5.1)至少存在一个正解。进一步的,当 足够小时,可以满足
足够小时,可以满足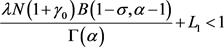 。于是由定理4.1可知,此时问题(5.1)有唯一正解。
。于是由定理4.1可知,此时问题(5.1)有唯一正解。
致谢
作者对审稿人提出的宝贵意见和编辑老师的工作表示衷心的感谢。
基金项目
本文受国家自然科学基金项目(NSFC11501260),江苏高校优势学科建设工程项目(PAPD),江苏高校品牌专业建设工程资助项目 (PPZY2015A013)和江苏省大学生创新创业训练计划项目(201810320015Z)资助。
NOTES
*通讯作者。