1. 引言
随着勘探程度的提高,珠江口盆地白云凹陷钻遇极高温超压地层,深部甜点地层温度达200℃以上,最高可达250℃,这给勘探作业施工带来了巨大的挑战。目前国内外常规的测井和DST测试设备耐温约在150℃~220℃,已经很难满足该区块的作业需求;即使协调到全球数量有限的高温工具(耐温200℃~250℃),也几乎没有作业余量,对作业人员的整体水平要求极高 [1]。在工具耐温短期内无法提升的情况下,攻克高温作业难题需要精细的作业方案设计和作业跟踪决策。作业方案设计包括随钻工具的选型、取舍,高温环境下的作业流程及循环降温方法设计等;作业跟踪决策的内容包括根据实钻地温情况的测试井段选取、作业方案设计、工具准备、资源协调等;而这些的基础就是准确的地层温度测算。
当前国内对地层压力预测的研究较多,而对温度测算的研究却相对较少,且主要集中在对盆地整体地温场的趋势研究 [2] [3],尤其对单井、单构造的地温梯度的预测十分鲜见,这对现场作业施工指导意义有限。
从经济、快速的角度出发,单井预测方法的研究应从钻井过程中获取的温度数据入手。通常海上钻井作业时可以测得的温度数据均为井筒内流体的温度,常见有三种:第一种是循环泥浆温度,即钻进时随钻工具测得的井筒泥浆温度,由于有循环降温作用,该温度数值上远小于真实地层温度;第二种是电缆测井时,测井仪器测得的静止泥浆温度,其中满贯测井的可以得到连续深度点温度,测压取样可以得到单深度点温度,该温度数据相比循环温度更接近地层温度,但因静止时间短,仍处于升温过程中,因此也无法代表地层温度;第三种是DST测试时获得的温度,因射孔后地层流体大量进入井筒且流动时间较长,该温度可近似认为是地层温度。然而DST温度数据在新区块钻井时却较难应用,首先DST测试作业相对较少且数据很难借鉴,其次在整个单井建井周期中,DST测试作业是最后阶段进行的,已经错过了决策时间。
综上所述,利用前两种温度(泥浆温度)数据,建立一套参数简单、应用方便的单井地温梯度预测方法,是解决当前作业难题经济有效的途径。
2. 传统计算方法(Hornor图版法)
运用泥浆温度测算地层温度,国内外文献已经提出了一些方法 [4] - [10],目前运用较为广泛的方法为Hornor图版法 [11],应用公式原理如下(1)式。
(1)
其中
为地层温度,单位℃;
为测得的泥浆温度,单位℃;
为停泵前的连续循环时间,单位h;
为停泵后的泥浆静止时间,单位h;
为岩石热导率,单位W/(mK);H为热供应率。
但是该方法中
和H的值较难获得,在新区块已钻井数据较少的情况下,Hornor图版法难以直接应用。此外,不同井间由于地层条件、泥浆性能、作业情况、井身结构等因素不同,热导相关参数势必存在差异;求取单井的热导相关参数既费周章、时效性较差,且普适性也不好。
总之,Hornor图版法更适用于区域研究性质的钻后总结分析,其成果应用周期性较长,对现场实时作业缺乏指导性和借鉴性。
3. 两种单井预测地温的新方法
为满足一线作业决策及时性的需求,以适用性强为导向,温度预测方法可考虑适当降低精度、简化模型。基于此,设计2种运用单井数据测算地温梯度方法,可以在作业过程中实时推算地温梯度,相比传统方法具有应用性强、时效性高的特点,对作业跟踪及下步快速决策有良好的指导意义。
3.1. 井底单点静止泥浆温度回归法(方法1)
方法1采用的温度数据来源于马龙头上的水银温度计,每进行一次电缆测井可以记录1个温度最大值,通常默认仪器下深最深时读得该温度,再根据作业日报可计算得到泥浆静止时间。一组数据记录3个值
、
、
,代表在
时刻,井深
米处的泥浆温度为
。
3.1.1. 方法思路及计算步骤
前人针对井筒温度场的模拟研究做了很多工作 [12],众多学者在建立数值模型时为了满足工程快速计算的要求,假设井筒内各控制单元间以对流换热方式交换热量,而对于地层则以热传导形式发生热交换。因此,忽略了井下钻柱内和环空流体层间在径向与轴向上热量传递作用,从而建立了目前广泛应用的井筒一维与地层二维空间上的井下传热数值简化模型,该简化模型已被论证满足实际作业的误差要求 [13]。基于此,根据井筒与地层间热量交换机理,可推知当循环结束,某深度点泥浆温度与静止时间关系的曲线有几个特点:① 单调递增;② 增速由快到慢逐渐降低;③ 当静止时间无限大时,泥浆温度趋近于一个极大值。根据这3个特点,可知符合S型曲线特点,选用S型曲线作为升温曲线方程,见(2)式。将作业中记录得到的温度数据,按照升温方程进行回归,求得温度极大值即为所在深度的地层温度。因实际作业过程中测得温度数据的井深略有不同,还需根据地温梯度的计算方法进行一个校正,见(3)、(4)式。
(2)
(3)
(4)
(5)
其中,
代表换算得到的井底温度,单位℃;
代表停泵后的泥浆静止时间,单位h;
代表测得的泥浆温度,单位℃;
代表井底的井深,单位m;
代表测得的泥浆温度的对应井深,单位m;
代表计算地温梯度,单位℃/100m,在本方法中会先赋予1个初始值,后续迭代结束后取值为最终计算结果;
代表海底温度,单位℃,属于已知值;
代表海底泥面深度(补心海拔 + 海水深度),单位m;
代表对应
井深的计算地层温度。
计算步骤如下:
① 电缆测井时测得i组静止泥浆温度数据,(
、
) (
、
)
(
、
)。
② 根据(3)式,给
取一个初始值(可根据地质设计中的区域预测值),将步骤①中测得的数据换算成井底温度和静止时间的组合(
、
) (
、
)
(
、 ),用这几组数据根据(2)式方程进行回归,求得
、
。
),用这几组数据根据(2)式方程进行回归,求得
、
。
③ 在(2)式中令
趋向于无穷大,求得
,即
。
④ 将
代入(4)式求得
,当
时,令
,返回第②步,进行迭代计算。
⑤ 当 时,迭代结束,此时最后一次计算中所得
、
即最终计算结果。
时,迭代结束,此时最后一次计算中所得
、
即最终计算结果。
3.1.2. 应用经验及影响因素分析
1) 至少3个可靠数据点回归出来的方程才具有可参考性。可知该方程本质是S型曲线,在实际应用中,主要关注当
泥浆静止时间趋向于无穷大时的温度极限值,即曲线的右半部分形态,当
趋向于0时,方程并没有对应的实际意义;因此,需要3个以上的数据点才可以较好的刻画出曲线右半部分的形态。在实际应用过程中,3个数据点可以提供较为可靠的预测结果,4个及以上的数据点则计算结果精度较高。
2) 油基泥浆运用该方法进行计算时,所得计算结果可能会明显小于地层真实温度。油基泥浆比热容相对水基泥浆小,钻进时油基泥浆的温度会更高,因此停泵时的起始泥浆温度更高。导致拟合出来的曲线方程右半部分较水基斜率更缓,从而得到相对较低的温度值。通过统计2次油基泥浆井的计算结果,最终计算温度较实际地层温度低了3.2%和4.5%。
3.2. 不同井眼的循环泥浆温度梯度回归法(方法2)
方法2采用的温度数据来源于随钻测井工具,记录的是正常钻进条件下不同井深对应的循环泥浆温度。每个井眼可记录若干数据点,数据密度与随钻测井曲线质量相关。将测得的循环泥浆温度与井深分别作为纵横坐标,投点成图并观察成图规律,从中设计地温梯度测算方法。
3.2.1. 循环泥浆温度的2个特点
1) 每个井眼的循环泥浆温度与井深呈线性关系。
随机选取南海东部15口井的随钻数据,将井深作为横坐标、循环泥浆温度作为纵坐标。观察其成图规律,发现有良好的正相关关系,对两者进行线性方程拟合,R2普遍大于0.95,拟合效果好。仍有小部分井次拟合效果较差或温度曲线不平滑、突变较多。根据相应的井次井深,查找该井的工程日报,分析可知为均出现了钻进停止的情况(下钻循环不充分、起钻、井漏等,见图1)。
综合分析可知,当钻进稳定、循环充分时,随钻温度会随深度进入一个逐步上升的稳态;当出现短起、长起或者各种工程情况停钻,曲线拟合效果将比较差。

Figure 1. Temperature gradient diagram of circulating mud under different working conditions
图1. 不同工况下的循环泥浆温度梯度图
2) 不同井眼拟合出来的直线斜率(即循环泥浆温度梯度)不同;且呈现井眼越小,梯度越大的规律。
对同一口井、不同井眼的循环温度数据进行分析,剔除无效数据后成图(图2),可知小井眼的温度梯度要高一些。从导热原理也可印证这样的结论,井眼越小,井筒中泥浆的降温效果就越差。
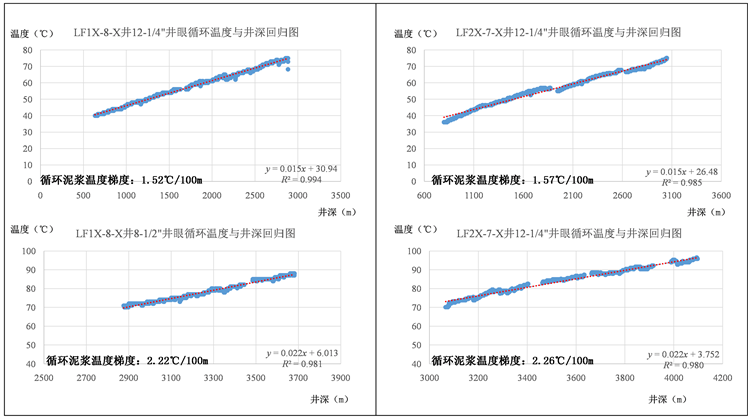
Figure 2. Comparison of temperature gradients of circulating mud in different holes at the same well
图2. 同一井次不同井眼的循环泥浆温度梯度对比图
3.2.2. 方法思路及计算步骤
在海上钻井作业中,只考虑温度升降的情况,整个泥浆循环可以分成两个部分;一部分是升温系统,即泥面到地层的管线;一部分是降温系统,即泥面到钻井平台的管线,海水起到了最主要的降温作用。再结合上述2项特征,可作如下推论:在同一井眼中,当钻进稳定、循环充分时,泥浆循环系统在不断的升温和降温过程中达到动态平衡,形成恒定的泥浆温度梯度;当井眼越小,泥浆温度梯度越接近地温梯度。
据此,可以建立井眼面积与泥浆温度梯度的关联方程,根据热传导原理和已知数据推导,该关联方程可类比液体降温模型 [14] [15],为单调减的指数函数,如(6)式。
(6)
其中
为泥浆温度梯度,单位℃/100m;
为井眼面积,单位
;
、
为常数,且
。
计算步骤。根据实钻过程中的随钻温度数据,求取i组数据(
、
) (
、
)
(
、
),用(6)式回归,求取
、
,当
时,求得的
即计算地温梯度。
3.2.3. 应用经验及影响因素分析
1) 回归出来的曲线方程,R2应至少大于0.95,如R2 < 0.95,则应根据工程日报剔除去无效点之后,再进行拟合。当数据样本较好且筛选得当,多数情况下得到的R2 > 0.98,此时计算结果较准确。
2) 当水深超过300 m,泥浆池升温梯度与循环泥浆温度梯度之比小于0.4时,可直接应用该方法进行计算;否则,则应考虑对排量、ROP变量进行校正。该模型选取井眼截面积作为影响降温效果的决定性因素,隐含了一个前提条件即泥浆循环中降温系统能力远大于升温系统,只有满足上述条件,排量、ROP和井深的影响因素才可以忽略;如降温能力没有远大于升温能力,随着井深变深,升温系统的能力逐步增大,那么方法2模型中动态平衡的基础就没有了。因此水深越深,该方法的应用效果越好;换言之,方法2在深水区钻井有良好的应用效果。
4. 测压取样温度数据的局限性
以上2种计算方法,均没有用到电缆测压取样作业时测得的温度数据(下文简称“测取温度”);因为测取温度有较大的局限性,往往只能用于定性参考,无法应用于定量计算,有如下几个原因:
1) 理论上,测压取样作业是要求从浅层至深层依次进行;而实际作业过程中,由于各深度点物性和井眼规则程度不同,测压取样所需的时间和成功率是不同的。在争分夺秒的测压取样作业中,跳过作业相对复杂的深度点,优先完成流度大、井眼规则的深度点是降低作业风险、提高作业时效的有效手段。这样的作业方式,势必无法保证测取温度记录时由浅至深的规律性,仪器上提下放、降温升温的过程中测得的温度准确性会大大降低。
2) 仪器上的温度计由于是升温调校,由低温环境变换到高温环境得到的数据准确度高;而从高温到低温时,温度计则非常不敏感。
3) 电子电路的温漂和线圈系的温度形变也会在不规律的升降温中产生更多的影响 [16]。
总之,测取温度受影响因素较多,在实际作业中不推荐使用该温度进行计算。
5. BY2-F井实例应用
BY2-F井是白云凹陷钻探的一口深水井,该井水深814.8 m,泥面深度844.1 m,海底温度5.9℃。实钻过程中尝试运用方法1和方法2测算地温梯度,为后续电缆测井、DST测试作业准备提供决策数据。
BY2-F井为一口五开井,三开、四开、五开井眼分别为12-1/4井眼、8-1/2井眼和6井眼。
5.1. 方法1应用
本井在8-1/2井眼(4383 m)和6井眼(5073 m)都进行了电缆测井,根据3.1要求记录得数据见表1。

Table 1. Temperature data sheet of static mud in each hole
表1. 各井眼静止泥浆温度数据表
取初始地温梯度为4.2℃/100m,最终迭代计算得4383 m处地层温度为174.7℃ (图3(a)),5073 m处地层温度208.0℃ (图3(b)),折算成3个地温梯度计算结果见表2。

Figure 3. Last iteration equation diagram of method 1
图3. 方法1最后一次迭代方程图

Table 2. Summary of calculated geothermal gradient data
表2. 计算地温梯度数据汇总表
5.2. 方法2应用
本井在12-1/4井眼、8-1/2井眼和6井眼均有随钻温度数据,根据3.2要求,剔除无效数据后计算得各井眼的循环泥浆温度梯度见表3。

Table 3. Temperature gradient data of circulating mud in each hole
表3. 各井眼循环泥浆温度梯度数据表
根据数据回归计算得地温梯度4.74℃/100m (图4)。

Figure 4. Regression equation chart of method 2
图4. 方法2回归方程图
5.3. DST作业实测温度
最终在DST测试作业中,实测计算得地层温度4.70℃/100m,与上述2个方法计算结果接近,误差在0.85%~2.77%,证实了2种方法在测算地温梯度方面切实可用。
6. 结论
1) 从快速指导作业的角度出发,设计了2种利用泥浆温度测算地层温度的新方法,可以在钻井期间运用泥浆温度快速推算地层真实温度,为作业即时决策提供依据;在BY2-F井中进行运用,取得了良好的效果。
2) 从公式原理可以推论,方法1采用电缆测井期间测量得到的静止泥浆温度,影响温度变化的主要因素为静止起始温度和地层传热,受影响因素较少,因此可应用场景较多,无论在深水井和浅水井都有较高的准确率。
3) 方法2采用钻进期间的循环泥浆温度,该温度受钻井参数、海水深度、地层传热等较多复杂因素影响,简化模型的成立更依赖足够的海水降温能力,因此更适合在深水钻井中应用。如将方法2模型应用于浅水井的计算,需在原模型基础上,考虑用排量和ROP数据对原始温度数据进行校正。