1. 引言
本文主要讨论如下非线性Schrödiger-Kirchhoff型方程
(0.1)
其中
,在一些可解性条件下的基态解的存在性。当
时,
(0.2)
称为Kirchhoff型方程,该模型来源于物理学中描述弹性绳横向振动的长度变化的公式,即经典的D’Alembert波动方程
(0.3)
的行波解,其中u表示位移,
表示外力,b表示初始张力,a表示绳子本身的性质,该式子还广泛应用于生物学中,此时u表示人口密度平均数的排列等 [1] [2]。
近年来,许多学者开始考虑该模型在不同可解性条件下解的存在性、非平凡解、径向和非径向解以及多解性问题,例如文献 [3] 作者利用传播和衍射条件讨论了解的存在性和非存在性。Perera和张志涛在文献 [4] 中用Yang指数和临界群来讨论非平凡解的存在性。毛安民和张志涛在文献 [5] 中通过下降流的变形方法得到多解和变号解。贺晓明和邹文明在文献 [6] [7] 中通过局部极大极小值和喷泉定理得到无穷多解。在文献 [8] 中作者利用局部环绕定理得到解的存在性和多解性。此后,吴鲜等在文献 [9] [10] 中利用山路引理得到高能量解。在文献 [11] 中作者讨论临界和次临界条件下的非平凡解的存在性。在文献 [12] 中作者研究了变号基态解。在文献 [13] 中作者考虑了如下模型
. (0.4)
当
满足 时基态解的存在性,受到(0.4)的启发本文将用Nehari流形的方法处理带有更一般的非线性项的方程(0.1)。
时基态解的存在性,受到(0.4)的启发本文将用Nehari流形的方法处理带有更一般的非线性项的方程(0.1)。
2. 预备知识
本文方程(0.1)中,记
,
,
。
(V)
。
(B)
,且
不恒等于
。
(F1) 存在 ,
,使得对任意
,
满足
,
,使得对任意
,
满足
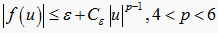 .
.
(F2) 当 时,有
。
时,有
。
(F3) 对任意的 ,有
,有 。
。
(F4) 对任意
,
是严格单调递增的。
本文主要结果如下:
定理1 若条件(V),(B),(F1)-(F4)成立,则方程(0.1)有非平凡的基态解,即存在
是I的临界点,使得 。
。
为书写的简便,我们将使用如下记号:
,其中 。表示Hilbert空间,X空间对应的内积为
。表示Hilbert空间,X空间对应的内积为 ,范数为
,范数为 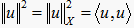 。
。
表示为
上p次可积函数空间,对应的范数表示为
。
方程(0.1)对应的泛函
.
若对问题(0.1)的任意非平凡解w有
,则问题(0.1)的弱解即为基态解。
定义Nehari流形为
.
泛函的微分形式为
.
若 满足
, 那么
满足
, 那么  记为(0.1)的基态解。
记为(0.1)的基态解。
定义如下形式的辅助泛函:
 .
.
同理定义流形
.
定义
,
,
,
.
其中
.
.
引理1 假设满足条件(V),(B),(F1),(F2),(F4),存在
,有
,则对任意
有
。
证明:对任意的, (其中
由
,
,任意
给出),由(F1) (F2)可知,存在常数
,使得
(其中
由
,
,任意
给出),由(F1) (F2)可知,存在常数
,使得
. (1.1)
和
 . (1.2)
. (1.2)
且(F4)意味着
,因此存在常数,对充分小的
,
.
对所有的 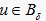 ,其中
,因此,
。 □
,其中
,因此,
。 □
类似于文献 [14],引入同胚映射
和泛函
,定义如下
,
.
其中
。
引理2 (a) ( [15] 引理2.3)假设满足条件(V) (B) (F1)~(F4),对任意的
,使得
,若存在
使得当
时,有
,当
时,有 。
。
(b) 假设满足条件(F2)和(F4),在X中有
弱收敛到u,且
,则对任意的数列 ,当
时,
,当
时, ,有
,那么有
。
,有
,那么有
。
定理2 假设满足条件(V),(B),(F1)-(F4),则有 ,其中c为I的临界值。
,其中c为I的临界值。
证明:1) 由假设可知,对任意
,存在唯一
,使得 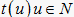 。当
时,可在
。当
时,可在 处得到
的最大值
处得到
的最大值
.
t是连续的,且
是X中单位球面的同胚映射,对(F4)进行积分可知存在常数
,使得
取适当的 ,令
,
,令
,
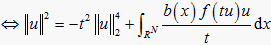 .
.
则由引理2知,存在唯一 ,使得
,且有
,为了证明
,使得
,且有
,为了证明 的连续性,假设存在序列
,容易得到
是有界的,若存在
的子列收敛到
,则
的连续性,假设存在序列
,容易得到
是有界的,若存在
的子列收敛到
,则 ,再由X的单位元到N中的连续映射
是反向的拉回映射
,即可得到
,再由X的单位元到N中的连续映射
是反向的拉回映射
,即可得到
.
因为对于
时,
,可以得到
,流形N将X分为两个部分,由(F1)和(F2)可知包含原点的分量也包含了原点的邻域,且 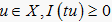 ,因为
,对于
,因而,对于每一个
穿过N且
。
,因为
,对于
,因而,对于每一个
穿过N且
。
为了证明c是I的临界点,即证I满足PS条件即可 [16],
,有(F1)和(F2)存在
,使得
.
可以得到
.
由引理可知I满足PS条件。 □
命题 假设满足条件(V),(B),(F1)~(F4),那么有以下结论成立:
(a)
是弱下半连续的;
(b) 若
是
的PS序列,则
是I的PS序列;
(c) 若w是
的临界点,当且仅当
是I的非平凡临界点。
引理3 假设满足条件(V),(B),(F1)~(F4),则方程(0.1)的极限形式存在非平凡解。
证明:首先证明(0.1)的极限方程的基态解 [17],等价于泛函
限制在流形
上的极小值问题,那么由假设
知,
是一个局部严格极小值点,
,假设
为
的极小化序列,应用Ekland变分原理 [17] 知,假设
,由命题(b)知若
是
的PS序列,则
是
的PS序列,那么 ,其中
,同样的由命题(c)(用
替换I结论仍然成立)知若v是
的临界点,当且仅当
是
,其中
,同样的由命题(c)(用
替换I结论仍然成立)知若v是
的临界点,当且仅当
是 的非平凡临界点,其中
,即
,则
。
的非平凡临界点,其中
,即
,则
。
先证
在X中是有界的,若不然,可设当
时,
,令
,则存在
的子列,仍将其记为
,那么在X中有
弱收敛于w,在
中有
收敛于w,对任意的
,有 几乎处处收敛到
,由Sobolev嵌入定理可知
在
几乎处处收敛到
,由Sobolev嵌入定理可知
在 上是有界的,即
,不是一般性,我们可以假设
,
上是有界的,即
,不是一般性,我们可以假设
,
(i) 若
,由条件(F1)和(F2)知,对任意的
,
. (1.3)
. (1.4)
因为
,即
,又序列
在
上是有界的,则存在
,当
,有
. (1.5)
因此,对任意的 ,
,再由范数的等价性可知,对任意的
,
,再由范数的等价性可知,对任意的 ,当
时,
,当
时, ,可以得到
,可以得到
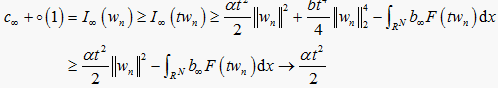 (1.6)
(1.6)
矛盾(可取
)。
(ii) 若 ,即在
中,有
不收敛于0,由Lions紧性引理 [18] 可知,存在
,使得
,即在
中,有
不收敛于0,由Lions紧性引理 [18] 可知,存在
,使得
. (1.7)
再有泛函
和流形
的平移不变性可知
是不变的,不妨设
是有界的,若不然将
平移可以得到。由假设在
中有
收敛于w,那么式子(1.7)意味着
,由引理2(b)和Fatou引理得
. (1.8)
可得
,与命题(b)
矛盾,则
在X中是有界的,那么我们可以其找到子列仍记为
,那么在X中有
弱收敛于
,在
中有 收敛于
,对任意的
,有
几乎处处收敛到
,在由命题(a)
收敛于
,对任意的
,有
几乎处处收敛到
,在由命题(a) 是弱序列连续的可知
(即
)。
是弱序列连续的可知
(即
)。
其次,我们将证明
。
类似于前面的证明我们假设
,若
,由条件(F1)和(F2)得
. (1.9)
类似(i)的证明有
.(1.10)
因此
(1.11)
意味着
,与
和
矛盾,则可得
,即在 中有
不收敛于0,根据Lions紧性引理可知存在
,使得
中有
不收敛于0,根据Lions紧性引理可知存在
,使得
. (1.12)
因为在
中有 ,则由(1.12)可知
,又因为
,所以
,再由
的定义知
,则由(1.12)可知
,又因为
,所以
,再由
的定义知
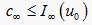 . (1.13)
. (1.13)
结合Fatou引理
. (1.14)
结合(1.13)和(1.14)可得
,因此得到
是(0.1)极限形式的一个弱解。
3. 主要定理的证明
定理1的证明:
类似于引理3的证明,设
满足
,且 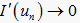 ,假设
在X中是有界的,若不然,令
,则可以假设在X中有
弱收敛到z,在
中有
收敛到z,对任意的
有
几乎处处收敛到
。因此,存在序列
,使得
,假设
在X中是有界的,若不然,令
,则可以假设在X中有
弱收敛到z,在
中有
收敛到z,对任意的
有
几乎处处收敛到
。因此,存在序列
,使得
. (2.1)
否则,由Lions紧性引理可得 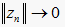 ,则由(1.5)知,对任意的
,则由(1.5)知,对任意的 ,有
,有
 . (2.2)
. (2.2)
由
,我们可以得到
(2.3)
矛盾,那么(2.1)成立,接下来不妨设
,不妨设
是有界的。由假设在
中有 收敛于z,那么
,由引理2(b)和Fatou引理得
,与命题(b)
矛盾,则
是无界的,可假设
,令
,由于
,因此存在
,使得在X中有
弱收敛到
,在
中有
收敛到
,且对任意的
有
几乎处处收敛到
,由(2.1)知
收敛于z,那么
,由引理2(b)和Fatou引理得
,与命题(b)
矛盾,则
是无界的,可假设
,令
,由于
,因此存在
,使得在X中有
弱收敛到
,在
中有
收敛到
,且对任意的
有
几乎处处收敛到
,由(2.1)知
 . (2.4)
. (2.4)
那么有
,结合(F2)和(F4),存在
对任意的
,有
.(2.5)
得到矛盾。
综上可得
在X上是有界的,则我们可以假设存在u使得在X中有
弱收敛到u,在
中有
收敛到u,且对任意的
有
几乎处处收敛到
,结合(F1)和(F2)可得
。
下证 u≠0。有
在X中是有界的,则有
使得
 . (2.6)
. (2.6)
否则,由Lions紧性引理可知
.(2.7)
那么
是有界的,若不然可找到
的无界子列,仍记为
,且
,令
,同样地,在X中有
弱收敛到
,在
中有
收敛到
,且对任意的 有
几乎处处收敛到
,由(2.6)可知
有
几乎处处收敛到
,由(2.6)可知
.
,结合
和 ,则
,由命题(a)
是弱序列连续的,可以得到,
,则
。同理,由条件F (3)和Fatou引理可得
,则
,由命题(a)
是弱序列连续的,可以得到,
,则
。同理,由条件F (3)和Fatou引理可得
.
矛盾。故可得 是有界的,不妨设
,由(2.6)知
是有界的,不妨设
,由(2.6)知
 .
.
又由于在
中有 收敛于u,则
,且
收敛于u,则
,且 ,故有
,因此
,结合条件F (3)和Fatou引理得
,故有
,因此
,结合条件F (3)和Fatou引理得
.
综上可得
,故u是方程(0.1)的基态解。 □