上证电信指数预测研究——基于人工神经网络模型

Research on Shanghai Telecom Index Forecast—Based on Artificial Neural Network Model

摘要: 人工神经网络具有极强的非线性动态处理问题的能力，股票走势由多个非线性因素影响，因此本文试图借助Python的数据分析功能，使用人工神经网络模型对上证电信指数走势进行预测，并将预测结果与实际结果进行对比，判断人工神经网络在股票预测中的精确程度。

Abstract: Artificial Neural Network has the strong ability of nonlinear dynamic processing problems, stock movements by many nonlinear factors, so this paper tries to use Python data analysis function, the use of artificial neural network model to forecast the Shanghai telecom index trend, and the prediction results compared with the actual result, judgment of the Artificial Neural Network in stock forecasting accuracy.

1. 引言

人工神经网络(Artificial Neural Network，即ANN)，是20世纪80年代以来人工智能领域兴起的研究热点。它是一种运算模型，由大量的节点(或称神经元)之间相互联接构成。每个节点代表一种特定的输出函数，称为激励函数(activation function)。

股票是热门投资方式之一，根据中国结算2月17日公布的数据显示，A股市场投资者人数为16,055.30万人，大约是每十个人中就有一个股民，说明中国股票市场规模庞大。而炒股的人最关心的就是股价，股价随着市场变动而变化，如果能够预测股票走势，这将对投资者投资决策产生重大帮助。

人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。而股票价格易受到多个非线性因素影响，所以本文拟采用人工神经网络对上证电信指数股票走势进行预测。

2. 国内研究现状

国内学者深入研究了人工神经网络，已经取得了很大的进展，并在多个领域应用人工神经网络解决了很多难以解决的问题。

朱顺泉、李一智 [1] 于2002年在建立公司债券财务质量指标体系的基础上，提出了用神经网络对公司债券财务质量的综合评价方法，并利用数据进行了实证，得到了较好的评价结果。

孔维娜、李跃进、李双异 [2] 等于2012年以辽宁省彰武县为研究对象，在AHP-模糊评价方法的基础上建立耕地地力的ANN-产量定量评价模型。发现与传统方法相比，模型不需要确定权重，并且能够反映耕地地力评价的非线性特征，消除了传统方法确定权重时人为因素的影响，增加了评价结果的客观性。贺昌政、俞海 [3] 于2001年通过实例证明，BP神经网络主成分分析模型在复杂经济系统模拟预测中比通常的BP神经网络模型有较好的效果。

赵瑞莹、杨学成 [4] 于2008年建立了基于BP人工神经网络的农产品价格风险预警模型，并以生猪为例进行了验证。发现生猪价格风险预警模型的成功构建，说明了基于BP人工神经网络的农产品价格预警模型是切实可行的。于佳 [5] 于2006年使用BP神经网络预警分析方法作为房地产行业风险预警模型，用以判断房地产行业风险警度并预测其发展趋势。并利用上述模型以哈尔滨市房地产业为对象进行应用，研究表明2005年哈尔滨房地产行业发展比较稳定，处于正常行业上升阶段，据此提出了相应的建议。

彭涛 [6] 于2009年借助神经网络极强的非线性动态处理问题的能力，将其引入房地产价格评估领域，创建了基于神经网络的房地产价格评估模型，并发现房地产影响因素与其成交价格之间复杂的客观规律。高琴 [7] 于2007年建立BP神经网络模型，以某个股实际收盘价为原始数据样本，对股票价格进行了短期预测，并计算出预测值和实际值的误差。发现该模型收敛速度快，预测精度高。

汤江龙 [8] 于2006年研究发现好的人工神经网络模型可以提高模型仿真质量与效率，利用规划学习样本和合适的模型结构参数，可以减少试验次数，缩短仿真时间，提高仿真预测的精度。

胡静 [9] 于2007年运用人工神经网络理论，构建了股票价格预测模型体系，提出了基于遗传算法的神经网络和基于粒子群算法的神经网络的系统建模方法，提高了系统预测准确度。高攀 [10] 于2017年利用人工神经网络学习能力和非线性映射能力较强的特点，将神经网络模型引入到二手房价格评估过程中，建立适用于重庆市巴南区的二手房价格评估神经网络模型，提高评估结果的准确性，促进房地产估价行业的发展。

综上所述，可以发现，人工神经网络运用的领域广泛，在预测股票走势方面也有大量前人的研究成果，因此该研究方向是可行的。本文将在前人研究的基础上，使用人工神经网络模型，对上证电信指数进行预测，并将预测结果于实际情况进行对比，判断人工神经网络在股票预测中的精确程度。

3. 人工神经网络

人工神经网络(Artificial Neural Network，即ANN)，是20世纪80年代以来人工智能领域兴起的研究热点。它从信息处理角度对人脑神经元网络进行抽象，建立某种简单模型，按不同的连接方式组成不同的网络。

人工神经网络能自动从历史数据中提取有关经济活动中的知识，可以克服传统定量预测方法的许多局限以及面临的困难，同时也能避免许多人为因素的影响，因而在股市预测模型建造的合理性以及适用性方面都具有其独特的优点。

3.1. 算法原理

根据阎虎勤研究 [11] 表明，由于人工智能求解问题太过复杂，可以假设本文所讨论的ANN过程只有两层：输入层和输出层。这样就可以将复杂的问题简化为求解一个多元一次方程。

本文不打算采用一般的回归方程求解模式来求解，而是要采用迭代法来求解，通过一步步地迭代逼近，直到所得到的最终结果收敛于一个可接受的值。这个可接受的值，就是指方程的解，与目标输出值之间的误差小于某一个误差范围，即不超过某个值，例如0.001等。

如图1所示，就好比人类的神经元之间进行信号传递过程中：一个单一的神经元在发送一个信息给另外一个神经元时，对于接收方神经元来说，如果这些来自一个或者多个神经元的信息，经过加权合计，达到了足够的强度而超过了一个门限值(exceeds a threshold)，就会触发这个信息继续向前传递(transmission)，这个被激活(activation)的信息，将被传递给下一个神经元。

Figure 1. ANN learning process computer algorithm for two-layer ANN with only input and output layers

图1. 只有输入层和输出层的二层人工神经网络ANN学习过程计算机算法

假设A表示输入变量矩阵，它包含了n个子变量，每个子变量包含m个观测值，输入变量既可以被看成是一个矩阵，也可以被看成是一个行向量。如公式(1)所示：

$A=\left(a_1\cdots a_n\right)=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{m1}& \cdots & a_{mn}\end{array}\right)$ (1)

假设Y表示输出变量矩阵，它包含了1个子变量，具有m个观测值。如公式(2)所示：

$Y=\left(\begin{array}{c}{y}_1\\ ⋮\\ y_m\end{array}\right)$ (2)

本文采用了有常数项扰动的线性方程组，实际上是一个非齐次线性方程组(多元一次方程)。如公式(3)所示：

$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n+h=y_1\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n+h=y_2\\ ⋮\\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n+h=y_m\end{array}$ (3)

方程组的矩阵表示形式为：

$A_{mn}{X}_{n1}+I_{m1}h=Y_{m1}$ (4)

由于二层人工神经网络方法没有直接求解方程组，于是便定义了一个激活函数f，把直接求解转化成了间接求解，即求解方程：

$f\left(A_{mn}{X}_{n1}+I_{m1}h\right)=Y_{m1}$ (5)

激活函数通过变换，把原来的线性方程组转换成了一个新的线性方程组。

3.2. 激活函数

边际产出，其实质就是对于生产函数求一阶偏导数：

在神经网络运算中，激活函数十分重要。激活函数是来向神经网络中引入非线性因素的，通过激活函数，神经网络就可以拟合各种曲线。

本文使用了sigmoid函数，即值域介于0和1之间的激活函数，这是一类增长函数。

$f\left(x\right)=\frac{1}{1+{\text{e}}^{-x}}=\{\begin{array}{l}0x\to -\infty \\ \frac{1}{2}x\to 0\\ 1x\to +\infty \end{array}$ (6)

显然如图2所示，该函数的定义域为 $x\in \left(-\infty ,\infty \right)$，而值域为 $y\in \left(0,1\right)$。

该函数的导函数为：

$f^{\prime }\left(x\right)=\frac{{\text{e}}^{-x}}{{\left(1+{\text{e}}^{-x}\right)}^2}$ (7)

由于该函数的值域上限为1，所以，当作为因变量的样本值超过1时，就不能直接使用该函数作为激活函数。

Figure 2. Sigmoid function and derivative graph

图2. Sigmoid原函数及导数图形

为了排除该限制，本文将一个非负序列 $\left\{y_1,y_2,\cdots ,y_i,\cdots ,y_n\right\}$，设定一个上限值 $K>0$，使得：

$M={\max }_{i=1,2,\cdots ,n}\left\{y_1,y_2,\cdots ,y_i,\cdots ,y_n,K\right\}$ (8)

取出因变量的样本值中最大的数，然后对原样本值重新进行处理，使得：

$y_i=\frac{y_i}{M},\left(i=1,2,\cdots ,n\right)$ (9)

那么，这样得到的新序列一定是符合激活函数值域要求的。而且，在取得最优解之后，如果要求得原序列的预测值并且进行图示，则必须还原序列为：

$y_i=M{y}_i,\left(i=1,2,\cdots ,n\right)$ (10)

经过以上处理，样本序列既符合几何函数值域要求，其预测目的也不受任何影响。

3.3. 求解过程

本文使用二层人工神经网络预测股票收盘价的算法步骤如下：

1) 正向方程求解逻辑。

假设输入样本为 $A=\left[x_1,x_2,\cdots ,x_n\right]$，输出样本为 $Y=\left[y_1,y_2,\cdots ,y_n\right]$。假设线性方程组的表现形式如下：

$U_{m1}=A_{mn}{X}_{n1}+I_{m1}h$ (11)

其中， $X_{n1}$ 是方程的解，h是常数项。经过sigmoid激活函数 $f\left(u\right)$ 作用之后，方程式可以表示为：

$f\left(U_{m1}\right)=Y_{m1}$ (12)

假设 $E_{m1}$ 为误差项，满足关系式：

$E_{m1}=Y_{m1}-f\left(U_{m1}\right)$ (13)

如果 $E_{m1}=0$，则 $X_{n1}$ 和h就是带有激活函数的方程的解。

一言以蔽之，方程的求解问题就是寻找满足以下关系式的 $X_{n1}$ 和h的最优解：

${\min }_{X_{n1},h}\left\{E_{m1}=Y_{m1}-f\left(A_{mn}{X}_{n1}+I_{m1}h\right)\right\}$ (14)

2) 通过反向传播(Backward Propagation, BP)调解，求最优解。

如果误差项的值不为零，即 $E_{m1}\ne 0$，那么，通过对解 $X_{n1}$ 和h增加调节量：

$X_{n1}=X_{n1}+{\delta }_{n1}$ (15)

$h=h+\tau$ (16)

如果经过激活函数调解之后能够使误差项等于零，则满足条件：

$f\left(A_{mn}\left(X_{n1}+{\delta }_{n1}\right)+I_{m1}\left(h+\tau \right)\right)=f\left(U_{m1}+A_{mn}{\delta }_{n1}+I_{m1}\tau \right)=Y_{m1}$ (17)

那么，原方程的求解问题就被转化为如下问题：

${\min }_{X_{n1},h,{\delta }_{n1},\tau }\left\{E_{m1}=Y_{m1}-f\left(A_{mn}{X}_{n1}+I_{m1}h+A_{mn}{\delta }_{n1}+I_{m1}\tau \right)\right\}$ (18)

按照泰勒(Taylor)展式，对激活函数按照一阶泰勒展式展开，则有：

$f\left(U_{m1}+A_{mn}{\delta }_{n1}+I_{m1}\tau \right)=f\left(U_{m1}\right)+f^{\prime }\left(U_{m1}\right)\left[A_{mn}{\delta }_{n1}+I_{m1}\tau \right]=Y_{m1}$ (19)

那么就有：

$f^{\prime }\left(U_{m1}\right)\left[A_{mn}{\delta }_{n1}+I_{m1}\tau \right]=Y_{m1}-f\left(U_{m1}\right)=E_{m1}$ (20)

3) 调节变量 ${\delta }_{n1}$ 和 $\tau$ 取值的确定

由于有关系式：

$A_{mn}{\delta }_{n1}+I_{m1}\tau =\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}$ (21)

假如 $\tau =0$，则有：

$A_{mn}{\delta }_{n1}=\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}$ (22)

$A_{mn}^{\text{T}}{A}_{mn}{\delta }_{n1}=A_{mn}^{\text{T}}\left[\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}\right]$ (23)

${\left(A_{mn}^{\text{T}}{A}_{mn}\right)}^{-1}{A}_{mn}^{\text{T}}{A}_{mn}{\delta }_{n1}={\left(A_{mn}^{\text{T}}{A}_{mn}\right)}^{-1}{A}_{mn}^{\text{T}}\left[\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}\right]$ (24)

${\delta }_{n1}={\left(A_{mn}^{\text{T}}{A}_{mn}\right)}^{-1}{A}_{mn}^{\text{T}}\left[\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}\right]$ (25)

假如 $\tau \ne 0$，从而，常数项的调解量就可以是：

$I_{m1}\tau =\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}-A_{mn}{\delta }_{n1}$ (26)

$I_{m1}^{\text{T}}{I}_{m1}\tau =I_{m1}^{\text{T}}\left\{\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}-A_{mn}{\delta }_{n1}\right\}$ (27)

${\left(I_{m1}^{\text{T}}{I}_{m1}\right)}^{-1}{I}_{m1}^{\text{T}}{I}_{m1}\tau ={\left(I_{m1}^{\text{T}}{I}_{m1}\right)}^{-1}{I}_{m1}^{\text{T}}\left\{\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}-A_{mn}{\delta }_{n1}\right\}$ (28)

整理后得到

$\tau ={\left(I_{m1}^{\text{T}}{I}_{m1}\right)}^{-1}{I}_{m1}^{\text{T}}\left\{\frac{E_{m1}}{f^{\prime }\left(U_{m1}\right)}-A_{mn}{\delta }_{n1}\right\}$ (29)

这样，只要重复上述过程，则可以逐步迭代，直到取得增加了调节量的 $X_{n1}$ 和h的值，也就是具有扰动项的方程组的最优解。

3.4. 利用二层人工神经网络算法进行股票指数预测

假设股票指数样本序列为：

$S=\left\{y_1,y_2,\cdots ,y_{n-1},y_n,y_{n+1},\cdots ,y_{n_0},y_{n_0+1},\cdots ,y_{N_1}\right\}$ (30)

为了进行模拟，我们采用时间序列的向量自回归(Vector Auto Regression, VAR)模型来进行预测，当 $m=n_0-n+1$，取 $i=0,1,\cdots ,m-1$，则通项公式可以写为：

$y_{1+i}{x}_1+y_{2+i}{x}_2+\cdots +y_{n-1+i}{x}_{n-1}+h=y_{n+i}$ (31)

该模型采用了一个自循环矩阵，使得输入矩阵和输出矩阵来源于同一个样本数据序列，但是在排列上有所区别。

如果将激活函数作用于矩阵方程，则有：

$f\left(A_{mn}{X}_{n1}+I_{m1}h\right)=Y_{m1}$ (32)

本文采用该模型进行实际编程时，如图3所示，对样本数据进行适当分割处理，以便能够检验最优解的效果。

Figure 3. Schematic diagram of the selection of variables in the sample window of the ANN prediction program

图3. 人工神经网络预测程序样本窗口变量取舍示意图

其中样本总数为 $N_1$，被区分为模拟窗口 $n_0$ 和预测窗口 $NN=N_1-n_0$。对于模拟窗口 $n_0$，如果输入矩阵列数为 $n-1$，那么行数则为 $m=n_0-n+1$。对于全样本窗口 $N_1$，如果输入矩阵列数为 $n-1$，则行数则为 $M=N_1-n+1$。

4. 数据处理与预测结果

4.1. 数据的获取与假设

本文采用的数据是利用Python的Akshare函数库从新浪财经获取，数据包括2015年1月5日至2020年4月22日的上证电信指数数据。因此本文提出以下假设：1) 数据来源真实有效；2) 研究期内并未出现大的股票市场波动。

在人工神经网络的算法中，对于激活函数的自变量求解，是先随机给自变量赋予一个初始值，不断为自变量增加调节量来进行迭代，从而求出那个使得误差项最小的自变量。因变量是上证电信指数，根据公式(36)计算出的指数增长率：

$B_t=\frac{A_1}{A_1}\cdot \frac{A_t}{A_{t-1}}$ (33)

其中： $A_1$ ——第1天的上证电信指数；

$A_t$ ——第t天的上证电信指数；

$B_t$ ——第t天的上证电信增长指数。

4.2. 参数含义

如表1所示，调整后的R²能对添加的非显著变量给出惩罚，也就是说随意添加一个变量不一定能让模型拟合度上升，因此我们参考调整后的可决系数R²来评价拟合优度。不管是指数预测还是指数增长率的预测的调整后的可决系数R²均大于0.9，可见，拟合优度较高，拟合曲线较为平滑。

Table 1. Goodness of fit between index forecast and growth index forecast

表1. 指数预测和增长指数预测拟合优度

4.3. 预测结果分析

选取以上指标之后，在Python程序中进行预测值拟合分析，如图4和图5所示。在预测期内，上证电信指数预测值的拟合程度较高，样本曲线和拟合曲线在预测期内能保持一致，没有出现大幅波动，这说明了二层人工神经网络模型的拟合性较强，可预测性较强。

Figure 4. Fitting results of the predicted value of Shanghai Telecom Index in the prediction period

图4. 预测期上证电信指数预测值拟合结果

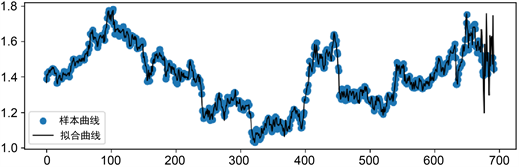
Figure 5. Fitting results of the forecast value of the growth index of Shanghai Telecom in the forecast period

图5. 预测期上证电信增长指数预测值拟合结果

4.4. 预测实际检验

因为对于股票指数预测来说，对于上涨或者下跌趋势的预测往往比股票指数值接近更有意义，所以，本文对于预测效果进行如下处理。

假设集合 $\left\{y_t\right\}$ 由序列原值组成，集合 $\left\{{\hat{y}}_t\right\}$ 由序列预测值组成，那么，如果表示二者增长趋势的变量之间的乘积大于零，则证明预测值与原值的变化趋势一定是一致的，即会发生同升或者同降的情况：

$Tren{d}_t=\left(\frac{y_t}{y_{t-1}}-1\right)\left(\frac{{\hat{y}}_t}{{\hat{y}}_{t-1}}-1\right)>0$ (34)

这种情况，证明预测结果是比较理想的。

假设在区间 $\left(n_0,N_1\right)$ 内，总共 $N_1-n_0$ 个样本值，出现 $Tren{d}_t>0$ 次数为Positive，而出现 $Tren{d}_t<0$ 次数为Negative，则具有一致趋势的百分数为：

$SameTrend=\frac{Positive}{N_1-n_0}\times 100\%$ (35)

具有相反趋势的百分数为：

$DifferentTrend=\frac{Negative}{N_1-n_0}\times 100\%$ (36)

因此本文预测结果如下所示：

Table 2. Actual forecast test of Shanghai Telecom Index and growth index

表2. 上证电信指数和增长指数实际预测检验

Table 3. Forecast results of Shanghai Telecom Index and growth index

表3. 上证电信指数和增长指数预测结果

从表2和表3中可以发现，在预测窗口期间，指数预测与指数增长率预测均高于0.5，说明，预测结果较为理想。

5. 结论

本文采用二层人工神经网络对上证电信指数进行分析预测，用实证分析证明了该模型的可预测性。从预测拟合结果来看，所得模型的误差较小，预测值的准确度高达60%，结果与实际值的拟合程度较高。可见，采用人工神经网络模型对股价预测的可靠性较强，这为股票投资者提供了具有实际意义的参考数值，以更加创新的方式解构了函数预测指数的理论体系。

基金项目

本论文得到了厦门国家会计学院2019年“云顶课题：YD20190101Python财务数据分析”项目的支持。