曲阜市电动公交车的运行路线及换车策略建模分析

Modeling and Analysis of Operation Route and Change Strategy of Electric Bus in Qufu

摘要: 伴随着社会各界对城市污染问题的日益关注，电动公交车因其噪音低，零排放等优点被广泛使用。为制定电动公交车合理的调度方案，论文基于历史数据，从乘客和公交公司的利益出发，以平均满载率、乘客的舒适度和满意度为目标，建立调度方案的优化模型，通过对模型的求解，给出了理想发车时刻表和最少车辆数。

Abstract: With the increasing attention of the society to the problem of urban pollution, electric buses are widely used because of their low noise and zero emission. To formulate a reasonable scheduling scheme for electric buses, the paper based on historical data, from the interests of passengers and bus companies, with the average full load rate, passenger comfort and satisfaction as the goal, the optimization model of the scheduling scheme is set up to give the ideal departure schedule and the minimum number of vehicles by solving the model.

1. 引言

在城市交通问题日益严峻的社会中，先进的智能公交调度系统是公交企业运营管理的核心内容 [1]，对公交调度进行优化设计要充分协调乘客和公交公司的利益冲突 [2]。现在有许多研究电动公交车的课题，比如，对电动公交车电池续航预测研究 [3]、对计及电池损耗的电动公交车参与V2G的优化调度策略研究 [4]、对纯电动公交车电传动系统研究 [5]、对电动公交车电源管理系统的研究 [6] 等等。当然，研究内容同样非常热门的便是电动公交车辆的调度计划。很多算法已经可以相对比较顾及多方面利益，比如扬扬等人基于列生成算法的电动公交车辆调度计划 [7]。本文在借鉴了许多关于数学建模的书籍与实际研究现状的基础上，从最大客运量、调度不同、乘客满意度的不同方面建立了数学模型，实现公交集团以及乘客的最佳满意度，为公交公司制定科学、合理的运营提供了借鉴作用 [8]。

2. 公交车调度模型

我们将公交车路线分为上行和下行两个方向，上行则具体划分为14站，下行是13站。研究从早6:30开始至晚18:30，以1小时为时间间隔，则有12个时间段，分别统计每个时间段公交车各站上下车人数。设一辆公交车限载100人，据调查，在此路线上公交车行驶的平均速度为20 km/h，考虑到公交车的运营情况以及车辆分配问题，一般情况下乘客待车时长不得高于10分钟，早上高峰期要尽量少于5分钟，车辆载满率应大于50%低于120%。基于上述数据和要求，于是我们规划了一个在工作日实行且方便操作的公交车调度方案，内含上行和下行方向的发车时间表，一天内发行的此路线上的总车辆数，以及此计划中使得公交车公司和乘客双方得到称心如意结果的利益满意程度指标，然后考虑怎样将这个抽象笼统的调度问题转化为一个具体详细实用的数学模型。

若单方面考虑公交车公司经济利益最大化，那么我们只需要考虑提高公交车的满载率，然而，乘客的舒适度就会伴随着公交车满载率增加的过程中而减少。如果我们仅仅关注到乘客出行便利，那么只需要添加公交车辆的运行次数，但是，这时公交车公司的利益不会达到最优化，所以我们仅仅考虑某一方面是不可取的，它们是相互冲突的，我们需要在乘客的满意程度与公交车公司的利益两个因素中找出一个最合理的调度策略，使得两者的满意度能达到相对最优化 [9]。

制定公交车调度方案，由于影响因素较多，且许多因素都是随机的，因此要综合多方面因素考虑。为了把握核心，理解中心要素，使建立模型和求解模型变得更加简便，我们做出以下假设：

1) 两辆公交车发车相差时间要取整数，并且在行驶过程中，相互追赶不上。

2) 假设在各个时间段内各站点的等待上车的人数服从泊松分布且数据真实可靠。

3) 交通良好，无堵车现象，路面平坦，无车辆损毁现象以及无其它意外情况 [10]。

4) 公交车在行驶过程中做匀速运动，公交车的发车时间固定，严格按照时刻表，发车数量也固定 [11]。

符号说明：

C：每日所需总车次数； $C_{ij}$ ：上行或下行第j时段的车次；

$S_{ij}$ ：上行或下行第j时段平均发车时差； $P_{ij}$ ：上行或下行第j时段平均载客量；

$T_{ij}$ ：上行或下行的平均发车时间间隔； $M_{gi}$ ：上行或下行时公交公司日平均满意度；

$M_{ci}$ ：上行或下行时乘客整体日平均满意度； $M_{gij}$ ：上行或下行时公交公司各时段的满意度；

$M_{cij}$ ：上行或下行时乘客各时段的满意度；Q：每日所需车辆数；

B：满载率上限；b：乘客候车的时间；

$d_m^{+}$ ：为正偏差变量； $d_m^{-}$ ：负偏差变量； $w_k$ ：权重。

注： $i=1$ (表示上行运动， $k=1,2,3,\cdots ,14$ )。

$i=2$ (表示下行运动， $k=1,2,3,\cdots ,13$， $j=1,2,3,\cdots ,12$ )。

2.1. 最大客运量模型

本文把上行方向和下行方向的数据分成12个时段来处理，根据一天两个方向的每个站点上下车的乘客数量统计，要使公交车能够载完相同时间内到达的乘客，则必须载完各个时段乘客人数的最大值。我们便可以得到上行和下行这两个时间段时段内的最大客容量，如表1所示：

Table 1. Up and down each moment of maximum passenger capacity

表1. 上行、下行各个时刻最大客容量

2.2. 公交车调度最小车辆数问题

在本模型中，我们建立目标函数：

$\min Z=w_1{d}_1+w_2{d}_2+w_3{d}_3+w_4{d}_4$

$\{\begin{array}{l}x+d_1^{-}-d_1^{+}=b\\ x+d_2^{-}-d_2^{+}=1\\ f_i\left(x\right)+d_3^{-}-d_3^{+}=120,\left(i=1,2,\cdots ,13\right)\\ f_j\left(x\right)+d_3^{-}-d_3^{+}=50,\left(j=1,2,\cdots ,13\right)\\ d_m^{-},d_m^{+}\ge 0,\left(m=1,2,3,4\right)\end{array}$

关于对模型的求解，我们可求得公交车站的最小车辆数为13辆。其中上行方向的发车的时间间隔为x = 5.4分，上行车辆需求量为5.7辆；而下行方向的发车时间间隔为x = 6.1分，下行方向车辆需求量为6辆。此模型构建较为简单方便，求解过程简单容易，并且能综合地考虑公交车公司运营和乘客各方的切身利益。

2.3. 乘客满意度模型

现有的很多公交车调度模型虽然具有一定的优点，但基本都存在一个缺点：不能合理的描述乘客的满意度。乘客在乘车时候，乘客满意度主要取决于等待时间与车辆拥挤的程度。乘客的满意度会随着等待时间的增加或车中人数的增加而降低。当我们在刚到达公交站点时就可以上车，此时我们一定是非常开心的；当然，如果在等待较短一段时间内上车，也相对比较开心；但是，如果在等待一个小时后，车还没有来，人之常情，我们就会非常不耐烦了。也就是说，当乘客的等待时长超过一定的限度，并且时长逐渐增加时，乘客会越来越急躁，并且急躁的程度出现非线性增长。因此，只通过乘客的平均等待时间是与实际不相符的，类似来看，只用车中人数多少来刻画乘客的满意度也是不合理的。所以，我们需要两个递减函数来分别呈现乘客等车和乘车时的满意度分别随着等车时间和车中人数的变化，并称这种函数为满意度函数。我们把两者的综合满意度作为目标函数来构造出公交车调度的优化模型。

2.3.1. 刻画乘客满意度的依据

从乘客这一群体的角度出发，乘客如果长时间等车或者上车时人员过于拥挤都会让乘客产生抱怨甚至还会引起投诉。因此，我们需要尽最大的可能来提高乘客的候车满意度和乘车满意度。

2.3.2. 乘客等待时间的影响

当第i辆车到j站时，我们假设在第j站点上已在等候h辆车的乘客数量是

$W_{i,j}\left(h\right),h=1,2,\cdots ,h_{i,j}$

乘客已经等待车辆的时长是

$T{W}_{i,j}\left(h\right)=T_{i,j}-T_{i-h,j},h=1,2,\cdots ,h_{i,j}$

可将高峰时间段用集合Ʌ表示。

如果一个乘客到达车站之后只需等待很短一段时间后就能上车，那么他就会相对来说比较满意。相反，当他等待时间超过 $T^m$，他内心就会开始感到不太满意，如果这个时候等车时间依然不断增加，乘客则会产生烦躁甚至还会变得越来越不耐烦，乘客的烦躁程度会有一个大致的变化趋势。通常情况下会随等待车辆时间的增加而呈现出非线性的增长，有时甚至会是指数增长。基于这种现象，为了更好的刻画高峰时间段内乘客等待时间和候车满意度之间的关系，我们用单调递减凹效用函数 ${\mu }_1(·)$ 来刻画如图1所示。

Figure 1. The utility function of passenger waiting satisfaction

图1. 乘客候车满意度效用函数

因此，高峰的时段候车乘客总满意度可由如下式子决定

$P_1\left(T\right)=\underset{T_{i,j}\in \Lambda }{{\displaystyle \sum }}\left\{{\mu }_1\left(W_{i,j}\left(h\right)\right)\right\}=\underset{T_{i,j}\in \Lambda }{{\displaystyle \sum }}\left\{{\mu }_1\left(T_{i,j}-T_{i-h,j}\right)\right\}$

同理，我们要想更好的刻画高峰时间段内乘客等待时间和候车满意度之间的关系，可再次利用 ${\mu }_2(·)$ 这个递减凹效函数。 ${\mu }_2(·)$ 与 ${\mu }_1(·)$ 仅存的不同之处在于满意程度迅速下滑的临界点的时间变为了 $T^{mm}$，并且相对来说，下降的程度也比较缓慢。具体来说，非高峰时间段乘客候车总满意度由如下公式确定

$P_2\left(T\right)=\underset{T_{i,j}\notin \Lambda }{{\displaystyle \sum }}\left\{{\mu }_1\left(W_{i,j}\left(h\right)\right)\right\}=\underset{T_{i,j}\notin \Lambda }{{\displaystyle \sum }}\left\{{\mu }_1\left(T_{i,j}-T_{i-h,j}\right)\right\}$

为更清晰的说明问题，我们给出其中的一种具体情况为例进行分析，即，

${\mu }_1\left(x\right)=\{\begin{array}{l}1-\frac{x}{T^m},0\le x\le T^m,\\ -a_1{\left(x-T^m\right)}^2,x>T^m,\end{array}$

和

${\mu }_2(x)=\{\begin{array}{l}1-\frac{x}{T^{mm}},0\le x\le T^{mm},\\ -a_2{\left(x-T^{mm}\right)}^2,x>T^{mm}.\end{array}$

当 $0\le x\le T^m\left(T^{mm}\right)$ 时， ${\mu }_1\left(x\right)\left({\mu }_2\left(x\right)\right)$ 线性递减；当 $x=T^m\left(T^{mm}\right)$ 时， ${\mu }_1\left(x\right)=0\left({\mu }_2\left(x\right)=0\right)$ ；当 $x>T^m\left(T^{mm}\right)$ 时， ${\mu }_1\left(x\right)\left({\mu }_2\left(x\right)\right)$ 二次递减。当然这里 $a_1>a_2$，也就是说当乘客的等车时间超过了心理的预期之后，随着等待时间的越来越长，高峰时段相比于非高峰时段，乘客满意度下滑速度更迅速。

2.3.3. 刻画拥挤度的影响

当我们乘车时，如果人数比较少，那么每人都有座位，此时的乘客满意度是较高的；若人数逐渐超过座位数时，乘客就会觉得不舒心，那么满意度就开始下降；当人数超过了公交车规定载客量时，车内会变得拥挤，此时乘客满意度会急剧下降。因此我们用递减的凹效用函数 ${\mu }_3(·)$ 来反映乘客满意度和车内人数它们之间的关系。

${\mu }_2\left(x\right)=\{\begin{array}{l}1,x\le M,\\ -ax+c,M<x\le b,\\ -{\text{e}}^{x-a}+B,x>b.\end{array}$

其中M是公交车上的座位数.当 $x\le M$ 时，我们能够得到所有乘客都会有座位，此时，乘客的满意度可以达到最高(也就是100%)；当 $M<x\le b$ 时，公交车还没有到达正常载客量，这就会使乘客的乘车满意随乘客人数的增加发生变化且以线性递减；当 $x>b$ 时，当人数超过了公交车标准载客量时，人们会感到拥挤，非常不适应，这时会使乘客满意度随乘车人数的增加成指数下降，这个典型的乘车满意度效用函数，如下图2所示。

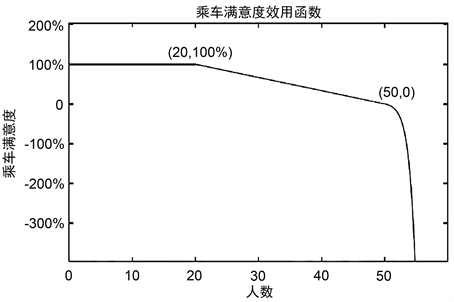
Figure 2. The utility function of ride satisfaction

图2. 乘车满意度效用函数

总之，乘车总满意度由下式来确定：

$Q\left(T\right)=\underset{i,j}{{\displaystyle \sum }}\left\{{\mu }_3\left(X_{i,j}\right)\right\}$

2.3.4. 乘客满意度综合模型的建立

根据我们上面的分析，我们一共有三个影响满意度的因素，

${\displaystyle {\sum }_{T_{i,j}\in \Lambda }\left\{{\mu }_1\left(W_{i,j}\left(h\right)\right)\right\}}$， ${\displaystyle {\sum }_{T_{i,j}\notin \Lambda }\left\{{\mu }_1\left(W_{i,j}\left(h\right)\right)\right\}}$ 和 ${\displaystyle {\sum }_{i,j}\left\{{\mu }_3\left(X_{i,j}\right)\right\}}$

如果想要使最终结果最优化，那么需要将这三个目标均最优化。此时，自然而然我们就会得到一个将多目标问题进行优化的难题。但是，多目标优化的问题不易求解。所以，这时我们通过加入三个正加权因子 $k_1,k_2,k_3$，总满意指标是使三个指标加权求和得出，下一步将总满意指标极大化求解，所以得出以下公交车调度优化模型：

$\max k_1\underset{T_{i,j}\in \Lambda }{{\displaystyle \sum }}\left\{{\mu }_1\left(W_{i,j}\left(h\right)\right)\right\}+k_2\underset{T_{i,j}\notin \Lambda }{{\displaystyle \sum }}\left\{{\mu }_1\left(W_{i,j}\left(h\right)\right)\right\}+k_3\underset{i,j}{{\displaystyle \sum }}\left\{{\mu }_3\left(X_{i,j}\right)\right\}$

3. 优化模型进行求解的算法

以上叙述所得出的模型是一个混合的整数规划问题，所以这是一个非线性规模较大并且具有较高的耦合程度的问题。这类问题的优化求解，我们可以借助一些已经得出的优化算法和软件。比如使用CPLEX，ILOG进行求解。CPLEX具有非常高的性能，能够非常稳定并迅速地求解线性规划问题二次规划、二次规划问题、混合的整数问题等等 [12]。因为CPLEX运算速度之快，能够解决我们现实生活中非常多的大规模规划问题，比如能够求解具有超百万个约束或者变量的有关问题。不过，为了更进一步提高CPLEX的求解速度，扩大求解规模，我们可以寻找一些更具有针对性的求解和计算方法。

4. 总结

文章所构建的模型给出了较优的调度方案，不仅需要考虑乘客的利益，还需要考虑公司的利益。并利用一些较为成熟的定理结论来对曲阜市现行的电动车公交路线进行评价，并以此给出改进方案。这个调度的方案能够方便地推广到m个时间段与n个车站站点 [13] 多个行驶方向的多方面调度方案问题，并且能够较好地评价衡量乘客和公司两者的利益的满意度。当然，以后的研究可以再考虑一下公交车在每一站的停车时间与乘客在上车、下车时的所用时间等。在有条件的情况下，为了避免意外因素造成的影响，可以增加必要的备用车。另一方面可以考虑仿真试验模拟电动公交车的运行方案，以求得到更好的调度并与理论模型结果进行对比分析。

基金项目

济宁学院国家级大学生研究性学习与创新性实验计划资助项目：201810454010。

NOTES

^*通讯作者。