1. 引言
水电作为我国能源体系中重要的组成部分,在国家能源供给方面承担着不可替代的作用。梯级水电站的统筹优化调度,能充分发挥水电站整体经济效益,是节约水电能源的重要方法。然而,随着梯级调度工作的不断深入,对优化模型的建立和求解都提出了更高的要求 [1]。其中,短期优化调度因其复杂的约束条件,日益精细化和实用化的需求,以及求解精度和效率的限制,已成为水电站群优化调度的重点和难点问题 [2] [3] [4] [5]。
短期优化调度主要有两种模式 [6]:“以水定电”和“以电定水”。前者是给定各水库末水位,在计划期内依照调度目标调节水量时空分布。后者是给定各时段水电系统负荷需求,在各电站间分配出力。主要采用期末蓄能最大模型,该模式制定的调度计划直接涉及到各电站和各机组负荷分配情况,直接影响梯级水电站的安全、稳定、经济运行情况,因此提升该模型求解的有效性对实际的调度意义重大。
目前对于期末蓄能最大模型常用的求解方法是拉格朗日松弛算法 [7],而梯级水电站规模庞大,上下游水力电力联系密切且复杂,约束条件较多且繁琐,因此使用该求解算法易造成耗时多,求解精度低等问题。同时短期调度时段划分较细,使得拉格朗日乘子向量规模较大,需进行多次向量更新,极大地限制了计算效率。无法满足短期调度的时效性和结果的实用性。
本文为解决上述问题,对期末蓄能最大模型中的总负荷需求约束进行了等价转换,并采用凝聚函数方法 [8] 进行了简化,并建立只有一个乘子的对偶优化问题。然后采用次梯度法和逐次逼近法实现对该优化问题的求解。以乌江梯级电站为实例,求解各电站出力过程验证了所提方法的有效性。
2. 模型描述
2.1. 目标函数
在“以电定水”的模式下选取期末蓄能最大为目标函数,其表达式如下:
(1)
式中:F为梯级水电站总的期末蓄能;m为参与调度电站编号,M为水电站群参与调度的电站总数(
);
为电站m及其上游所有电站死水位以上蓄水量可产生的电量,如式(2);
为电站m上游所有电站在电站m产生的滞时电量,如式(4)。
(2)
(3)
式中:t为调度时段,T为调度时段总数,调度期内
;
为水库m在T时段初的库容;
为电站m的平均耗水率;
为水库m及其上游所有水库在调度期末死水位以上的蓄水量;
为电站m的直接上游电站编号数组;k为直接上游电站编号,
为电站m的直接上游电站总数目(
);
为第k个直接上游水库在T时段初的库容。
为所有第k个直接上游水库在调度期末死水位以上的蓄水量。
(4)
(5)
式中:
为水库m上游所有水库的滞时水量;
,
为有滞时关系的上游
号电站和下游电站m间的最大及最小滞时时段数;
为第t时段的小时数;
为上游
号电站在n时段出库流量为
时,在下游m号电站
时段以后产生的入库水量,如式(6)
(6)
式中:
为上游
号电站水库出库流量为
时的滞时时段数。
2.2. 约束条件
1) 水量平衡约束
(7)
(8)
(9)
式中:
是电站m在t时段末的库容;
是电站m在t时段末的出库流量,
,
,
分别是电站m在t时段末的发电流量,弃水流量;
为电站m在t时段的入库流量,
为电站m在t时段的区间入库流量,对于龙头电站则为总入库流量;用函数
计算电站m的第k个有滞时关系的上游电站各时段出库流量在时段t流至电站m的总量。
2) 发电流量约束
(10)
式中:
,
为电站m在时段t的发电流量及其最大发电流量。
3) 水电站出力约束
(11)
式中:
,
,
为电站m在时段t的出力及其上下限。
4) 库水位约束
(12)
式中:
,
, 为电站m在时段t的初水位及其上下限
为电站m在时段t的初水位及其上下限
5) 出库流量限制
(13)
式中:
,
为电站m在时段t的出库流量及其上下限
6) 水电站出力爬坡约束
(14)
式中:
为电站m在相邻时段的最大出力升降限制。
7) 水电站出力波动限制约束
(15)
式中:
是电站m出力升降最小间隔时段数,即在一轮出力升降过程最高最低点需持续最少
个时段。
8) 最小出力升降时段数限制
m出力上升开始至下降开始,或由下降开始至上升开始的时间间隔不少于
个时段
9) 水电站总负荷约束
(16)
式中:
为第t时段的系统梯级总负荷。
3. 求解方法
期末蓄能最大模型是求解梯级水电站短期负荷分配优化问题常用的模型,这一类问题是具有强系统性约束的非线性优化问题,常利用拉格朗日松弛法进行求解,它通过引入拉格朗日乘子将具有复杂约束的原优化问题,转化为不包括强约束的松弛问题。其建立的对偶优化问题如下:
(17)
式中:F为优化问题的目标函数期末蓄能值,
为t时段拉格朗日乘子向量分量。
是各电站各时段的出力集合,
拉格朗日乘子向量集合。
该对偶问题是由两部分优化问题组成,外层是以拉格朗日乘子B为决策变量的优化问题,内层是以各电站的出力A为决策变量的优化问题。因此,除原问题需要求解的决策变量外,还多出了新的需要求解的变量集合B。求解中需要对B中的拉格朗日乘子进行多次迭代更新:
,其中
和
为乘子
在第i + 1和i轮次迭代的取值,
为乘子更新步长,可随迭代轮次逐步减小。每个时段均对应一个拉格朗日乘子,所以该对偶问题共含有T个乘子。由于短期优化调度对时段的划分较细,使得该集合包含的乘子数量较多,加大了求解困难,明显降低求解效率,影响求解质量。如在以15分钟为计算时段时,日调度计划的优化需要迭代确定96个乘子的取值,所以为实现对偶问题的简化,对求解方法进行了适当的改进,使其能有效降低拉格朗日乘子个数,提升求解效率。
为此,本文提出一种简化方法。约束条件式(16)等价于
,对于T个负荷平衡约束,每个时段一个的约束式
等价于
,
。因此,可使 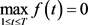 替换约束条件(16)。
替换约束条件(16)。
由于最大值形式的约束条件在求解中难以处理,可进一步采用凝聚函数法将
近似转化为式(18)。
(18)
其中p为控制参数,取值为0.01。
经上述变换后,建立新的对偶问题,其目标函数为式(19):
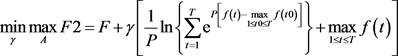 (19)
(19)
式中:
为拉格朗日乘子。
对比式(17)和(19)可明显看出,拉个朗日乘子由含有T个乘子的集合B变为单个乘子
,大大地减少了需求解的变量个数,简化了迭代流程,能有效的降低求解复杂度,提升求解效率。
需要说明的是,无论原问题还是简化后的问题,都不能完全满足拉格朗日松弛法的收敛条件,计算结果存在对偶间隙,表现为电站出力和总负荷的不平衡,需要在求解后进行电站出力的进一步调整。
优化求解流程
求解利用拉格朗日松弛法所构造的对偶问题时,关键点在于拉格朗日乘子的更新迭代。常采用次梯度法,该方法是沿次梯度的方向搜索,找到函数的极值点。本文采用逐次逼近法和次梯度法进行对偶问题的求解和乘子的更新。简化问题的计算流程如下(图1):
1) 初始化拉格朗日乘子
,
;
2) 采用逐次逼近的算法求解2中所建立的数学模型,目标函数此时
;
3) 采用次梯度法更新乘子,即
, 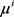 为乘子更新步长,设
;
为乘子更新步长,设
;
4) 收敛判断:
,
为收敛精度;或
,
也为收敛精度,代表总负荷约束误差和的微小变化值;又或
,设终止迭代次数I。满足收敛条件,结束整个迭代流程,否则转步骤(2)。

Figure 1. Simplified method solution flowchart
图1. 简化方法求解流程图
在使用逐次逼近算法对问题进行求解时,要考虑模型未被松弛的其它约束,其中发电流量上限、水电站出力上限、库水位、水量平衡等约束通过单时段以水定电计算满足,电站出力下限和出库下限约束可采用惩罚函数处理,惩罚项为
,其中a、b为惩罚系数。本文重点对模型中与电站出力升降相关的3个时间耦合型约束进行处理。为便于3个约束的处理,减小计算量,将其转化为以发电流量表示的约束,并采取合适的方式修正调整以满足约束条件,具体方法如下:
1) 为满足电站出力波动限制约束,在初始解的基础上(如图2(a)),调整发电流量(如图2(b))。在t时段发电流量由
变成
,向前扩展时段
,
,
的出力,向后扩展时段
,
,
的出力,使其满足约束
。
2) 为满足出力爬坡约束,在上述调整时段的边缘对出力变化幅度进行修正(如图2(c))。在上一步扩展调整后,扩展的范围为
。首先向t1以前寻找最大的时段t0,使其满足
,(
),再顺次依照爬坡出力值调整
,
,
,
的发电流量;然后向t2以后寻找最小的时段t3,使其满足
,(
),再顺次依照爬坡出力值调整 ,
,
,
的发电流量。
,
,
,
的发电流量。
3) 为满足出力升降时段数约束,在上两步的基础上,对发电流量变化范围的两侧进行检验和修正(如图2(d))。在经过上述调整后,发电流量范围为
。首先向t0以前寻找最大的时段t4,其能满足
,若
,则通过检验;否则在t0后和t4前继续寻找t5,t6使
,
,
完成前半部分的流量修正。t3以后的修正方法同上。
4) 为满足出力升降时段数约束,对发电流量继续进行修正(如图2(e))。在此阶段发电流量范围为
,t7为上一步由t3时段向后修正时得到的最大时段号。首先向t5以前寻找最大的时段t8,其能满足
,(
)若
,则继续搜索距离最大的t9,使得
,(
)修正后
间满足约束要求,完成前半部分修正。t7以后的修正方法同上。
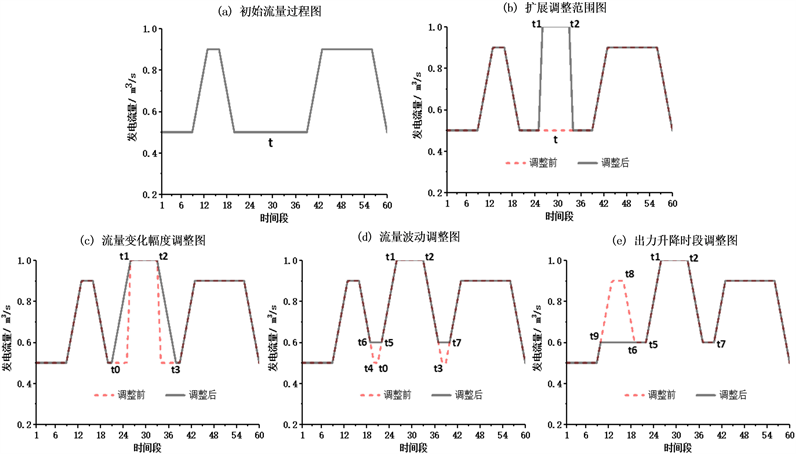
Figure 2. Correction and adjustment diagram
图2. 修正调整示意图
4. 应用实例
4.1. 工程背景
我国十三大水电基地之一的乌江流域水力资源得天独厚,目前规划的梯级水库已全部建成,这些水库调节性能多样,联合调度方式较复杂,加大了对短期期末蓄能最大模型的求解难度。为验证方法的可行性,本文以乌江梯级其中的8座电站为例,结合实际的运行情况,采用本文叙述的理论方法进行计算并对所求结果进行分析。各水库的基本参数如表1所示。乌江水电系统结构如图3所示。

Table 1. Basic parameters of the reservoirs
表1. 各水库基本参数
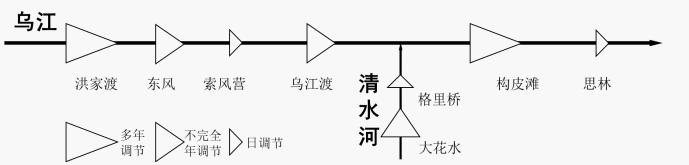
Figure 3. Schematic layout of studied hydropower system
图3. 乌江水电系统结构图
4.2. 计算结果及分析
选取各电站某一日来水数据和该日系统总负荷数据,调度期为1日,时段为96个,分别采用问题简化前后的式(17)和(19)为目标函数对模型进行求解。
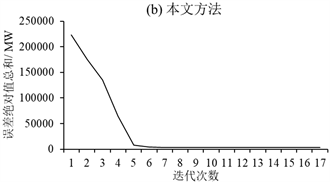
Figure 4. Comparison chart of the sum of absolute errors
图4. 误差绝对值总和对比图

Figure 5. Comparison chart of objective function
图5. 目标函数值对比图
图4是两种方法的误差绝对值总和对比图,表示各时段系统出力与给定负荷之差的绝对值的总和。图5是两种方法目标函数值的对比图。原方法在迭代100次时误差总和为19,672 MW,继续进行迭代计算改进幅度很小。由于各时段乘子相互影响,同时因为存在电站出力平稳性约束,使得图4(a)中误差绝对值总和在下降过程中出现反复跳动,且下降速度缓慢。同样,图5(a)中目标函数在计算过程后期也存在反复跳动现象。说明原方法求解效率较低,主要由于本模型中采用了电站出力平稳性等时段关联约束,使得求解多个时段的拉格朗日乘子更加困难。而采用本文方法在迭代17次后误差值绝对值之和为2963 MW,明显小于原方法。同时本文方法中,误差和目标函数的变化都比较快,实际上在5轮次迭代后便接近最终求解值,说明本文方法收敛迅速。由于两种方法在梯级总负荷约束条件的满足程度不同,因而最终目标函数的比较意义不大。
图6为求解得到的乌江梯级各电站的出力过程,从图中可以看出各电站均在出力的上下限范围内波动,满足电站出力约束。观察各电站的出力升降情况,相邻两个时段的最大出力升降满足限制要求,电站在某一出力持续运行的时段数、升降开始的时段数均符合要求。洪家渡作为该流域的龙头电站,具有多年调节性能,整个时段出力过程较平稳,机组保持满发,但在两个负荷高峰的时段,电站的出力有微小下降,主要由于其他电站出力平稳性、升降时段等约束限制了它们在相应时段的出力调节的灵活性,因而一些微小、频繁的出力波动由洪家渡承担。东风和乌江渡是两个不完全年调节的电站,两个电站的出力过程和整个系统的负荷过程基本吻合,深夜保持平稳的出力运行,负荷高峰时电站出力上升,负荷低谷时电站出力下降。索风营和思林为系统中的日调节电站,其余时段不发电,在系统负荷高峰时开机发电。构皮滩作为整个梯级中段部分的一个控制性电站,受下游思林运行的影响,其出力过程也与系统负荷过程一致。大花水和格里桥电站整个计算期不发电,主要由于本例中支流龙头电站大花水库水位较低,在其他电站能够满足梯级负荷的条件下,这两个电站停机蓄水有利于提高期末蓄能。该结果较合理的反映了梯级水电站之间负荷分配,在保证了系统出力基础上,也使系统的蓄能最大,极大化地利用了梯级的水能资源。


Figure 6. Output power process of each power station
图7中的曲线分别代表优化求解得到的电站出力总过程和事先给定的系统负荷需求,两条曲线几乎完全重合,说明该优化问题的结果能完全满足总负荷约束的要求,保证了系统的安全运行,符合实际的生产需要。综上,求解该模型时所采用的简化方法能得到合理且实用的优化结果,能有效地求解以期末蓄能为目标的实际工程问题。
5. 结语
随着我国水电事业的发展,对梯级水电站短期优化调度的要求也更加精细和深入,使相关模型的规模愈加庞大繁琐,求解愈加困难。对于期末蓄能最大模型的求解就是其中的典型,该模型常使用拉格朗日松弛算法进行求解,而该方法涉及到乘子的更新迭代,加剧了求解的复杂性。本文针对因乘子向量规模巨大造成求解困难的问题,提出了一种简化的方法。该方法将多时段总出力约束替换为一个约束,并利用凝聚函数法对该约束进行近似的转换,从而把包含多个乘子的对偶优化问题转换为仅含一乘子的问题。采用次梯度法和逐次逼近法求解该对偶问题。通过乌江梯级电站的实例分析表明,所提的方法能明显减少乘子的数量,有效地简化问题求解,在得到实用合理结果的同时提高了求解效率,对求解梯级水电站优化调度涉及乘子的相关问题具有借鉴和参考价值。
基金项目
国家重点研发计划(2016YFC0402208);国家自然科学基金(51679027, 91647113)。