1. 绪论
2019年12月底,新型冠状病毒肺炎疫情悄然而至,其波及范围之广,给海内外同胞造成重大影响。在国内,武汉地区首当其冲。自2019年底陆续有病例呈报,其发展态势不断升级。2020年1月22日,湖北省启动突发公共卫生事件II级应急响应。1月23日10时起,武汉市公交,地铁等交通设施暂停运营。1月24日,湖北省启动I级响应,各地医护人员驰援武汉,火神山医院开始投入建设。2月12日起,湖北省确诊标准发生变化,临床诊断被纳入确诊。截止4月7日,武汉市累计报告新冠肺炎确诊病例50,008例,累计出院46,991例,累计病亡2572例。次日4月8日起,离汉离鄂通道管控解除。
在本次疫情中,武汉是国内重灾区,也是一座英雄的城市,它在承载着巨大负荷的同时,用抗争与勇气见证了武汉乃至全国对疫情发展态势的逐步控制。正是上至国家政府的宏观政策,下至社区家庭的微观管理,武汉才得以顶住压力进而重焕生机。尽管目前国内疫情发展基本态势已定,但对武汉地区疫情发展过程中关于病毒特性、隔离及救治能力等方面的研究仍旧意义重大。这不仅是对突发公共卫生事件应急处理的总结,更对今后传染病防控与公共卫生安全政策制定大有裨益。
在这段时间内,疫情在全球多国多点暴发。病毒不分国界,但新冠疫情在不同国家和地区的发展态势却大不相同,究其原因,是因为现实情形复杂多变,各受不同因素和环境的制约。武汉是中国的典型代表,它以严密的防控防治举措有效应对疫情,积极为全球输送抗疫经验。不可否认,抗疫过程中人为干预与隔离措施至关重要。同样,对于不足之处的探讨能为未来的传染病防控提供经验借鉴。因此,对武汉地区COVID-19疫情进行研究与分析就显得尤为重要。
疫情暴发以来,国内外大量科研工作者积极投身流行病学研究,取得一系列有启发意义的成果。严阅等人 [1] 提出一类基于时滞动力学系统的传染病动力学模型,通过引入时滞过程,贴切地刻画出潜伏期与治疗周期对疫情发展的影响。Joseph T Wu等人 [2] 利用官方航空指南的每月航班预订数据及腾讯数据库人口流动数据,由武汉传播到国际上的病例数推断出武汉病例数及武汉传播到中国其他城市的病例数。此类基于传统SEIR传染病模型的研究,根据新冠病毒传播特性对模型进行不同创新,从不同角度贴近现实。
传统SEIR传染病模型 [3] 仅仅将人群划分为易感者、潜伏者、感染者与移出者,且其中潜伏者不具备传染能力,然而这并不符合新冠病毒的传播特性。此外,武汉地区疫情严重时涌现大量重症和危重症患者,一度出现“一床难求”的危急局面。而后,大量医务工作者驰援武汉及大量医疗资源的陆续供应,才使得医院逐步“应收尽收”。因此,传统SEIR模型并不能直接用于刻画武汉疫情,需要经一定修正后进行研究。
本文以武汉疫情为研究对象,修正传统SEIR传染病模型,考虑潜伏者也具备传染能力,在传染动力系统中加入重症感染者并将传统SEIR传染病模型中的移出者细分为治愈者和病亡者,建立符合新冠病毒传播特性及武汉疫情特点的SEIHCD模型。
本文还重点考虑传染病模型参数非常数这一事实,根据疫情发展关键节点将武汉疫情分为三阶段,分别反演出各阶段模型参数。代入所估参数,求解传染动力系统常微分方程组,对比模拟数据与通报数据。对表征隔离力度的模型参数进行扰动分析,分析隔离力度对疫情发展的影响。得到三阶段治愈率、死亡率等数值结果。分析各阶段模型参数,回顾和总结本次武汉新冠疫情。
2. 数据来源与假设
2.1. 数据来源与说明
2020年1月10日至2020年1月19日武汉地区COVID-19疫情累计确诊人数、死亡人数及治愈人数来源于中华人民共和国国家卫生健康委员会 [4]。此后日期的数据来源于湖北省卫生健康委员会 [5] 和中华人民共和国国家卫生健康委员会。通报数据中只包含研究时间阶段内完整的累计确诊人数以及部分死亡人数与治愈人数。
2.2. 基本假设
在武汉地区传染动力系统中,总人群分为易感者、潜伏者、普通感染者、重症感染者、治愈者和病亡者;由新冠病毒传播特性,处于潜伏期的潜伏者也具有传染能力,重症感染者因重点隔离故不考虑其传染能力;潜伏者以某一单位时间概率转化为普通感染者,这一概率在数学意义上表示潜伏期时长的倒数;假设单位时间内一个具有传染能力的人所接触人数为定量,称之为接触率;假设病毒传染给易感者使其成为潜伏者的概率为一常数;潜伏者必将经历转为普通感染者这一阶段;感染者有一定概率被治愈,普通感染者可能直接被治愈或转为重症感染者,重症感染者会转为普通感染者或不幸病亡。
3. 模型建立
3.1. 三阶段建模
疫情刚开始蔓延时,大多数病人处于潜伏期并未出现显著症状,但感染人数呈爆发式增长;自武汉封城至湖北换帅,武汉及其周边城市陆续封城,火神山医院和雷神山医院陆续交付使用;湖北换帅至武汉解封,新冠病毒特免血浆制品在湖北投入临床治疗,武汉交通管控升级进一步升级,病人从“一床难求”到“应收尽收”。
根据上述对疫情关键事件的分析,将疫情发展分为三阶段,为潜伏蔓延期、封城暴发期和攀升消退期 [6]。第一阶段为2020年1月10日至2020年1月22日,第二阶段为1月23日至2月12日,第三阶段2月13日至4月7日。
3.2. 建立SEIHCD传染病模型
基于传统SEIR模型,结合新冠病毒传播特性,考虑潜伏者也具备传染能力。同时,因潜伏者和感染者携带病毒的程度可能不同,就这两个群体对易感者的感染能力进行区分,即分别设置模型中表征传染的参数。此外,将感染者细分为普通感染者和重症感染者,将移出者细分为治愈者和病亡者。传染动力系统见图1。
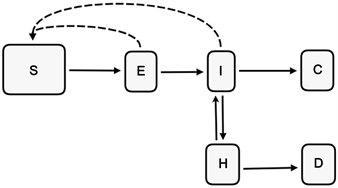
Figure 1. Infectious power system of COVID-19
图1. COVID-19传染动力系统图
基于上述假设及分析,建立易感–潜伏–普通感染–重症感染–治愈–病亡(SEIHCD)模型:
(1)
(2)
(3)
(4)
(5)
3.3. 模型解释
和
分别表示易感者,潜伏者,普通感染者,重症感染者,治愈者和死亡者数量,由于这六大群体之间没有重复交叉,则在该传染动力系统中,这六个数量之和为武汉总人口数N,即
(6)
(1)式左边表示易感者人数的变化,右边表示易感者分别受到潜伏者及普通感染者的感染而减少。
分别表示潜伏者和普通感染者的接触率,由于重症感染者集中救治且严格防护,故假设其接触率为0。
为病毒传染给易感者使其成为潜伏者的概率。
(2)式左边表示潜伏者人数的变化,潜伏者的增加来源于被感染的易感者,潜伏者的减少是由于转为普通感染者。因此右边两个正项代表受潜伏者和普通感染者感染后潜伏者的增加,负项代表潜伏者转为普通感染者。
代表潜伏者转化为普通感染者的单位时间概率。
(3)式左边表示普通感染者人数的变化,(3)式右边第一个正项来源于潜伏者,第二个正项来源于重症感染者的好转,另外两个负项表示普通感染者一部分转为重症感染者,另一部分则被治愈。
表示普通感染者转化为重症感染者的单位时间概率,
表示重症感染者转化为普通感染者的单位时间概率,
表示普通感染者转化为治愈者的单位时间概率。
(4)式左边表示重症感染者人数的变化,(4)式右边第一个正项表示部分普通感染者病情加重故重症感染者增加,另外两个负项表示重症感染者的减少,一部分以单位时间概率
转为普通感染者,另一部分以单位时间概率
死亡。
(5)式左边表示治愈者人数的增加,来源于普通感染者。
由于上述六个群体有(6)式的关系,故(7)式自动成立:
(7)
该式表示表示病亡者来源于重症感染者的不幸死亡。由于易感者、普通感染者、
重症感染者、治愈者和病亡者总和为该地区传染有效总人数,故在该传染动力系统中,常微分方程(7)在常微分方程组(1)~(5)满足时自动满足。
4. 模型求解
4.1. 数据预处理
由卫健委官网得2020年1月10日到2020年4月7日之间的累计确诊数、部分重症危重症数、累计治愈人数和累计死亡人数等信息。而通报数据中存在一定缺失,由于需确定所建模型常微分方程组初值,故首先进行数据预处理。
4.1.1. 缺失值H补齐
在本研究中,假设重症、危重症均纳入重症感染者(H)。首先绘出重症比例(H/(I + H))的时序图,见图2。利用对数回归对缺失数据进行补齐,然后根据各时段通报的感染者人数(普通感染者与重症感染者之和)及预测出的重症比例,反推各时段重症感染者人数。
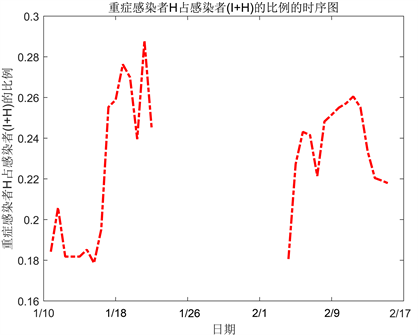
Figure 2. Severe proportion time series (including missing data)
图2. 重症比例时序图(含缺失)
为对重症感染者进行补全,利用线性回归对重症比例进行拟合和预测。由于该序列显然不是平稳的时间序列,本文对其取对数后再作线性回归。重症比例取对后的回归直线见图3,对数线性回归的残差序列图见图4。
4.1.2. 缺失值E补齐
新型冠状病毒肺炎的平均潜伏期为5.1天 [7],本文取平均潜伏期5天。由所建模型,易感者(S)受传染后首先变为潜伏者(E),潜伏者再转为普通感染者(I),普通感染者可能直接治愈移出到治愈者(C),或者转为重症感染者(H)。重症感染者或者因病情减轻而转化为普通感染者,或者因病情加重最终不幸移出到死亡者(D)。由潜伏期含义,其数量由下式推算可得:
(8)
分别表示时刻n的潜伏者,普通感染者,重症感染者,治愈者和病亡者的实时数量。由此,潜伏者的数量可以全部推算出。
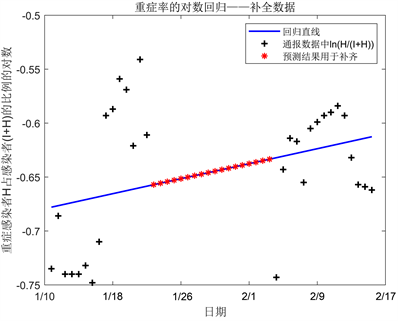
Figure 3. Log regression of severe proportion
图3. 重症率的对数回归
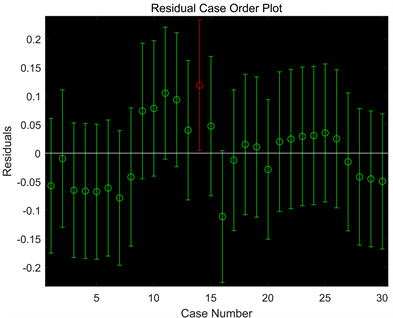
Figure 4. Residual time series of log regression based on severe proportion
图4. 重症率对数回归的残差序列图
4.1.3. 确定N的取值
在传统的SEIR模型中,N (见(6)式)表示传染地区忽略自然出生率及死亡率的总人口数。但在本研究中,N并不表示武汉地区的总人口数。由于传统SEIR模型假定各群体个体自由流动。实际上,由于防控隔离等政策,武汉总人口中可能接触到具备感染能力的人数是一定的,而并非全部人口 [8]。由参数估计结合经验测算,得该数值约为200万。
4.1.4. “换帅”骤跳修正
由卫健委通报数据,2020年2月12日当天通报数据显示武汉新增确诊病例13,436例,该数值较之前出现明显陡增。卫健委的解释为湖北省新增“临床诊断病例”分类,对疑似病例具有肺炎影像学特征者,也确定为临床诊断病例。不难判断,这些大量新增的临床诊断病例并非一天之内增加,其中累积了部分在诊断标准尚未变更之前的临床诊断病例。
为更贴切实际情况,需要修正陡增数据。由本文所建立模型,潜伏者必将转化为普通感染者,故本文对普通感染者数目进行修正。由于疫情初期感染者的数量呈指数上升,故本文采用指数函数对普通感染者的数量进行拟合,拟合函数如该式:
(9)
其中t从武汉封城2020年1月23日为第1天开始,通过对拟合函数取对数化成线性回归问题,再利用最小二乘法等方法估计参数。本文利用最小二乘法估计参数,通报情况及修正后图像见图5。通过对普通感染者数目进行修正,将累积临床诊断病例合理地回放到之前时间段,骤跳现象被明显改善。
经过以上处理,得到研究期间各群体每日数量。由于潜伏者S与其他群体数量级相差太大,其他群体经处理后的实时数量见图6。
4.2. 参数估计
4.2.1. 估计说明
设
,由公式(1)~(5)得
(10)
(11)
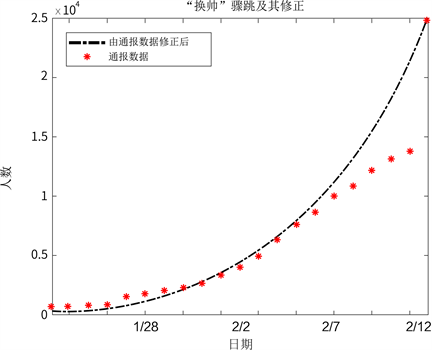
Figure 5. Surging data and its correction
图5. “换帅”骤跳及其修正
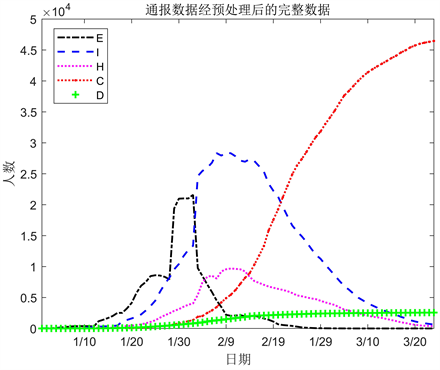
Figure 6. Complete data after processing
图6. 通报数据经预处理后的完整数据
由(10) (11)及(3) (4) (5)可知,待估参数为
。
分别反映了易感者受潜伏者和普通感染者传染的力度,与该传染动力系统有效总人口数、潜伏者和普通感染者的接触率有关。
反映了易感者一旦有效接触到新型冠状病毒(SARS-Cov-2)后感染的概率,由于该病毒传染性极强,本文设为0.99。
在数学含义上表示平均潜伏期的倒数,由 [7] 可知,新冠肺炎的平均潜伏期为5天,故
取为0.2。剩下四个参数
由参数反演得到。
4.2.2. 经验取值
由以上说明,参照相应文献或经验可得
的估计值,经验估值见表1。

Table 1. Empirical parameter estimate and its basis
表1. 参数估计的经验估值以及依据
4.2.3. 搜索估计
对上述4个参数进行经验估计后,还需要对参数
进行估计。由模型含义可知,这4个参数的取值范围在0到1之间。采用搜索算法 [10],取一定步长如0.1对参数进行遍历,得到4个参数的不同组合,将所有参数作为已知条件代入常微分方程组(8)~(12)利用Matlab进行数值求解,得到各群体实时模拟数量。以普通感染者数量的残差平方和最小化作为目标函数,得到
的最小二乘估计:
其中
表示普通感染者的模拟数量。
4.3. 估计结果
由湖北卫健委和国家卫健委通报的数据可以确定SEIHCD模型各群体部分初值,其余初值可通过上述的数据预处理得到。利用所估参数,代入所建传染动力系统常微分方程组,求解并绘出通报数据曲线图和利用所估参数模拟的曲线图 [11]。
4.3.1. 第一阶段潜伏蔓延期(2020/1/10~2020/1/22)
在第一阶段2020年1月10日到2020年1月22日期间,武汉地区尚未封城,新型冠状病毒肺炎疫情呈现潜伏蔓延的状态。初值条件即截止2020年1月10日的数据为:
。第一阶段具体参数估计见表2。

Table 2. Parameter estimation results of the first stage
表2. 第一阶段参数估计结果
将第一阶段的参数估计结果代入常微分方程组(8)~(12),由Matlab绘出潜伏蔓延期该动力系统中普通感染者的实时模拟数量的图像见图7,治愈者的实时模拟数量的图像见图8。
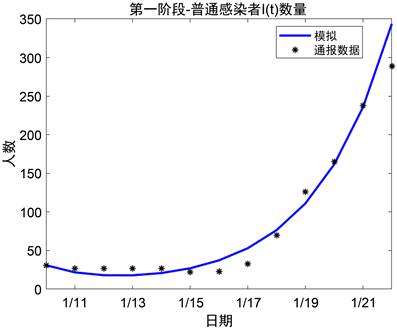
Figure 7. Comparison chart between reported data and simulation result of I at the first stage
图7. 第一阶段普通感染者通报人数曲线和模拟曲线

Figure 8. Comparison chart between reported data and simulation result of C at the first stage
图8. 第一阶段治愈者通报人数曲线和模拟曲线
由上述图像,第一阶段普通感染者数量大体呈指数上升趋势。由于在疫情暴发初期,易感者不断地被传染为潜伏者,进而转为普通感染者,而该时间段内治愈率又较低,故普通感染者人数呈指数上升。同时,由于初期对新冠病毒了解尚不深入,故治愈者人数的上升较为平缓。
4.3.2. 第二阶段封城暴发期(2020/1/23~2020/2/12)
考虑到2月12日诊断标准发生变化,采用对骤跳现象进行修正后的数据。初值条件即截止2020年1月23日的数据为:
。第二阶段具体参数估计结果见表3。

Table 3. Parameter estimation results of the second stage
表3. 第二阶段参数估计结果
将第一阶段的参数估计结果代入常微分方程组(8)~(12),由Matlab绘出封城暴发期该动力系统中普通感染者的实时模拟数量的图像见图9,治愈者的实时模拟数量的图像见图10。
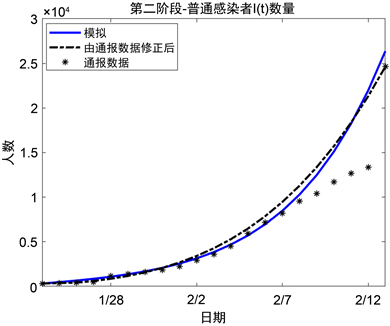
Figure 9. Comparison chart between reported data and simulation result of I at the second stage
图9. 第二阶段普通感染者通报人数曲线和模拟曲线
由图像可知,模拟曲线很好地拟合了由通报数据修正后的普通感染者人数。武汉封城后,普通感染者数目仍旧呈指数式攀升,但上升坡度相较于第一阶段有所放缓。一方面,疫情前线不断积累了预防、确诊与救治等经验,对普通感染者增加速度有所遏制。另一方面,在2020年1月23日至2020年2月12日期间,各级对疫情防控有更清醒认识,防控隔离措施更加严格。
4.3.3. 第三阶段攀升消退期(2020/2/13~2020/4/7)
由于2020年4月8日武汉解除离汉通道管控,故将此前一日作为本次研究第三阶段的结束时间节点。初值条件即截止2020年2月13日的数据为:
。第三阶段参数估计结果见表4。

Table 4. Parameter estimation results of the third stage
表4. 第三阶段参数估计结果
将第一阶段的参数估计结果代入常微分方程组(8)~(12),由Matlab绘出攀升消退期该动力系统中普通感染者的实时模拟数量的图像见图10,治愈者的实时模拟数量的图像见图11,治愈者的实时模拟数量的图像见图12。
由图像可知,第三阶段即2020年2月13日至2020年4月7日之间,普通感染者数量呈现先增加后减少的趋势,在2月下旬到达峰值。对于普通感染者,其来源是潜伏者转为确诊及重症感染者病情减轻转回为普通感染者。其去向也有两个方面,一是由于病情好转而转为治愈者,另一个是因症状加重而转为重症感染者。由于普通感染者的流出要大于流入,因此在峰值之后,普通感染者的数目不断减少。与此同时,治愈者的数量不断增多,截止4月7日,这一数值为46,991人。

Figure 10. Comparison chart between reported data and simulation result of C at the second stage
图10. 第二阶段治愈者通报人数曲线和模拟曲线
另外,当新发的疑似感染病例下降,确诊的发病患者数量下降时,可以认为新型冠状病毒肺炎发展的拐点特征出现。由图11可知,2020年2月19日附近出现了拐点,普通感染者的数量达到峰值,开始呈现下降的趋势。拐点判断可以帮助公共卫生政策的制定及病情救治方案的调整,对疫情整体防控有着重要作用。
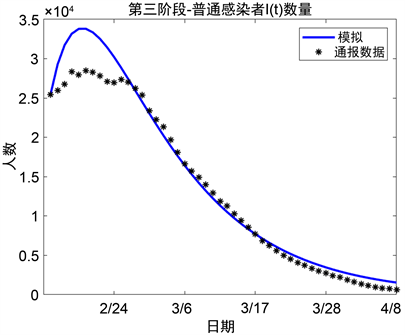
Figure 11. Comparison chart between reported data and simulation result of I at the third stage
图11. 第三阶段普通感染者通报人数曲线和模拟曲线
5. 结果与讨论
5.1. 防控力度对疫情规模的影响
根据模型求解结果,三阶段反演的表征隔离力度的参数对比见表5。

Table 5. Comparison of quarantine parameters of the three stages
表5. 三阶段隔离力度的参数对比
由所建模型,
和
分别表示潜伏者和普通感染者的接触率,N表示该传染动力系统的有效总人数。故
和
分别表示与潜伏者和普通感染者的接触率及有效总人口数有关的参数,可用这两个参数一窥不同阶段下武汉地区的防控隔离力度。
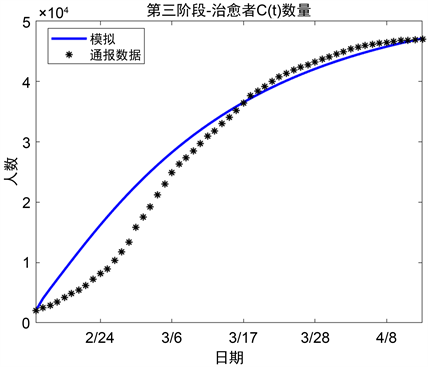
Figure 12. Comparison chart between reported data and simulation result of C at the third stage
图12. 第三阶段治愈者通报人数曲线和模拟曲线
首先,这两个参数随着时间增加都呈现一定减小趋势,这说明随着时间递增隔离力度逐渐加大,这也与实际情况相符合。其次,在第一、第二阶段中,表征潜伏者接触率的参数要大于普通感染者接触率的参数。这是由于潜伏者由于尚未表现出显著症状未被确诊,所以其自由活动的空间更大,容易感染更多的易感者。而普通感染者由于已经确诊,其接触人数只会是其相关的医护人员。
5.2. 救治水平的分析
根据模型求解的结果,三阶段反演的与救治水平有关的参数的对比见表6。

Table 6. Comparison of curing parameters of the three stages
表6. 三阶段救治水平的参数对比
由上表可知,
和
表征患上新冠肺炎后病情加重的程度。从第一阶段到第三阶段,普通感染者转为重症感染者的单位时间概率先增加、后减少。疫情初期由于对该传染病了解不深,预防与救治方向不够精准,故普通感染者转重症感染者呈上升趋势。然而,当疫情发展到一定阶段,经科研人员与医务工作者的不懈研究,加上医疗队伍的壮大与医疗设备的完善,普通感染者转化为重症感染者的单位时间概率显著降低。
相应地,
和
表征患上新冠肺炎后病情减轻的程度。可见,三阶段下这两个参数呈单调下降趋势,说明在广大医务工作者的共同努力下,武汉地区医疗救治水平得到显著提升。治愈率与死亡率时序图见图13。

Figure 13. Cure rate and death rate time series
图13. 治愈率与死亡率时序图
5.3. COVID-19疫情阈值分析
由图11可知,2020年2月19日附近,第三阶段的普通感染者人数达到峰值,结合图6可知,这也是整个疫情阶段普通感染者人数的峰值。设该传染动力系统初始的易感者人数为
,记普通感染者人数达峰值时易感者人数为
,则当
时,普通感染者的人数呈现先上升后下降的趋势,当
时,普通感染者的人数呈现单调下降的趋势 [12]。
如果仅当普通感染者的人数有一定时间段的增长才认为新冠疫情在蔓延,那么
就是一个阈值,为该传染动力系统的阈值。当
时传染病就会蔓延。而提高阈值
,使得
,则传染病将不会蔓延。
在本文所建模型下,2020年2月19日的易感者人数为28,305人,因此
为28,305人。由于阈值是当普通感染者的人数达到峰值时对应的易感者人群的数量,因此,这个数值也受传染动力系统模型参数的影响。因此,传染动力系统的阈值与接触率、隔离率和治愈率等相关联。通过调整宏微观的隔离政策,可以影响COVID-19疫情的阈值,从而影响疫情规模和趋势的走向。
5.4. 隔离力度的扰动分析
模型参数
表征该传染动力系统的隔离力度,随着时间的推进,整个动力系统的隔离力度愈来愈大、防控力度不断升级。钟南山团队的研究曾指出 [13],如减低武汉管控力度,湖北可能在3月中旬出现第二次疫情高峰并延续至4月下旬。
现在,通过设定不同参数,进行隔离力度的扰动分析,直观地感受隔离力度对疫情规模的重大影响。以第三阶段2020年2月13日至2020年4月7日为例,对表征隔离力度的模型参数
设定不同初值,疫情走势见图14。

Figure 14. Perturbation analysis of quarantine level at the third stage
图14. 第三阶段隔离力度扰动分析
可见,即便隔离力度增大10倍,也不会对普通感染者人数有较大影响,而这却会对经济生产、复工复产等带来巨大代价。相反地,当隔离力度放松时,普通感染者数量急剧上升,这将导致疫情规模急剧扩大,对疫情防控带来严重危害。
因此,现有的防控力度适当有效,很好地控制住了疫情发展的规模,使得武汉地区的疫情乃至全国的疫情局势逐渐可控从而走向尾声。
6. 结语
本文针对武汉地区新冠疫情,修正传统SEIR传染病模型,建立符合新冠病毒传播特性的SEIHCD模型,对易感者、潜伏者、普通感染者、重症感染者、治愈者和病亡者的实时变化进行研究。
相较于传统模型,首先在模型上有所创新。假设潜伏者也具备传染能力,将感染者细分为普通感染者和重症感染者,移出者被具体细分为治愈者和病死者。此外,传染动力系统的模型参数非常数也是本文与传统研究显著不同之处。本文分三阶段分别对武汉疫情进行研究,重点考查人为干预对疫情发展的影响。
基于通报数据,对缺失数据进行处理,通过搜索算法得到武汉地区在该传染动力系统中有效总人数。针对数据突增,利用指数模型对普通感染者人数进行拟合,将突增数目回放到之前,得到更符合实际的每日数据。利用预处理所得数据,结合各阶段各群体初值,以最小二乘法为准则,分三阶段进行参数反演,得到各阶段下表征隔离力度和救治水平的模型参数估计值。利用所估参数,代入所建方程组,利用数值分析求解模型,得到各群体实时数量变化。结合通报数据,做出各阶段的普通感染者和治愈者的对比图。
此外,做出治愈率和死亡率的时序图,就武汉地区三个阶段的防控力度、救治水平对疫情发展规模的影响进行分析。武汉地区疫情在2月19日附近出现拐点,普通感染者的数量在该点达到峰值。该日所对应的易感者人数为一个阈值,在该传染动力系统中,若易感者的初始数目大于该阈值,则传染病会呈现扩大的趋势,即感染者的数目会先增大后减少。相反地,如果易感者的初始数量小于该阈值,该传染病则会消退,感染者的数量会呈现单调下降的趋势。
最后,对隔离力度进行扰动分析,模拟出武汉地区在隔离力度更大和更小时疫情规模的趋势走向,利用图像直观展现防控隔离的重大意义。根据计算结果和图像,三阶段武汉地区防控力度逐渐升级,隔离力度不断加大,治愈率总体呈现大幅上升。
综上所述,本文利用2020年1月10日至2020年4月7日武汉地区的疫情通报数据,修正SEIR模型从而建立SEIHCD模型,经数据预处理,分三阶段估计出模型参数并求出各群体模拟实时数量。做出图像,就模型参数、治愈率和死亡率等变化分析隔离力度对疫情规模的影响,进行阈值分析和隔离力度扰动分析,对武汉防控成果给予充分肯定。但由于新冠病毒是一种新型病毒,人类对其了解还并不全面,因此其传播特点可能并不单一和稳定。例如不同人群出现了长短不一的潜伏期,目前还出现无症状感染者的报道。对于患病后康复治愈的人是否对该传染病免疫,我们也尚不能给出定论。因此,这些都是本文研究可以进一步深化和改进的方向。
在给予武汉抗疫经验充分支持的同时,也需要指出的是,武汉抗疫过程并非无可挑剔,如更早实施武汉“封城”,疫情发展规模则会进一步被缩小。如果对武汉疫情发展阶段进行重新分段,将武汉“封城”后的估计参数代入2020年1月23日前的重新划分的阶段,可以实现对疫情规模的进一步控制。
本研究既是对武汉地区疫情的回顾,也用武汉抗疫经历为未来公共卫生和传染病防控给出经验借鉴。疫情无情,人间有爱。我国对新冠疫情的抗击似乎已经走入尾声,但是这个尾巴到底有多长暂时还无法确定。目前外防输入,内防反弹的形势仍然严峻,因此需要全国上下齐心抗疫,继续保持警惕,珍惜隔离防控打下的宝贵成果!
基金项目
国家自然科学基金项目(11671301)资助。
NOTES
*通讯作者。