1. 引言
近年来,在无人机技术及其理论不断推陈出新的同时,集群无人机作为一种新型作战模式也不再是空中楼阁 [1]。在集群无人机内部,无人机之间的相互联系十分复杂,再加上采用一些高新技术取代人来实现对飞行器的控制本身就是一件颇具风险的事情,使得集群无人机的任务可靠性成为众多学者关注的焦点。然而,尽管一些寻找故障适应性的课题正在出现,但总体来说,目前关于集群无人机任务可靠性的文献依然很少 [2]。
贝叶斯网络被广泛应用于复杂系统的可靠性研究 [3]。本文将集群无人机划分为单无人机、无人机子群、无人机集群三个层次,分析其任务可靠性,并应用贝叶斯网络对这三个层次进行建模。
2. 集群无人机
“集群无人机”是多架无人机的聚合过程,在通信网络的支持下,每架无人机共享信息,形成“无人机子群”乃至“无人机集群”,进一步发挥无人机的数量和成本优势。“无人机子群”是多架无人机的集合,无人机通过一定的规则组合起来弥补各自功能上的缺陷,使作战目的得以实现。“无人机子群”是多架无人机协同飞行,共同执行侦察、作战支援、直接打击等作战任务,相较于单无人机能够提高执行单次作战任务的任务成功率。
近年来,随着计算机技术以及无线通信技术的快速发展,使得众多无人机子群可以聚合起来形成共同完成作战任务的整体,成为“无人机集群” [4]。“无人机集群”可以认为是多个无人机子群的协同,无人机子群之间通过一定的指挥关系和协同关系来实现作战任务。
3. 集群无人机的任务可靠性分析
3.1. 单无人机的任务可靠性分析
单无人机是集群无人机遂行作战任务的最小单元,不同的无人机会有不同的任务可靠性。制约单无人机任务可靠性的主要因素有:无人机自身的系统可靠性、复杂地形环境、复杂电磁环境和异常的天气 [2]。无人机自身的系统可靠性可以通过多次的试验来得到,令其系统可靠性为Pi。另外,地形、电磁环境和天气也会影响无人机完成任务的能力。假定这三种情况对单无人机的影响参数,分别为k1、k2、k3,则单无人机的任务可靠性为:
(1)
3.2. 无人机子群的任务可靠性分析
根据无人机子群内部的控制方式,无人机子群大致可分为层级式、集中式、分布式三种。
3.2.1. 层级式子群的任务可靠性
图1表示的是由六架无人机组成的层级式结构无人机子群。整个无人机子群的任务可靠性不仅和单架无人机的任务可靠性息息相关,还受到拓扑结构的影响。在图1中,右边的三架无人机是一个串联结构,而在左边,最下层的两架无人机共同和它们的上层无人机组成串联结构,从整体结构来看,该结构是一个复杂串联结构。在计算无人机子群可靠性时,不仅要通过单架无人机的可靠性,还要结合它们的结构进行系统计算。图中的箭头表示上层无人机对下层无人机的指挥关系。
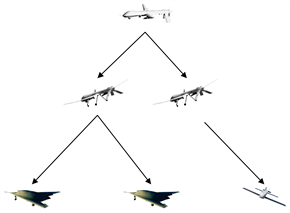
Figure 1. UAVs subgroup with hierarchical structure
图1. 层级式结构的无人机子群
层级式无人机子群的任务可靠性由直接影响任务成败的最底层的三架无人机决定,其中,左边的两架无人机只需一架正常工作即可保证无人机任务成功。层级式无人机子群的任务可靠性Pa为:
(2)
式中,Pi1表示第一层无人机的任务可靠性,Pi2表示第二层无人机的任务可靠性,Pi3表示第三层左边两架无人机的任务可靠性,Pi4表示第三层右边的一架无人机的任务可靠性。
3.2.2. 集中式子群的任务可靠性
图2表示的是集中式结构的无人机子群,一架长机指挥四架子无人机进行集群作战。所有子无人机并联和长机共同组成一个完整的无人机子群。
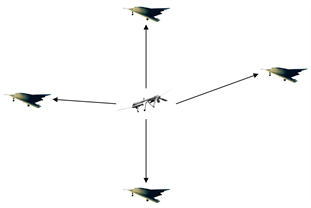
Figure 2. UAVs subgroup with centralized structure
图2. 集中式结构的无人机子群
集中式无人机子群的任务可靠性由长机及其指挥的子无人机决定,在如图所示的子群中,只需三架子无人机正常工作即可保证任务成功。集中式无人机子群的任务可靠性Pb为:
(3)
式中,Pi1表示长机的任务可靠性,Pi1表示僚机的任务可靠性。
3.2.3. 分布式子群的任务可靠性
图3表示的是由四架无人机组成的分布式结构的无人机子群,在子群中,各无人机地位相同,蜂群作战模式采用的就是这种结构,在这种作战模式下,各无人机遂行作战任务,依靠数量优势,在军事行动中占据主动权。图中的虚线表示无人机之间的双向通信。
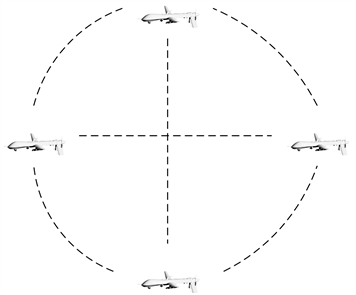
Figure 3. UAVs subgroup with distributed structure
图3. 分布式结构的无人机子群
分布式无人机子群的任务可靠性由子群中所有无人机的状态共同决定,在图3中,分布式无人机子群由四架无人机组成,三架无人机正常工作即可保证子群的任务可靠性。分布式无人机子群的任务可靠性Pc为:
(4)
3.3. 无人机集群的任务可靠性分析
在无人机集群作战中,多个无人机子群相互配合共同完成任务已经成为了一种趋势。根据作战任务的需要和实际情况,可选择一定数量的不同类型无人机子群组成无人机集群。
图4是由3个无人机子群共15架无人机组成的无人机集群结构。无人机集群采用了分布式控制方式 [5],结合了各个无人机编队的特点,具有多态性、层次性以及网络结构复杂的性质。图4由一个层级式无人机子群,一个分布式无人机子群和一个集中式无人机子群组成。图中的箭头表示指挥关系,作为多子群聚合的集群无人机,它的任务可靠性问题是集群无人机可靠性问题中最复杂的,它需要结合单无人机可靠性、无人机子群内部的结构、各子群之间的结构综合考虑。
图中,无人机集群采用了分布式控制方式指挥无人机子群,无人机子群之间相互独立、互不影响,只有图中的三个无人机子群都正常工作,才能确保无人机集群可靠。无人机集群的任务可靠性Pu为:
(5)
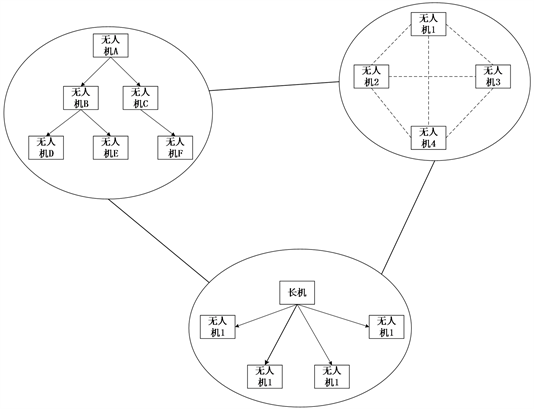
Figure 4. Network structure of UAV cluster
图4. 无人机集群的网络结构
4. 贝叶斯网络模型
4.1. 贝叶斯网络概述
贝叶斯网络借助图形理论来刻画属性之间的逻辑关系,并使用条件概率表压缩表示联合概率 [6]。详细的说,一个贝叶斯网络B由有向无环图G和参数θ两部分构成,即
。G是一个有向无环图,每一个节点对应于一个属性,根据结点之间的联系用有向线段将它们连接起来;θ用于知识表示,并基于知识使用数学公式定量表示结点之间的联系,进行不确定性推理,假设结点Xi的父结点集为Πi,则θ包含了每个结点的条件概率:
(6)
因此,利用贝叶斯网络可以将联合概率进行分解计算,并有:
(7)
4.2. 集群无人机任务可靠性的贝叶斯网络建立
集群无人机是网络结构复杂,具有层次性、多态性等特征的复杂系统,对任务可靠性的分析和建模都提出了较高的要求。集群无人机的贝叶斯网络模型如图5所示,图5中的集群无人机包括一个层级式无人机子群,一个集中式无人机子群和两个分布式无人机子群,无人机子群之间采取分布式控制方式。集群无人机的贝叶斯网络分成三个层次:单无人机,子群和集群。在图5中,HL1、HL2和HL3分别代表的单无人机、子群和集群所处的层次。HL1中的节点代表单无人机,HL2中的节点代表无人机子群,HL3中的节点代表无人机集群。HL1到HL2是单无人机聚合成为无人机子群的过程,HL2到HL3是无人机子群聚合成为无人机集群的过程。无人机集群的任务可靠性取决于各子群的任务可靠性及其通信状况,在集群无人机的三个层次的可靠性中处于最关键的地位。
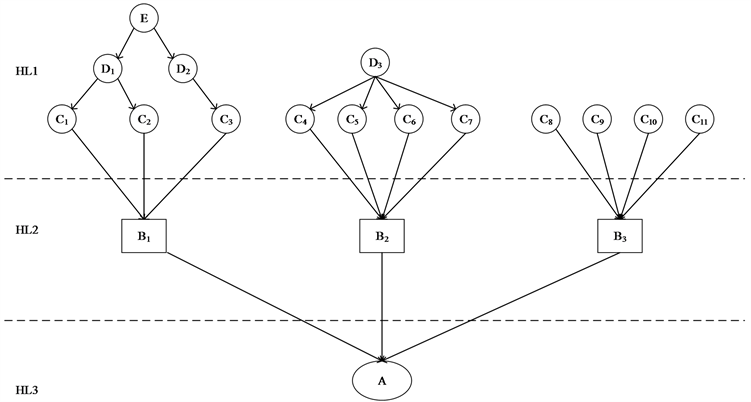
Figure 5. Bayesian network model of clustered UAVs
图5. 集群无人机的贝叶斯网络模型
4.3. 集群无人机任务可靠性的贝叶斯网络推理
如图5,B1代表集中式无人机子群,它的任务可靠性满足:
(8)
B2代表集中式无人机子群,在这种结构中,根节点D3和子元件C4,C5,C6,C7并联组成多态并联系统。从数学的角度来说,像这种一对多的关系模型,属于最基本的映射关系,因此具有非常广泛的应用,和朴素贝叶斯分类器结构十分相似,假设C4,C5,C6,C7条件独立,集中式无人机子群满足:
(9)
分布式无人机子群采用了另一种典型的结构。叶节点B3由无人机C8,C9,C10,C11串联而成,假设C8,C9,C10,C11条件独立,它的联合概率分布满足:
(10)
B1,B2,B3最后构成无人机集群A,其任务可靠性满足:
(11)
和分布式无人机子群相比较,由于控制方式是相同的,所以模型有相似的地方,不同的是节点的概率值是不一样的,这是因为无人机子群的模型中以单无人机为子模块,而集群无人机的模型以无人机子群为子模块。
5. 计算结果分析
对集群无人机进行任务可靠性计算,得到结果为0.578,通过集群无人机的拓扑结构和贝叶斯网络模型的计算结果,要提高集群无人机的任务可靠性,可从通过以下几种方法:
(1) 提高单无人机关键部件的可靠性,特别是容易受到电子干扰和恶劣天气影响的部件。单无人机是集群无人机的最小单元,提高单无人机的可靠度,特别是在集群无人机中处于关键地位的无人机,对于提高整个系统的任务可靠度具有促进作用。
(2) 增加无人机子群中并联子无人机的数量。这 样可以提高无人机子群的冗余度,从而提高整个系统的任务可靠度。
(3) 增加并联的无人机子群的数量。增加无人机子群的数量,能大幅度提高任务成功率,从而提高集群无人机的任务可靠性。
6. 结束语
随着无人机技术的发展,集群式的无人机在未来肯定会有越来越广泛的应用。同时,在未来战争中,也必然会有集群无人机的一席之地。本文从集群无人机的拓扑结构出发,结合其可能的任务环境,给出了任务可靠性的计算逻辑,并使用贝叶斯网络进行了建模,为后续的集群无人机任务可靠性研究提供了借鉴意义。