1. 引言
1957年中国火山岩油气藏在准噶尔盆地第一次被成功发现,到目前为止,该油气藏已勘探50年以上,在准噶尔盆地等11个含油气盆地中找到了火山岩油气藏存在 [1]。能够准确认识火山岩岩性是研究火山岩油藏的重要基础,但火山岩岩性复杂,矿物成分复杂多变,测井响应特征不明显,岩性识别难度极大。
前人在这方面做了很多的研究。Sanyal等人(1980)利用声波时差,中子测井曲线的交会图识别岩性 [2]。Benoit等(1980)总结了声波时差测井、中子测井等常规测井在花岗岩,玄武岩等上的响应特征 [3]。范宜仁等(1998)在新疆准噶尔盆地,根据交会图技术有效识别火山岩岩性 [4] [5]。张莹(2007)根据成像测井资料识别火山岩。谭伏霖,王志章等人(2010)鉴于取芯样本有限,采取样本扩充法识别火山岩岩性 [6] [7] [8] [9]。由于火山岩岩石类型多,仅根据单一的测井曲线很难将岩性准确识别出来,近几年许多人利用综合的信息来识别岩性,主要利用地质结合测井和数学算法方法来识别岩性。田艳等(2010)根据逐步分析法和fisher判别的方法进行岩性识别 [10]。程国建等(2010)为了提高测井在岩性识别的准确率,将粒子群优化算法(PSO)与最小二乘支持向量机相结合对实际测井资料进行岩性识别。鞠武等(2012)利用有序聚类分析方法识别岩性。李建国等(2015)利用深度神经网络结合测井资料进行岩性的识别。牟丹等(2015)基于最小二乘支持向量机识别岩性 [11] [12] [13] [14] [15]。
本文综合利用取芯,薄片,成像资料解释的岩性标签标定测井资料,形成测井和岩性标签的样本库。将样本库分为训练集(占70%)和测试集(占30%)两部分。结合机器学习中的决策树,随机森林,梯度提升树和贝叶斯方法,利用训练集建立4种火山岩岩性识别模型,利用测试集评价这4种模型的稳定性,选择最优模型。结果表明,随机森林和梯度提升树方法模型最优,可作为该研究区利用常规测井曲线识别火山岩岩性的有效方法。
2. 原理方法
2.1. 决策树
决策树是一种描述对实例进行分类的树形结构,决策树由结点和有向边组成。决策树是属性与值之间的一种映射关系。决策树算法过程包括特征的选择、树的生成和树剪枝的过程,根据特征选择的方法不一样,形成了不同的算法,主要包括ID3算法,C4.5算法和CATR算法。
ID3是决策树算法的一种,是在原始决策树算法的基础上实现的。采用的分治的思想,其主要特点是在结点上选择特征时采用的是信息增益的方法。信息熵是衡量随机变量出现的期望值,熵值越大,代表信息的不确定性越大。一般选择熵值大的特征属性作为结点的划分 [16]。计算过程是:在开始计算输入的所有属性,根据输入的所有特征属性,根据公式计算这些特征属性的信息增益,选择最大的作为分枝结点。在每个分支结点都进行此运算,最后将每个类别分到不同的叶子节点中,形成一棵决策树。当有未知样本输入时,每经过一个结点判断路径走向,最终预测类别。C4.5算法它是根据ID3算法改进,继承优势补齐缺点。其主要不同之处在于利用信息增益率来进行特征属性的选择。对这一点的改进主要是避免了进行特征属性选择时会偏向多值的特征属性的缺点。另一个优点是加入了树的剪枝功能,从而防止过拟合。此外还可以处理缺省值。CATR算法与前面两种算法不同的是,利用基尼指数值来分枝不同特征属性,并且该方法主要采用的是二分,即每个枝点都只分成两个结点,最终形成一颗二叉树。
决策树方法最重要的一个环节是确定特征属性划分方案,这个划分方案的选择主要是依据信息论的理论。假设训练数据集
,其中
为输入实例,n为特征个数,
为类标记,
为样本容量,A表示某一特征属性。设X是一个取有限个值的离散随机变量,其概率分布为
(1)
其中信息量(Intormation)和嫡(Entropy)的定义为
(2)
(3)
信息增益:
(4)
信息增益率:
(5)
基尼指数:
(6)
假设用特征A将数据集D分为D1,D2,则划分的基尼指数为:
(7)
对于决策树还有另一个种类,是回归决策树。在机器学习中每一类方法即可以用来分类,判别某一类的类别,也可以用于回归计算,计算某一个值,主要解决回归问题。在回归决策树中与分类决策树最大不同点是判断结点分支的依据不是选用信息熵的理论,而是用最小化均方差来判断选择划分特征属性。
2.2. 随机森林方法
随机森林属于组合分类器之一,由许多决策树叠加组成。分配给每棵树的样本是从数据集中随机抽取,抽完后放回,抽取数据是有放回的抽样 [17]。每抽取一次数据,就建立一颗决策树模型,重复这样的操作,最后所有的决策树就形成了一片森林,即随机森林(图1)。
该方法与决策树方法有很多相同的地方,都是属于树形结构,且每个结点的特征属性划分方法基本一致,都采用ID3,C4.5,和CATR等算法。其主要不同点是在决策树的基础上,引入了两个不同的随机条件,第一次随机是从数据集中随机的抽取训练数据集(Random subset),该抽样方法是有放回的抽样,每次抽取一次则形成一颗决策树(图1)。在决策树里,随机森林该方法采用了第二次随机条件,即对抽取的训练集中的数据的特征属性集合n中采取随机选取S(S≤n)个特征属性集合,根据这S个特征进行结点划分和决策树的生成。该方式使得生成的决策树具有随机性。正因为引入了这两个随机的特征,使得该方法相比决策树而言具有更好的效果 [18]。该方法优点主要:第一,有对训练数据不容易产生过拟合的现象。第二,在不同属性中可以判断属性的重要程度,根据选择需要可以选折几个重要的特征属性参数。第三,该方法对噪声、异常值等数据具有不敏感的性质。
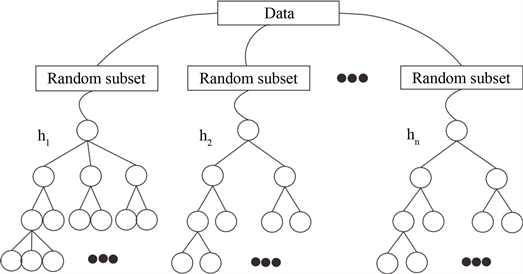
Figure 1. Schematic diagram of random forest
图1. 随机森林示意图
2.3. 梯度提升树(GBDT)方法
梯度提升树是一种迭代的回归决策树算法,由多颗决策树组成,将所有树的结论累加起来就是最终的结论 [19]。该方法是一个应用很广泛的算法,主要是用于分类和回归两方面,其次是特征的选择和创造新特征。该方法学习的过程中,因为是属于加法模型,所以无论是分类还是回归,都应用的是回归模型的决策树。在各结点分支时,不再是利用信息熵理论判断,而是选择最小化均方差来判断结点分支。均方差最小的作为分支判断依据。
该方法主要有两个不同特点。第一种是提升树,即残差方式生成的树。在所给的数据中学习时,最开始是先生成一颗回归决策树。然后根据这颗树的结果与真实值做差值,得到了残差,然后根据每个数据的残差的值再生成一颗决策树。到第m步的决策树模型表达式为
(公式8)。其中参数
主要依据公式(1.9),计算残差得到。以此类推,最后得到一个误差较小的树,利用前向分布算法最终把所有的树结合起来即是该方法的分类或回归的决策函数模型(公式10)。
(8)
是第m次的决策树;
为前
步生成的模型;
是当前生成的模型,
为决策树参数。
(9)
(10)
第二种是梯度提升树,也是本文所应用的树。该方法也是每一颗树学习前N-1棵树的残差,直到最后得到分类或回归误差最小的树。与第一种不同的是,该方法利用的是梯度下降的方向求解误差值,这样求解的是局部最优解。而做残差求解是求的全局最优,但仍然选择梯度下降的方向求解,主要是因为该方法灵活,可以方便求解分类和回归问题,并且只要能求导的损失函数都可以使用,可以防止过拟合。对于平方差损失,其二者方法求解方法相同。
梯度提升树的算法过程为:
输入训练集
,损失函数
,迭代的次数为M。
1) 使用常量值初始化模型
其中
是常数。
2) 迭代训练模型
For m = 1:M
计算伪残差:
(11)
其中
将残差rim 拟合到回归树hm(x) 中,即hm(x) 的训练集为{(xi, rim)}
计算乘数
(12)
更新模型
(13)
优点:1) 能够允许不同特征组合拥有不同的判别式;2) 对非线性数据有着很好的处理效果;3) 能解决数据缺失问题;4) 可以自动进行特征选择 [20]。
2.4. 朴素贝叶斯方法
在机器学习中主要有两种模型,一种是判别模型,另一种是生成模型。前三种是判别模型,贝叶斯是属于生成模型,从数据中学习到联合概率分布,再求出条件概率分布。朴素贝叶斯法分类主要是根据已知的数据学习计算出先验概率,在根据条件独立性假设计算条件概率,最后计算后验概率,对未知数据集进行预测。
设输入的χ属于Rn为n维向量的集合,输出的类标记集合为
,输入的向量x属于χ,输出的不同类y属于l,X为空间χ上的随机向量,Y为空间l上的类别标签。训练数据集为:
在训练数据集中计算先验概率和条件概率。最后得到后验概率。
先验概率分布:
(14)
条件概率分布:
(15)
条件独立性假设:
(16)
根据已经计算的先验概率和条件概率,即可根据贝叶斯理论公式构造出预测模型。对于未知数据x,加载到前面模型,计算出后验概率
,选择后验概率最大的为x的输出类。后验概率计算公式为:
(17)
则朴素贝叶斯法分类的基本公式:
(18)
上式中分母对所有ck都是相同的,所以得到分类器为,
(19)
贝叶斯算法的缺点是建立在样本属性独立性假设的基础上,所以如果样本属性有关联时其效果不是很好 [21]。
3. 研究思路及流程
以关键井,作为重要标签井,利用常规测井和非常规测井资料、取芯资料、通过交会图来判断不同测井开展岩性特征分析,选取对岩性敏感的常规测井系列,如选取“GR”、“SP”、“CAL”、“AC”、“RT”等,以取心井岩心描述组为标签数据。
建立岩性知识库组成训练集,利用机器学习的决策树、随机森林、梯度提升树、贝叶斯等算法,根据优选的测井参数和机器学习建立岩性分类模型,对所建立的各种算法模型进行评价,优选出较好的算法模型,再对未知井段的岩性利用该模型进行预测。见图2、图3流程如:

Figure 2. Flow chart of machine learning
图2. 机器学习流程图

Figure 3. Flow chart of intelligent identification and prediction of complex volcanic rocks
图3. 复杂火山岩岩性智能识别及预测流程图
4. 应用实例
金龙2井区块位于准噶尔盆地西北缘中拐凸起东斜坡带。目的层位于二叠系佳木河组的火山岩地层,岩性复杂,储集空间类型多。根据研究区8口取芯井数据,薄片数据,实验分析化验数据可知,研究区火山岩岩性主要分为熔岩类和火山碎屑岩类,熔岩类包括玄武岩,安山岩,英安岩和流纹岩4种。火山碎屑岩类包括熔结角砾岩,火山角砾岩和凝灰岩3种。
4.1. 火山岩岩性常规测井响应特征
测井的响应主要是应为地下岩石的组分、流体类型、裂缝等综合的影响。其主要的影响程度最高的是岩石的类型。不同的岩石类型其岩石的化学成分、矿物成分等有很大不同,导致测井有不同的变化特征。对于电阻率测井,火山岩岩石越致密电阻率越高,熔岩类的电阻率高于火山碎屑岩类 [22] [23] [24]。熔岩中英安岩裂缝发育较少,致密,电阻率很高,安山岩,流纹岩和玄武岩等由于裂缝和气孔的因素影响导致电阻率会偏低。
自然伽马测井的响应特征与岩石的放射性有关,而岩石的放射性与岩石的矿物成分有关。在火山岩中,岩石的放射性与岩石属于基性岩,酸性岩等有关。从基性到酸性逐渐增加 [25] [26]。在该研究区目的层内,玄武岩自然伽马小于26 API,安山岩在45 API左右,英安岩和流纹岩高伽马,大于65 API,在相同类岩石中,放射性的大小还与岩石的结构有关。从熔岩到火山碎屑岩,放射性增加。凝灰岩自然伽马在60 API左右,熔结角砾岩低伽马,25 API左右,火山角砾岩中伽马,50 API左右。
中子测井主要反映的是地层的孔隙情况。该地区目的层中,凝灰岩本身相对火山岩而言,不是很致密,存在孔隙,测的中子值也比较大,在25%左右。火山角砾岩和熔结角砾岩也存在较大的原生孔隙,测的中子值约20%左右,是该区主要储层。安山岩由于裂缝比较发育中子值约17%左右。玄武岩由于发育杏仁构造,中子测井值较高,约25%。流纹岩和英安岩发育致密,中子测井值较低,约10%左右 [27]。
密度测井一般而言,由基性到酸性的火山岩,该测井值会逐渐变小 [28]。流纹岩为酸性的喷出岩,密度较低。安山岩为中性的喷出岩,密度相对流纹岩较高,为2.54 g/cm3左右。玄武岩为基性的喷出岩,密度最高为2.7 g/cm3左右。在同类岩石中,火山碎屑岩的密度则低于熔岩。
声波时差测井在火山岩石中,火山碎屑岩的致密程度低于熔岩类,其声波时差会高于熔岩 [29] [30]。火山角砾岩和熔结角砾岩声波时差在65 μs/ft左右。凝灰岩的致密程度最低,声波时差最高,约80 μs/ft。英安岩最致密,声波时差最低约57 μs/ft左右。玄武岩,流纹岩和安山岩声波时差约60 μs/ft。
成像测井反映周围岩石电阻率的变化,由一种渐变的色板(黑–棕–黄–白)对电阻率由低到高进行刻度,常用来识别结构和构造。一般分为静态平衡图像和动态加强图。静态图采用统一配色,展现井段电阻率的改变。动态图是采用分段配色,突出局部相对微电阻率的变化(颜色由深到浅,电阻率由小到大)。所以利用静态图可以区分沉积岩和火成岩 [31] [32]。利用FMI动态图可以识别火山碎屑岩(角砾岩和凝灰岩)和具有流纹构造的流纹岩。利用动态图和常规测井曲线可以识别英安岩,安山岩和不具流纹构造的流纹岩。该方法特点是能通过辨别岩石结构和构造来区分岩性。英安岩FMI图像呈块状构造,火山角砾岩呈角砾结构,流纹岩呈流纹构造。凝灰岩呈凝灰结构。见图4。

Figure 4. Log response characteristics of volcanic rock
图4. 火山岩测井响应特征
4.2. 交会图分析
前人在识别火山岩的识别中,主要利用交会分析法,在交会图上描述不同岩性的特征。该方法优点是简单直观。缺点是利用特征太过单一,不具有代表性,错误率较高。本文采用机器学习的方法的优点是可以融合前人所有研究的方法特点。本文采用交会图分析不同岩性特征,提取敏感特征 [33] [34] [35] [36]。
特征选取的个数对岩性预测的结果影响非常大。假如只有一个特征,即在一维空间中,如图5,在对角上面的GR,DT,CNL,RHOB,RT,RI,即岩性在一维空间中的响应分布,很难把各类岩性区分开。在二维空间上,即选择两个特征的交会图分析,相比一维特征,岩性的分类效果较好。
4.3. M-N交会图
岩性识别前人除了利用常规的测井曲线交会图,还有其中确定岩性模型M-N交会图,主要应用中子、密度和声波三种孔隙度测井。该交会图主要目的是消除孔隙度的影响因素,而突出岩性的作用(如图6)。M,N定义为:
(20)
(21)
式中:
为声波时差的流体值和测井值;
为密度的流体值和测井值;
为中子的流体值和测井值。
在火山岩中最主要的是裂缝对M、N的影响。当地层中的储集空间主要是裂缝时对M、N的值有影响。当储层中发育裂缝时,且裂缝为高角度或垂直裂缝时,声波时差不受裂缝的影响,而密度测井值降低,因此导致M值将增大,而对于N值结果趋于保持不变。所以,当地层中发育高角度裂缝时,数据点向M值增大的方向移动,N值基本不变。当地层发育低角度缝时,声波时差测井值明显增大,此时M、N值不受裂缝的影响。假如裂缝很发育,声波时差出现“周波跳跃”现象时,M值会变小。
4.4. 机器学习岩性识别
利用机器学习建立岩性分类及预测模型,具体包括:样本库的建立;特征选择;测井特征数据的归一化;训练模型;评价模型以及岩性预测。
1) 样本库建立
根据取芯资料、测井数据和成像测井数据,分析测井数据与岩性的对应关系,生成样本空间。
2) 特征选择
前面已经具体分析了测井响应特征,优选岩性敏感的测井曲线,即GR,DT,RHOB,CNL,RT,RI。同时构造两个新的特征,即M和N。最终确定的岩性敏感特征为:GR,N,RI,M,CNL,DT,RT,RHOB 8种特征,其占用的权重比依次为0.22, 0.18, 0.16, 0.13, 0.11, 0.08, 0.07, 0.05。
3) 测井数据归一化
测井数据的预处理对推广到多井的岩性识别具有相当重要作用,因为相同的岩性数据利用不同规格仪器测量时,数值上会存在一定的系统偏差。数据归一化处理可以消除量纲影响,降低不同测井仪器测量绝对值误差导致的影响,利于后期建立的模型对全区井段都能有很好的预测效果。因此将前面选取的8种特征全部归一化到[0, 1]中。对于GR,DT,RHOB,CNL,M,N采用线性变量的归一化,即:
(22)
对于电阻RT,RI采用先取对数,在归一化,即:
(23)
如何选取变量的最大值和最小值变的格外重要,如果直接采用该变量的最大值,那么一些极端值会参与运算,干扰主体数据的归一化。为准确获得最大值和最小值,采用累积概率曲线一次导(斜率)的方法来获取特征的最大和最小。
根据各特征的数据,绘制累积概率分布曲线,曲线形态一般是从小到大数据的累积百分比变化很小,到达一定临界值时,数据变化开始变大,将这个临界值作为特征曲线的最小值,到达最后,数据变化慢慢变小,到达一个临界值后数据变化趋于稳定,把这个临界值作为该特征曲线的最大值,如下图7所示,在对JIN202井DT进行归一化时,根据两个的临界值取得最大值为121 us/ft,最小值为57 us/ft。原始DT数据分布范围为[48, 157],剔除极端值后数据分布范围为[57, 121],极端值占据数据范围比例为41.3%,极端值占数据量比例为3%。
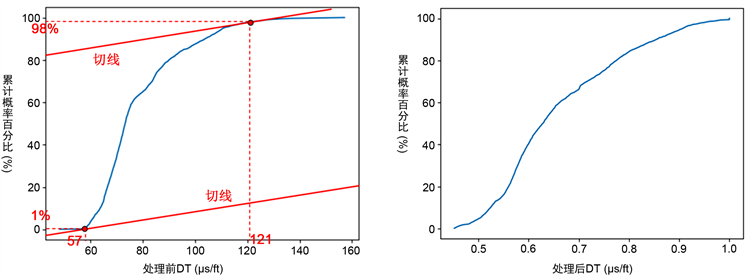
Figure 7. The cumulative probability curve of JIN202 DT before and after normalization
图7. JIN202 DT归一化前后累积概率曲线
4) 参数优选
根据前面建立的标签样本数据库,各类岩性标签总数为4745个,将样本数据随机切分为训练集和测试集,训练集占70%,数量为3321个岩性样本点,测试集占30%,1154个岩性样本点。训练集用来训练模型,测试集用来检验模型的适用性,最终用该模型推广到全区。利用机器学习算法从数据集中学习到良好并稳定的模型,对于参数的选取至关重要。在参数选择的过程中,为了防止过拟合现象,本文采用交叉验证的方式,将数据集采用5折交叉验证。参数类型中,criterion指定决策树结点切分质量评价准则。min_samples_split参数指定每个内部节点(非叶节点)包含的最少样本数。min_samples_leaf指定每个叶节点包含的最小的样本数。learning_rate为每个学习器的学习率,就是权重的缩减系数或步长,取值范围为[0, 1]。n_estimators:即弱学习器的最大迭代次数,或者是最大的弱学习器的个数。一般来说n_estimators太小,容易欠拟合,n_estimators太大,容易过拟合,一般选择一个较好的适中值,调参过程中与learning_rate一起考虑。subsample抽取子样本的比例,取值为(0,1),如果小于1,则有部分样本去做GBDT的决策树拟合,小于1的比例可以减少方差,防止过拟合,但会增加拟合偏度,一般选择在[0.5, 0.8]。图8、图9、图10、图11展现了决策树,随机森林和梯度提升树的各个参数优化。表1列出了不同方法最后的搜索结果。
 (a) criterion和depth参数
(a) criterion和depth参数 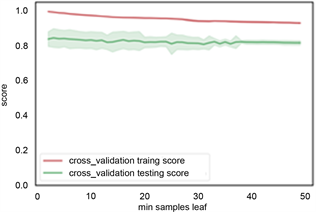 (b) min samples leaf参数
(b) min samples leaf参数 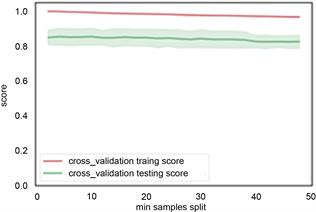 (c) min samples split参数
(c) min samples split参数
Figure 8. Decision tree parameter optimization
图8. 决策树参数优选
 (a) criterion和depth参数
(a) criterion和depth参数  (b) estimator 参数
(b) estimator 参数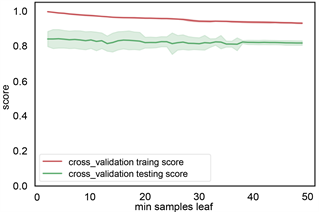 (c) min samples leaf参数
(c) min samples leaf参数  (d) min samples split参数
(d) min samples split参数
Figure 9. Random forest parameter optimization
图9. 随机森林参数优选

Table 1. Parameter selection values of different methods
表1. 不同方法的参数选择值
5) 模型评价
a) 表2和表3是各类方法在训练和测试集上的查准率,是所有预测为该岩性的结果中真正是该岩性的比例。如在训练集上,随机森林方法在安山岩上查准率最高,表明预测为安山岩的结果中,真正是安山岩的概率最高0.956,并且在测试集上随机森林准确率最高。

Table 2. Precision and recall rate of the test set
表2. 测试集的查准率和召回率


Table 3. Precision and recall rate of training set
表3. 训练集的查准率和召回率
b) ROC曲线。
TPR代表将正类样本分对的概率,FPR代表将负类样本错分为正类的概率。ROC空间中,每个点的横坐标是FPR,纵坐标是TPR。ROC曲线中,(0,0)代表所有样本全部被判定为负类,(1,1)代表所有样本被判定为正类,(0,1)代表最完美分类。通过二维ROC曲线图形,能很直观的比较不同分类器模型的分类性能。从图11中看出,随机森林和梯度提升树的性能较好,能很好的向(0,1)点靠近。其次是决策树,而贝叶斯方法较差。
c) AUC值。图11中“0”代表安山岩,“1”代表火山角砾岩,“2”代表流纹岩,“3”代表凝灰岩,“4”代表熔结角砾岩,“5”代表玄武岩,“6”代表英安岩。根据AUC值都接近1可知,随机森林和梯度提升树方法效果较好,每种岩性的AUC值都很接近于1。
 (a) 梯度提升树ROC曲线
(a) 梯度提升树ROC曲线 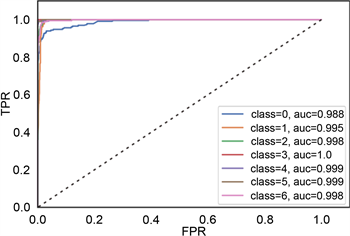 (b) 随机森林ROC曲线
(b) 随机森林ROC曲线  (c) 决策树ROC曲线
(c) 决策树ROC曲线 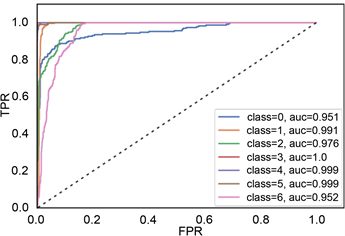 (d) 贝叶斯ROC曲线
(d) 贝叶斯ROC曲线
Figure 11. ROC curves of different models
图11. 不同模型ROC曲线
d) 模型稳定性
利用机器学习中的学习曲线判定训练模型的好坏。学习曲线中,横坐标为岩性样本数据量,纵坐标为准确率。主要评估样本数据量的大小的变化对模型的影响。本次岩性识别岩性数据样本为4745个数据,每次从这些数据中按照不同比例随机抽取样本数据,本论文主要是在[10%, 100%]之间切分出500个不同比例的样本数据集,并分训练集和测试集。为确保模型的准确,采用交叉验证的方式在抽取的样本数据集内训练和测试,本次采用5折交叉验证。在梯度提升树和随机森林学习方法中,开始抽500~1000的岩性样本数据中,训练集上准确率高,测试集上准确率低,属于低偏差,高方差,模型处于欠拟合状态,随着数据点的增加,训练集上准确率下降缓慢,测试集上准确率明显升高,且方差变小,当数据点达到4745时,模型达到了低偏差低方差的稳定状态。在决策树模型中,根据学习曲线,上下波动,模型不稳定。在贝叶斯模型中,训练集准确率较低,且在随数据增大过程中,方差发生由大变小再变大的过程,模型不稳定。所以综上所述,梯度提升树和随机森林模型较稳定,见图12。
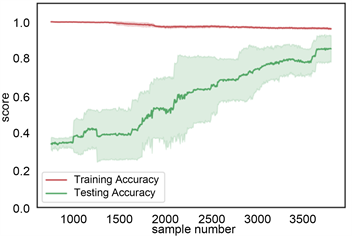 (a) 梯度提升树学习曲线
(a) 梯度提升树学习曲线 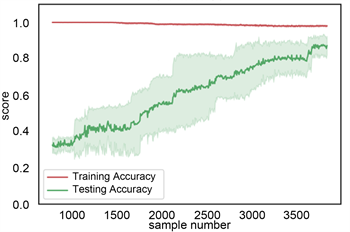 (b) 随机森林学习曲线
(b) 随机森林学习曲线  (c) 决策树学习曲线
(c) 决策树学习曲线  (d) 贝叶斯学习曲线
(d) 贝叶斯学习曲线
Figure 12. The learning curve of different models
图12. 不同模型学习曲线
5. 预测效果
根据前面建立的模型对未知井段进行预测,为验证预测的准确性,采用前面未参与建模的取芯井进行预测验证。本文选取JIN204井和KE301井。JIN204有三段取芯,第一段深度为4193.3~4198.1 m,厚度为4.8 m,取芯描述为安山岩。根据统计在该段随机森林方法预测为安山岩厚度为4 m,预测准确率为83%。决策树方法预测厚度为3.45 m,预测准确率为72%。贝叶斯方法预测厚度为4 m,预测准确率为83%。梯度提升树(GBDT)方法预测安山岩厚度为2.88 m,预测准确率为60%。第二段取芯深度为4289.4~4294.2 m,厚度为4.8 m,从图上可知,随机森林、决策树、贝叶斯和梯度提升树(GBDT)都预测准确为流纹岩,准确率为100%。第三段取芯深度在4329.3~4329.9 m,取芯描述该段岩性为流纹岩和凝灰岩,在深度为4329.9~4330.5 m的凝灰岩,随机森林和梯度提升树准确预测,而贝叶斯和决策树则预测错误。由于该段的测井曲线变化较大,流纹岩部分均未预测出来。在KE301井中(见图13),在图片道中,从上往下,深度为3852.83 m、3854.28 m和3855.03 m处的薄片定名均为安山岩,与四种方法预测均吻合。在3849.0~3852.75 m的深度段内,自然伽马,电阻率测井数据均有较明显的变化,在该段随机森林方法较好预测出来,见图14。

Figure 13. Lithology prediction of Well KE301
图13. KE301井岩性预测

Figure 14. Lithology prediction of Well JIN204
图14. JIN204井岩性预测

Figure 15. The results of intelligent recognition of lithology in multi-well volcanic reservoirs
图15. 多井火山岩油藏岩性智能识别成果图
通过对四种方法的模型评价与优选表明,较好的模型有随机森林和梯度提升树两个模型。随机森林方法的准确率为0.96,梯度提升树方法准率为0.94,相差不大,根据盲井预测的统计结。如图15所示,利用常规方法进行复杂火山岩油藏岩性识别,符合率为70%左右,而通过机器学习,特别是随机森林方法识别,符合率提高到93%以上,效果显著。
6. 结论
1) 结合取芯,薄片,成像,实验分析化验数据确定岩性,并跟据测井响应特征分析标定测井曲线对应的岩性,形成测井曲线和岩性对应样本库,为后面机器学习训练预测打下基础。
2) 根据建立的样本库数据,对数据进行归一化处理,利用机器学习中的决策树,随机森林,梯度提升树和贝叶斯方法,采用交叉验证和网格搜索优选每个模型的最优参数,建立四种机器学习模型,并对这四种不同模型评价优选,优选出最优的随机森林方法模型。
3) 利用前面优选出学习最优的随机森林模型,对该研究区45口井岩性智能解释,通过对取芯井段的统计验证,与井段取芯的符合率在90%以上。
NOTES
*第一作者。
#通讯作者。