微波加热金属导体的仿真研究

Simulation Study on Microwave Heating of Metallic Conductor

摘要: 基于有限元软件COMSOL Multiphysics，建立了置于谐振腔的铜电极的电磁场与热传导双向耦合模型。在解析铜电极热源的基础上，通过加热位置的参数化扫描，确定了铜电极在腔体中加热效率最高的最佳位置。其次，研究了铜表面粗糙度与温度之间的关系，发现表面粗糙度在0~10 μm时温度急剧递增，在10~50 μm时温度平缓，稳定在2250℃~2264℃之间。该温度已达到激发液下等离子体条件。

Abstract: Based on finite element software COMSOL Multiphysics, a bidirectional model of electromagnetic field and thermal conductivity of copper electrode that placed in the resonant cavity is established. The optimal position that has the highest thermal efficiency is confirmed by parametric sweep of coordinates based on analyzing its heat source. In addition, the relation between electrode’s surface roughness and its temperature is researched. It is found that the temperature increases drastically with the surface roughness of 0~10 μm. It becomes relatively stable at 2250˚C~2264˚C of 10~50 μm, which is able to stimulate to generate in-liquid plasma.

1. 引言

微波是一类频率介于300 MHz和300 GHz的电磁波，微波加热方法具有非接触式加热、选择性加热、快速加热及体积加热等特点 [1]。不同材料与微波产生作用机制不同 [2]：对于低复介电常数的塑料而言，其吸波能力较差，微波能利用率低；对于具有良好绝缘性和耐热性的玻璃，其不与微波产生作用，吸波能力差，而容易穿透；而对于金属而言，可以根据其三种存在形态(块状、粉末状、尖端金属)分为反射、烧结、放电 [3]。对于块状光滑金属而言，微波与其发生作用仅局限于金属表面，无法进行体加热，表现为反射电磁波。同时金属作为良导体，在电磁场下存在明显趋肤效应，交变电磁场在金属表面感生出表面电场，产生的感应电流只分布在其表层，引起焦耳热 [2]。微波频率愈高，金属导电能力愈强，趋肤效应愈明显，趋肤深度 $\delta$ 亦愈小。

Satoshi Horikoshi，Nick Serpone等人 [4] 提出一套利用微波加热金属电极(Electrode)产生等离子体的反应装置，如图1所示。在该装置中微波发生器(MW generator)产生微波，波导管(Waveguide)将微波导入腔体，微波在腔体中连续发射，最终部分微波在电极表面产生感应电流引发焦耳热，电极顶端产生2000℃以上的高温从而激发等离子体产生。

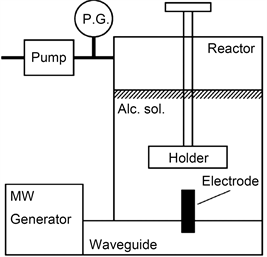
Figure 1. Apparatus of microwave heating of metallic electrode to generate plasma [4]

图1. 微波加热金属电极产生等离子体的反应装置 [4]

Ismail Rahim等人 [5] 曾利用类似的装置在2.45 GHz微波和磁控管功率为700 W的条件下激发金属表面产生高温，激发可燃冰产生等离子体获取氢能。

利用微波加热金属电极产生等离子体在纳米材料制备、水处理、可燃冰开采以及金刚石薄膜制备等方面已经获得了广泛应用，可是如何利用电磁波在金属导体表面传播来获得高温却鲜有报道。本文利用有限元仿真软件COMSOL Multiphysics，建立了一套电磁–固体传热双向耦合模型，研究了金属电极在腔体中的位置和表面粗糙度对金属电极温度的影响，结果表明金属电极的位置是获得高温的关键。

2. 加热装置和模型参数

加热装置如图2所示，包含波导、谐振腔、铜电极及波源四部分构成。谐振腔宽度270 mm，深度为235 mm，高度180 mm；波导宽度40 mm，深度114 mm，高度74 mm。其中，对腔体棱边进行倒圆角处理，半径为15 mm。电极的几何形状是圆柱体，半径为1.5 mm，长度为200.5 mm，考虑铜表面存在粗糙度，并且设为10 μm。铜的初始温度为20℃，微波频率2.45 GHz，端口馈入微波功率500 W，矩形波导的TE10为主模。谐振腔内部充满空气，仿真加热时间固定在1.5 min，时间步长0.05 min。

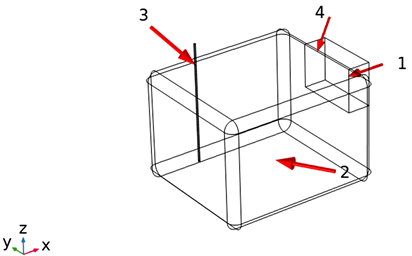1.MW (f = 2.45 GHz)；2.谐振腔；3.铜电极；4.波导(P = 500 W)

Figure 2. Schematic diagram of microwave heating apparatus in simulation

图2. 微波加热装置示意图

考虑到铜电极与波导馈入的电磁波最大限度地发生作用，同时防止铜局部温度过高而烧蚀腔体内壁，因此在进行数值仿真之前，将铜电极固定于距z = 0的平面15 mm的xy平面，并且至少与各腔体边界相距15 mm，即允许其x坐标变化范围在15~255 mm，y坐标变化范围在15~220 mm。通过参数化扫描分别沿x轴和y轴每间隔5 mm进行一个坐标点计算，统计xy平面内各坐标点铜电极的温度以及其他变量，最终绘制成数值分布云图。

3. 条件假设与边界条件

为了简化仿真模型，作出以下假设：

假设1，铜电极在微波加热过程中无热膨胀也不发生相变。

假设2，铜电极无热辐射，和周围空气也无热对流，故施加热绝缘边界条件。

假设3，金属波导及谐振腔边界被视为完美电导体，仅全反射电磁波。

根据假设1、2、3，相应边界条件分别为：

1) ${\epsilon }_{th}=\alpha \left(T-T_{ref}\right)$ (2.1)

其中 ${\epsilon }_{th}$ 为热应变， $T_{ref}$ 为参考温度20℃， $\alpha$ 为热膨胀系数(1/K)，且令 $\alpha$ 为0。

2) $-n\cdot q=0$ (2.2)

即边界传导热通量为0。

3) $n\times E=0$ (2.3)

式中n为金属壁的外法向单位矢量，E是导体外部的电场。

当铜电极处于腔体加热时，德拜媒质的电磁场计算可由式(2.4) Helmholtz方程 [6] 给出：

$\nabla \times {\mu }_r^{-1}\left(\nabla \times E\right)-k_0^2\left({\epsilon }_r\left(T\right){\epsilon }_0-\frac{j\sigma \left(T\right)}{\omega }\right)E=0$ (2.4)

$k_0=\omega \sqrt{{\mu }_0{\epsilon }_0}$ (2.5)

式中 ${\mu }_r$ 表示相对磁导率，E为电场强度(V/m)， $\sigma$ 和 $\omega$ 分别为电导率及角频率。 $k_0$ 为自由空间波数， ${\mu }_0$ 和 ${\epsilon }_0$ 各自代表真空磁导率和真空介电常数。

铜的复相对介电常数 ${\epsilon }_r$ 和自身的温度相关，且满足Debye模型理论 [7]：

${\epsilon }_r\left(T\right)={\epsilon }_{\infty }+\frac{{\epsilon }_s-{\epsilon }_{\infty }}{1+j2\pi f\tau }$ (2.6)

$\tau$ 为弛豫时间。其中， ${\epsilon }_{\infty }=5.5$， ${\epsilon }_s=9\times {10}^{-4}{T}^2-0.403T+88.1$， $\tau =9.47\times {10}^{-10}/{\left(T+22.05\right)}^{1.23}\text{s}$

对铜电极表面施加过渡边界条件 [8]：

$J_{si}=\frac{E_{ti}}{Z_s},i=\text{up},\text{down}$ (2.7)

$Z_s=\sqrt{\frac{{\mu }_0{\mu }_r}{{\epsilon }_0{\epsilon }_r\left(T\right)-j\sigma \left(T\right)/\omega }}$ (2.8)

式中 $J_s$ 和 $Z_s$ 分别表示表面电流密度和表面阻抗， $E_{ti}$ 为铜上下侧切向电场。

同时考虑铜表面阻抗受表面粗糙度及趋肤深度影响，所以其边界方程 [9]：

$Z_{rough}=Z_{smooth}\cdot \left[1+\frac{2}{\pi }{\tan }^{-1}\left(1.4{\left(\frac{{\text{Δ}}_{RMS}}{\delta }\right)}^2\right)\right]$ (2.9)

其中趋肤深度 $\delta =\sqrt{\frac{2}{\omega \mu \sigma \left(T\right)}}$， $\mu$ 为绝对磁导率。

基于电磁场和传热场的双向耦合，微波的电磁能转化为铜的热能，相应的耦合方程：

$\rho C_p\frac{\partial T}{\partial t}=\nabla \cdot \left(k\nabla T\right)+Q$ (2.10)

式中 $\rho$ 、C_p、k分别表示铜的密度、恒压热容、热导率，且均与温度相关。Q为本模型的电磁热源。

4. 铜电极热源及其温度场

热源可依据不同的分布几何特征有以下四种类型：体热源、边界热源、线热源、点热源。由于本模型中铜电极施加的物理场条件不涉及线条件和点条件，因此体热源和边界热源均为铜电极的热源。

以电磁功率损耗密度Q_e (W/m³)表示的体热源由电阻损耗Q_rh和磁损耗Q_ml两项贡献所得 [8]：

$Q_e=Q_{rh}+Q_{ml}$ (3.1)

$Q_{rh}=\frac{1}{2}Re\left(J\cdot E^{*}\right)$ (3.2)

$Q_{ml}=\frac{1}{2}Re\left(i\omega B\cdot H^{*}\right)$ (3.3)

式中B为磁通量密度， $E^{*}$ 和 $H^{*}$ 分别表示电场强度和磁场强度的共轭复数。

作为边界热源，表面损耗Q_sh (W/m²)被Q_e映射到模型传热部分的边界上 [8]。和Q_e类似，由表面电阻损耗Q_srh和表面磁损耗Q_sml两项贡献所得：

$Q_{sh}=Q_{srh}+Q_{sml}$ (3.4)

$Q_{srh}=\frac{\omega {\epsilon }_0{{\epsilon }^{″}}_r{\displaystyle \sum {\left|E_{t,i}\right|}^2}}{4k^{″}}$ (3.5)

$Q_{sml}=\frac{\omega {\mu }_0{{\mu }^{″}}_r{\displaystyle \sum {\left|\frac{E_{t,i}}{Z_c}\right|}^2}}{4k^{\text{'}\text{'}}}$ (3.6)

式中 $k^{″}$ 、 $Z_c$ 、 $E_{t,i}$ 分别表示波数虚部、特性阻抗(Ω)、含方向分量的切向电场， $i=x,y,z$。

${{\epsilon }^{″}}_r$ 和 ${{\mu }^{″}}_r$ 分别代表材料边界的相对介电常数虚部及相对磁导率虚部。 ${{\epsilon }^{″}}_r$ 为外加磁场作用下，介质电偶矩重排引起损耗的量度， ${{\mu }^{″}}_r$ 为外加磁场作用下，介质磁偶矩重排引起损耗的量度，二者承担着电磁波吸波能力，它们引起能量的损耗 [2]。铜属于非铁磁性材料， ${{\mu }^{″}}_r$ 为0，则 $Q_{sml}$ 亦为0，故 $Q_{sh}=Q_{srh}$。由式(3.5)可见电场强度对Q_sh的影响更大。

分别对Q_e和Q_sh积分，即可获得铜电极整体的电磁损耗。图3给出二者在xy平面上的数值分布。

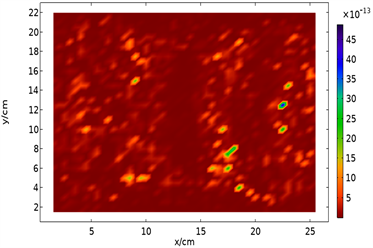(a) Q_e 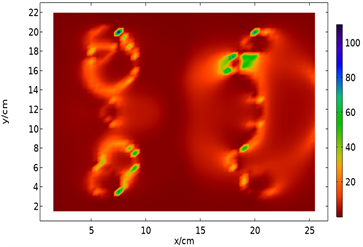(b) Q_sh

Figure 3. Numerical distribution of heat source in xy plane

图3. Q在xy平面的数值分布

对比它们的分布云图，发现其分布规律并不相同，而且Q_e极小，数值集中在5 × 10⁻¹³~4.5 × 10⁻¹² W，趋近于0，可忽略其对铜的加热效果。因此推断Q_e并非热源。为进一步验证Q_sh是唯一热源，在xy平面内选取某一点(7.5, 20)作为计算点，并维持相同的加热时间，通过以下手段：将全耦合模式(Q_e + Q_sh)更改为手动耦合，分别计算出以Q_e和Q_sh作为独立热源时铜电极的温度场。对多切面形式的温度场剖面图进行比较，结果如图4所示。

(a) Q_e + Q_sh的温度场 (b) Q_e的温度场 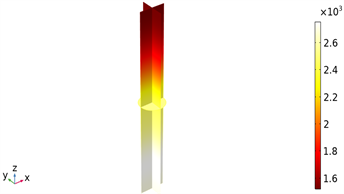(c) Q_sh的温度场

Figure 4. Temperature distribution of copper electrode using Q_e + Q_sh, Q_e, Q_sh as heat source respectively

图4. 分别以Q_e + Q_sh、Q_e、Q_sh作为热源时铜电极的温度分布

显而易见，当Q_e作为热源时，铜电极的温度没有变化，仍为初始温度20℃。此外，图4(a)和图4(c)的温度分布是完全一致的。综上所述，Q_sh为真正热源。这也说明由于趋肤效应的存在，微波无法对铜电极进行体加热，它与金属铜之间的相互作用仅局限材料表面，所以感应电流引起的焦耳热使铜电极表面先被加热，然后热量以热传导的方式沿铜表面的法向和切向传递，经过一定的时间整体受热作用明显。

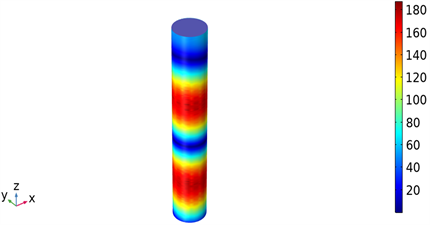
Figure 5. Distribution of $\left|E_{t,i}\right|$

图5. $\left|E_{t,i}\right|$ 分布

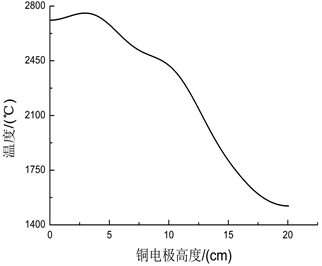
Figure 6. Temperature change of copper electrode along z direction

图6. 铜电极沿z方向的温度变化

通过图4(c)铜电极的温度场，发现其整体温度并非一致，存在温度最高点(2754.8℃)和最低点(1521℃)，并且伴随电极高度增加而连续变化，即沿z轴方向存在温度梯度，呈现递减的趋势。铜电极截面是一个等温面，且大小与外围“截线”温度数值相等。由于微波在金属壁和铜表面间不断反射，且反射后在腔体内形成谐振，进而造成谐振腔电磁场分布不同，总存在电磁场较强以及电磁场较弱的区域。特别地，当铜电极的一部分处于电磁场较强区域而另一部分处于电磁场较弱区域时，就会造成加热的不均匀，而且不随时间改变 [10]。图5给出了铜电极表面切向电场分布。此外，铜电极的一端并未处于交变电磁场的作用下，意味着Q_sh仅存在于电极的部分表面，这亦会影响其受热均匀性。由式(3.5)和(2.10)可得，铜电极整体温度存在一定的差异，其温度场存在温度梯度，如图5，图6所示。因此下文引用平均温度来度量铜电极整体的温度变化。

5. 加热位置对平均温度和|S₁₁|的影响

5.1. 平均温度

加热位置对铜电极平均温度起决定性作用，且位置对温度的影响是跳跃的，不连续的，这由图7可以看出。

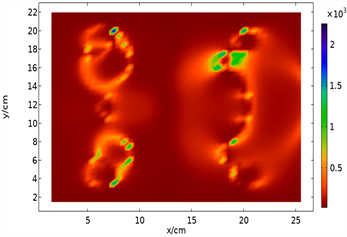
Figure 7. Numerical distribution of mean temperature in xy plane

图7. 平均温度在xy平面的数值分布

每个位置点的平均温度差异较大，最低仅比室温高0.469℃ (20.469℃)，最高可达2253℃，理论上远远高于铜的熔点(1083.4℃)。因此可将铜电极置于点坐标(7.5, 20)进行微波加热，并可适当缩短加热时间及降低磁控管输入功率以提高微波能利用率，减少能耗，以达到理想的加热效果。另外，比较图7和图3(b)发现二者的数值分布规律相吻合，进一步证明Q_sh为铜电极的热源。

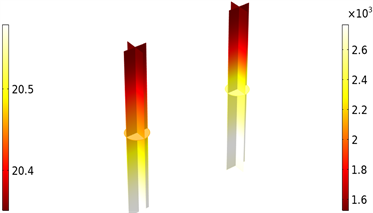
Figure 8. Temperature field of copper electrode at (7.5, 20) and (19, 1.5)

图8. 处于(7.5, 20)和(19, 1.5)时铜电极的温度场

基于平均温度与加热位置的分布关系，图8进一步给出t = 1.5 min时加热效率最高的点坐标(7.5, 20)和加热效率最低的点坐标(19, 1.5)的多切面温度场对比图。可以看到，二者的数值范围存在极大差异，而且平均温度越高，温度梯度越明显。

5.2. $\left|S_{11}\right|$

S参数(即散射参数)描述了电磁波在滤波器、天线、波导转换和传输线等设备的不同端口上的传输和反射。它来源于传输线理论，由发射和反射电压波定义。如果存在两个端口，并分别以数字1和2表示，端口1是入口，则S₁₁为端口1处的电压反射系数，S₂₁为端口1至端口2处的电压传输系数。或者说S₁₁是反射波的S参数，S₂₁是透射波的S参数。为了方便，S₁₁使用以下关系式表出 [8]：

$S_{11dB}=20{\log }_{10}\left|S_{11}\right|$ (4.2.1)

式中 $\left|S_{11}\right|$ 为端口反射系数， $S_{11dB}$ 表示回波损耗。

因为本模型只有一个输入功率为500 W的端口，故只引用 $\left|S_{11}\right|$ 衡量铜电极对端口馈入电磁波的反射程度。通过全局计算可得到谐振腔内一系列的 $\left|S_{11}\right|$ 值，结果如图9所示。 $\left|S_{11}\right|$ 范围在0.799~1，表明铜电极对端口馈入的电磁波反射程度普遍较大，甚至会出现全反射的现象。

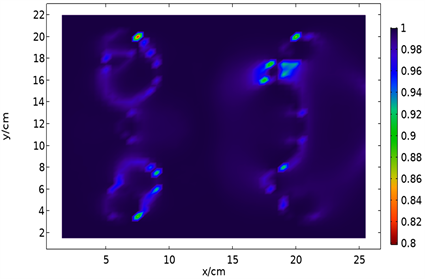
Figure 9. Numerical distribution of $\left|S_{11}\right|$ in xy plane

图9. $\left|S_{11}\right|$ 在xy平面的数值分布

如果将铜电极置于反射系数较大的坐标点进行加热，不仅会大幅度地降低微波加热效率，而且过大的反射能量会损坏端口(微波源)，这将引发安全问题和造成不必要的财产损失。所以，通过数值仿真得到合理的结果，对实验研究和理论分析具有一定指导作用，能够弥补实验工作上的不足，有效减少实验次数和压缩实验成本，可达到预设的实验效果。

5.3. 平均温度与 $\left|S_{11}\right|$ 、Q_sh的关系

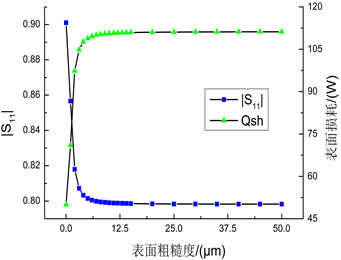
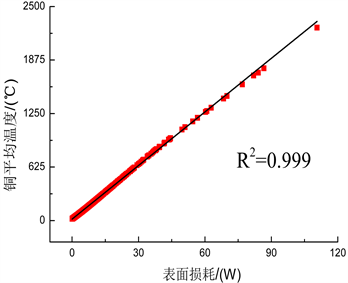
我们发现，图9， $\left|S_{11}\right|$ 分布规律与图3(b)及图7相吻合。为了进一步说明三者之间的具体关系，图10给出了铜电极平均温度与Q_sh、 $\left|S_{11}\right|$ 的散点图。可以看出，图10(a)回归拟合效果很好，图10(b)平均温度在相对较低的范围内与 $\left|S_{11}\right|$ 近似满足线性关系。因此可以认为Q_sh与平均温度呈正相关关系，而 $\left|S_{11}\right|$ 与平均温度呈负相关关系。显然，Q_sh与 $\left|S_{11}\right|$ 对于铜电极温度而言是一对互补参数，电磁波反射程度越大，那么必然导致电磁损耗减少，则铜电极平均温度越低。

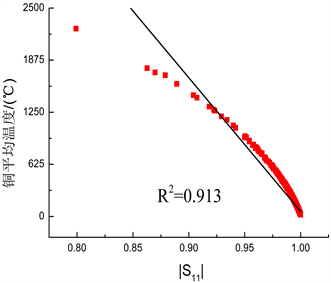(a) (b)

Figure 10. Scatter diagram of mean temperature related to Q_sh and $\left|S_{11}\right|$ respectively

图10. 平均温度与Q_sh、 $\left|S_{11}\right|$ 的散点图

6. 表面粗糙度对平均温度和 $\left|S_{11}\right|$ 的影响

表面粗糙度是指材料表面上具有的较小间距的微小峰谷组成的微观几何形状特性，记ΔRMS (SI单位：m)为表面粗糙度的均方根 [8]，如图11所示。

Figure 11. Diagram of surface roughness (upside)

图11. 表面粗糙度示意图(上侧)

我们发现铜的表面粗糙度亦会影响其温度，保持加热时间、输入功率、微波频率、加热位置(7.5, 20)不变，研究表面粗糙度0~50 μm时铜电极平均温度的变化。由式(3.5)得， $Q_{sh}$ 与 ${{\epsilon }^{″}}_r$ 、 $k^{″}$ 、 $\left|E_{t,i}\right|$ 有关。所以，为了探究温度和表面粗糙度之间的关系，我们分别计算了以上三个参数和表面粗糙度的关系。同时考虑到电场分布的不均匀性，故使用其平均值来代替局部场强大小。图12依次给出了三者和表面粗糙度的关系。

(a) (b) (c)

Figure 12. Relations between ${{\epsilon }^{″}}_r$, $k^{″}$, $\left|E_{t,i}\right|$ and surface roughness respectively

图12. ${{\epsilon }^{″}}_r$ 、 $k^{″}$ 、 $\left|E_{t,i}\right|$ 与表面粗糙度的关系

从关系图可以看到，三者随粗糙度的变化始终是连续的。就 $\left|E_{t,x}\right|$ 和 $\left|E_{t,y}\right|$ 而言，两者具有良好的一致性，场强均接近0且受粗糙度影响极小，故在相同粗糙度范围内 $\left|E_{t,z}\right|$ 对Q_sh的影响比其他两个电场分量要大得多，因此可忽略它们对Q_sh的贡献。进一步地来说，粗糙度对 ${{\epsilon }^{″}}_r$ 、 $k^{″}$ 、 $\left|E_{t,z}\right|$ 的影响既有共性又有特性。具体表现为： ${{\epsilon }^{″}}_r$ 、 $k^{″}$ 、 $\left|E_{t,z}\right|$ 在0~10 μm均发生突变，而在10~50 μm内可看作是相对平缓的有界线段，几乎不受粗糙度的影响。但是各自的单调性却截然不同， ${{\epsilon }^{″}}_r$ 和 $k^{″}$ 在0~10 μm急剧递减，而 $\left|E_{t,z}\right|$ 在上述相同区间下急剧递增。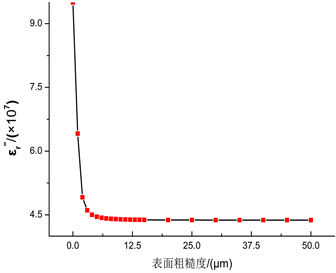比较和分析三者的变化趋势以及变化相对幅度，综合式(3.5)可推出Q_sh在0~10 μm理应急剧递增，而在10~50 μm相对平缓，整体的变化规律和 $\left|E_{t,z}\right|$ 是相类似的。通过进一步的计算可以验证，如图13(a)所示。又因为 $\left|S_{11}\right|$ 与Q_sh是一对互补参数，因此 $\left|S_{11}\right|$ 随粗糙度的变化趋势必然与Q_sh相反。

(a) (b)

Figure 13. Relations between Q_sh, $\left|S_{11}\right|$, mean temperature and surface roughness respectively

图13. Q_sh、 $\left|S_{11}\right|$ 、平均温度与表面粗糙度关系

确定了Q_sh和表面粗糙度的关系后，根据式(2.10)不难推导出铜电极平均温度与表面粗糙度之间的关系，可通过进一步的计算得到验证，结果如图13(b)所示。具体表现在当表面粗糙度为0~10 μm时平均温度急剧递增，从973.96℃增加至2250℃。而在10~50 μm时温度平缓变化，稳定在2250℃~2264℃之间。可见与光滑表面相比，粗糙度的存在有利于铜电极升温，但从结果上来看它对温度的影响还是有一定局限性的。

除此之外，我们还进一步研究了铜电极的温度场与表面粗糙度的关系。由于在低粗糙度的条件下铜电极的平均温度变化较为明显，因此图14给出了六个具有代表性且对应于不同粗糙度下铜电极的温度场。

(a) 0 μm (b) 1 μm (c) 2 μm (d) 3 μm (e) 4 μm (f) 5 μm

Figure 14. Temperature field of copper electrode with surface roughness of 0, 1, 2, 3, 4, 5 μm

图14. 表面粗糙度0、1、2、3、4、5 μm铜电极的温度场

7. 结论

本文通过COMSOL Multiphysics建立一个铜电极和谐振腔的电磁传热双向耦合模型，研究了加热位置和表面粗糙度对铜电极平均温度的影响。仿真结果表明，各位置点的平均温度差异较大，最小仅比室温高0.469℃，而最高可达2253℃，表明位置是获得高温的关键。此外，铜的表面粗糙度亦会影响其加热效果。计算表面粗糙度为0~50 μm铜电极的平均温度，发现0~10 μm时温度会发生突变并升高至2250℃，随后几乎不受粗糙度影响，温度稳定在2250℃~2264℃之间。由位置变化引起温度的改变是不连续的，跳跃的，而由表面粗糙度变化引起温度的改变是连续的，单调的。

基金项目

广东省普通高校特色创新类项目(419N05)。

参考文献

NOTES

^*通讯作者。