1. 引言
高考不仅是一场考试,更是莘莘学子人生中的重大转折点,是我国选拔人才、保证公平公正的重要参照指标。正因如此,国家不断进行高考改革和优化,旨在实现一个公平公正的评价环境,培养全方面发展的中国公民。
自2015年山东、江西和辽宁三省取消自主命题,统一采用全国卷后,各个省份纷纷加入到全国卷的“阵营”里来,而现如今,第三批高考综合改革已经在一些省份开展的如火如荼,江苏省就是其中之一。2019年4月23日,江苏省发布高考新方案,方案中指出高考考生最终总分的组成部分为:统一高考的语文、数学、外语科目成绩和学业水平考试3门选择性考试科目。从新方案中,我们可以获悉:数学学科将不再由江苏本省自主命题,而是回归全国高考,统一采用全国卷。全国卷和江苏卷之间,无论是题型结构还是综合难度等均存在差异,这对已经适应多年江苏卷的教师来说是一个巨大的挑战,为应对新高考改革,教师必须改变未来的教学方法和侧重点。本文以此为切入点,基于对全国卷和江苏卷之间的对比研究,希望为各位教师的教学带来启示。
本研究将从考察内容、能力要求、整体难度三个方面横纵向比较2015年至2019年全国I卷(理)与江苏卷(理)数学试题的异同,从而得出结论。
2. 研究设计
2.1. 研究对象
鉴于全国I、II、III卷的差别不大,本文取近五年(2015~2019年)全国I卷(理)和江苏卷(理)为研究对象。
2.2. 研究工具
2.2.1. 考察内容的分类
通过查阅高考大纲和新课标、研读高中数学教科书,将数学学科高考考察内容分为以下十个知识单元:集合与逻辑用语、函数与导数、三角函数、向量、数列、不等式、立体几何、平面解析几何、概率与统计和其他。每个知识单元含有多个知识点,具体见表1:

Table 1. Classification of investigation contents
表1. 考察内容的分类
2.2.2. 能力要求的分类
任子朝等人 [1] 对旧考纲的能力结构进行了重新整合,调整为空间想象能力、逻辑思维能力、运算求解能力、数据处理能力和创新应用能力,能力层次和对应的能力要求具体见表2:


Table 2. Classification of competence requirements
表2. 能力要求的分类
2.2.3. 整体难度的框架
本部分的研究主要参照了鲍建生的综合难度模型 [2] [3] 以及武小鹏改编的评价模型 [4],武小鹏在鲍建生的综合难度基础上,将整体难度扩充为七个维度:背景因素、是否含参、运算水平、推理能力、知识含量、思维方向、知识水平。其中,把运算水平分为了四个层次:简单数值运算、复杂数值运算、简单符号运算、复杂符号运算,而在统计过程中发现有不少无运算的试题出现。因此,我们仍采用鲍建生对运算水平的层次划分:无运算、数值运算、简单符号运算、复杂符号运算。各维度的层次水平及其对应编码见表3:

Table 3. Framework of overall difficulty
表3. 整体难度的框架
依据上表的综合难度系数框架,可以建立各因素的难度系数模型
其中i表示不同的维度,
为第i个维度中的第j个水平的权重(依据不同水平分别取
),
则表示这组题目中属于第i个维度中的第j个水平的题目的个数,n代表题目的总个数。
统计过程中作如下规定:1) 将复数的运算归为数值运算;2) 一个题目中如果既包含数值运算也包含符号运算,一律按符号运算处理,无论出现了多少步数值运算统一记为1步运算;3) 简单加减乘除不计入数值运算,如1 + 1 = 2;4) 同样思维的反复推理仅算一步推理,比如算法框图里的循环结构;5) 解答题中各维度的层次水平以各小问的平均值来归类;6) 思维方向既有正向也有逆向时取逆向。
2.3. 数据处理与整理
为更好地理解研究工具,界定试题考察内容、能力要求、整体难度各因素水平的分类,以2019年全国I卷中的一道试题为例进行说明:
(2019年全国I卷,1)已知集合
,
,则
( )
A.
B.
C.
D.
考察内容:集合与逻辑用语,不等式。
能力要求:逻辑思维能力,运算求解能力。
整体难度:无背景,有参数(含x),简单符号运算(解不等式和集合交运算,共2步运算),简单推理(先确定集合N,再计算
,共2步推理),两个知识点(集合与逻辑用语,不等式,共2个知识点),顺向思维,运用(集合和不等式的综合运用)。
3. 研究结果与分析
3.1. 考察内容的比较与分析
根据考察内容的分类,数学学科的考试内容可以分为集合与逻辑用语等十大类。需要说明的是:高考试题侧重于对知识点的综合考察,因此必然会有一些知识交汇题目(一题涉及多个知识点)的出现,统计分值时,我们根据知识点的个数将题目对应分值平分;鉴于全国卷和江苏卷的总分不同、题型不同、各题对应分值也不同,本部分分析的指标设为考察内容所占分值与总分值的比值
;两种试卷类别的选做题除内容外难度差异不大、形式固定,所以本次研究未将选做题纳入统计范围,即全国卷总分值为140分,江苏卷总分值(含必做题)为180分。易知
,
统计结果见表4:


Table 4. The proportion of each knowledge unit in the national volume and Jiangsu volume from 2015 to 2019
表4. 2015~2019年全国卷与江苏卷考察内容各知识单元的占比
为更好的观察和比较,绘制折线图如下,见图1、图2、图3、图4、图5:
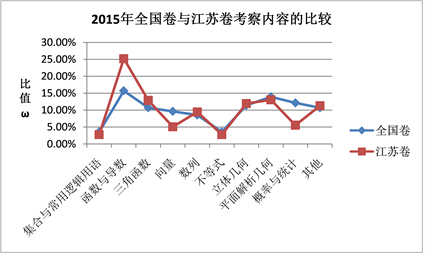
Figure 1. Broken line chart of the proportion of each knowledge unit in 2015 national volume and Jiangsu volume
图1. 2015年全国卷与江苏卷考察内容各知识单元占比折线图

Figure 2. Broken line chart of the proportion of each knowledge unit in 2016 national volume and Jiangsu volume
图2. 2016年全国卷与江苏卷考察内容各知识单元占比折线图
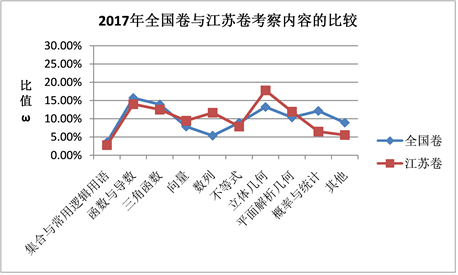
Figure 3. Broken line chart of the proportion of each knowledge unit in 2017 national volume and Jiangsu volume
图3. 2017年全国卷与江苏卷考察内容各知识单元占比折线图
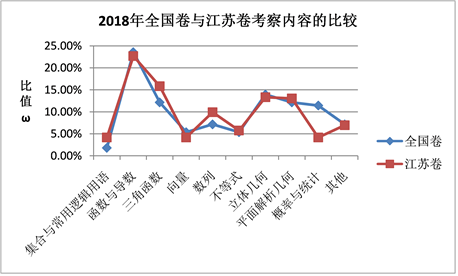
Figure 4. Broken line chart of the proportion of each knowledge unit in 2018 national volume and Jiangsu volume
图4. 2018年全国卷与江苏卷考察内容各知识单元占比折线图
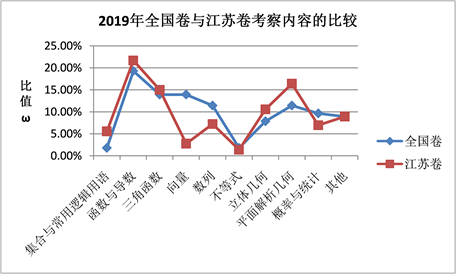
Figure 5. Broken line chart of the proportion of each knowledge unit in 2019 national volume and Jiangsu volume
图5. 2019年全国卷与江苏卷考察内容各知识单元占比折线图
根据对全国卷和江苏卷的考察内容分析,能够得出以下结论:
1) 江苏卷集合与常用逻辑用语、函数与导数、三角函数、立体几何相比全国卷总体偏多,全国卷向量、概率与统计、其他相比江苏卷总体偏多,不等式差距不大,数列、平面解析几何无规律;
2) 全国卷立体几何一般与空间向量联系在一起综合考察;
3) 全国卷集合与常用逻辑用语、数列、其他均以基础小题(选择题或填空题)呈现,江苏卷有时会以解答题甚至压轴题出现;
4) 全国卷各内容分值占比相对江苏卷较均衡、考察较全面,二者解答题题型固定,但考察内容不尽相同:全国卷解答题(17~21)的考察内容一般固定为:三角函数、立体几何、概率与统计、平面解析几何、导数与函数五大部分;江苏卷I卷中解答题(15~20)的考察内容一般分为三角函数、立体几何、实际应用题(涉及立体几何、函数与导数、平面解析几何等的综合应用题)、平面解析几何、函数与导数、数列六大部分,II卷中必做题(22~23)考察内容并不固定;
5) 全国卷着重对函数与导数、平面解析几何、三角函数的考察,其对应分值占比ω五年来(2016~2019年)均位列前5。
3.2. 能力要求的比较与分析
根据研究工具中任子朝等对数学能力进行整合后的结构分类,数学学科的能力要求可分为空间想象能力等五大能力。与考察内容的统计方法一样,当出现能力交汇的题目(一题涉及多个能力要求)时,根据能力要求的个数将题目对应分值平分;本部分分析的指标设为能力要求所占分值与总分值的比值
;本次研究未将选做题纳入统计范围,即全国卷总分值为140分,江苏卷总分值(含必做题)为180分。易知
,
统计结果见表5:

Table 5. Proportion of capacity requirements of national volume and Jiangsu volume in 2015~2019
表5. 2015~2019年全国卷与江苏卷各能力要求的占比
为更好的观察和比较,绘制折线图如下,见图6、图7、图8、图9、图10:
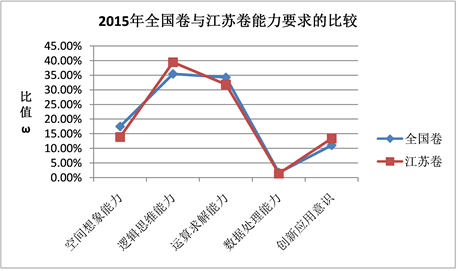
Figure 6. Broken line chart of the proportion of capacity requirements of national volume and Jiangsu volume in 2015
图6. 2015年全国卷与江苏卷各能力要求占比折线图
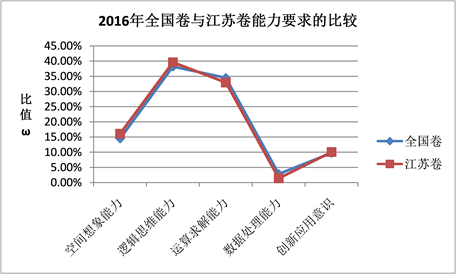
Figure 7. Broken line chart of the proportion of capacity requirements of national volume and Jiangsu volume in 2016
图7. 2016年全国卷与江苏卷各能力要求占比折线图
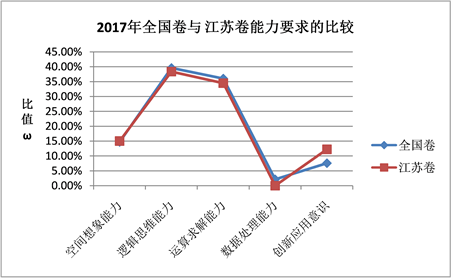
Figure 8. Broken line chart of the proportion of capacity requirements of national volume and Jiangsu volume in 2017
图8. 2017年全国卷与江苏卷各能力要求占比折线图

Figure 9. Broken line chart of the proportion of capacity requirements of national volume and Jiangsu volume in 2018
图9. 2018年全国卷与江苏卷各能力要求占比折线图
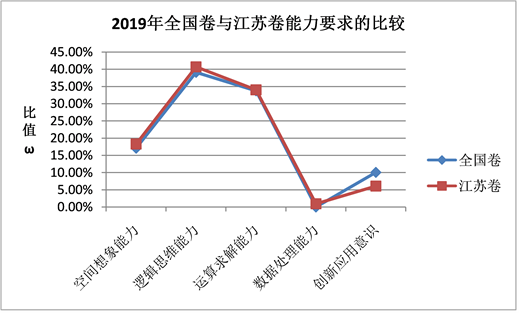
Figure 10. Broken line chart of the proportion of capacity requirements of national volume and Jiangsu volume in 2019
图10. 2019年全国卷与江苏卷各能力要求占比折线图
根据对全国卷和江苏卷的能力要求分析,能够得出以下结论:
1) 江苏省逻辑思维能力的占比更高,相比全国卷更注重逻辑思维能力的考察;
2) 全国卷空间想象能力、运算求解能力、数据处理能力的占比更高,相比江苏卷更注重这三方面能力的考察;
3) 二者逻辑思维能力和运算求解能力占试卷总分值比例均较大,且所有能力要求的对应分值占比排序相同:逻辑思维能力 >= 运算求解能力 > 空间想象能力 > 创新应用意识 > 数据处理能力。
3.3. 整体难度的比较与分析
本部分的研究主要参照了鲍建生的综合难度模型以及武小鹏改编的评价模型,将整体难度分为背景因素等七个维度。并计算出对应的难度系数模型
(加权平均值),统计结果见表6:

Table 6. The difficulty coefficient model of each difficulty factor of the overall difficulty of national and Jiangsu papers in 2015~2019
表6. 2015~2019年全国卷与江苏卷整体难度各难度因素的难度系数模型
为更好的观察和比较,绘制雷达图如下,见图11、图12、图13、图14、图15:
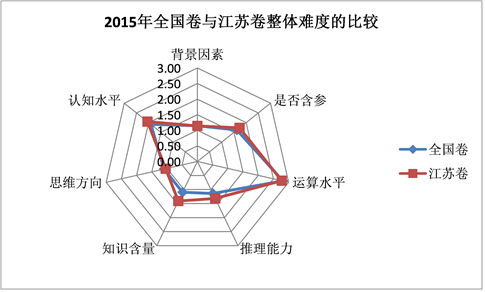
Figure 11. Radar chart of overall difficulty of national volume and Jiangsu volume in 2015
图11. 2015年全国卷与江苏卷整体难度雷达图

Figure 12. Radar chart of overall difficulty of national volume and Jiangsu volume in 2016
图12. 2016年全国卷与江苏卷整体难度雷达图
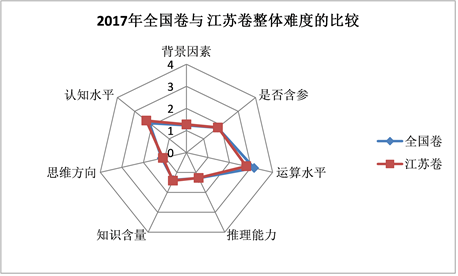
Figure 13. Radar chart of overall difficulty of national volume and Jiangsu volume in 2017
图13. 2017年全国卷与江苏卷整体难度雷达图

Figure 14. Radar chart of overall difficulty of national volume and Jiangsu volume in 2018
图14. 2018年全国卷与江苏卷整体难度雷达图

Figure 15. Radar chart of overall difficulty of national volume and Jiangsu volume in 2019
图15. 2019年全国卷与江苏卷整体难度雷达图
根据对全国卷和江苏卷的整体难度分析,能够得出以下结论:
1) 全国卷运算水平普遍偏高,江苏卷推理能力、知识含量普遍偏高,背景因素、是否含参、思维方向总体差距不大,认知水平无明显规律;
2) 江苏卷整体难度与全国卷差异不大。
3.4. 研究结果
1) 全国卷知识内容的侧重程度和考察形式与江苏卷有一些差异。
2) 根据统计结果:全国卷运算水平普遍偏高,全国卷运算求解能力的占比更高,因此全国卷较江苏卷更加注重运算求解能力的考察。
3) 能力考查的分析中发现全国卷空间想象能力要求普遍高于江苏卷,这说明全国卷较江苏卷更加注重空间想象的考察。
4) 全国卷和江苏卷都注重基础知识和主干内容的考察。
4. 教学建议
根据以上的数据及结论,笔者在这里为教师提出几点教学建议,以适应新高考的要求:
1) 进行教学调整,教学内容可以有所侧重
全国卷内容分布相比江苏卷均衡,每个知识单元都尽量会有所涉及,题型固定,如解答题一般分为:三角函数、立体几何、概率与统计、平面解析几何、导数与函数五大部分,因此,教师可以对这些内容进行专题教学或复习;同时课本上每一个知识点都应该重视,不要有“漏网之鱼”;
立体几何有关二面角、面面垂直等问题一般可以通过建系用空间向量解决,使得一些题目思路固定、逻辑清晰,属于简单题,在这一部分的练习需要加强学生的运算能力,只要细心,此类题型得分较为容易;
概率与统计需要引起重视,根据结论,全国卷中必有一道概率与统计的应用题出现,因此,必须培养学生将实际生活问题转化成数学问题的能力,提高阅读能力、理解能力,运用创新的意识和创新的能力;
数列的考察不像江苏卷,几乎以基础小题为主,一般只要熟记公式、掌握等差数列与等比数列的基本概念和性质就容易得分,但对于学有余力的同学,依然可以指导继续深入;
不等式差距不大,教学可不作调整;
两种试卷类型中函数与导数永远占据最高的比例,应继续予以重视。
2) 注重运算求解能力的培养
教师应加强学生的运算求解能力,培养学生运算速度和质量,并且多教授创新灵活的运算技巧使得问题更加简单;少做偏题怪题技巧性强的题,多做一般化题型。教学中运算求解能力的培养需要注意以下几点:
① 注重公式等一系列运算基础知识和能力的教学;
② 传授灵活的运算技巧,锻炼学生用宏观的视角看待运算对象,有时候看似繁琐的运算其实只需几步变形或换元就能变为简单的运算,要求学生敏锐地捕捉到式中隐藏的关系和条件,需要一定程度和规模的训练;
③ 注意符号运算能力的培养;
④ 展示典型例题的过程示范,明晰一般步骤及其对应的依据,这样可使学生养成规范的运算习惯和清晰的运算思路,这对于解决一般难度的试题有着很显著的作用,同时也能大大地提高运算的准确率;
⑤ 督促学生养成验算和检查的良好习惯,提高运算合理性和精确性,学生在运算过程中容易粗心,因此要特别强调验算的重要性,做到每一步有理、每一环有据,精力集中、认真演算,切忌想当然。
3) 注重空间想象能力的培养
广义的来说,空间想象能力不仅体现在狭义的几何板块如立体几何和解析几何,也体现在数形结合,读图识表等方方面面,这就需要教师在日常教学中渗入“图形”的思想,鼓励学生多用图像结合题意解题、借助几何画板等教学工具直观地帮助学生理解等等。空间想象能力的培养尤其在函数、统计、几何等相关问题的求解中起到至关重要的作用。
4) 注重基础知识和主干内容的教学
研究产生了一个有趣的结论,素来有“地狱模式”之称的江苏高考数学,实际上,整体难度与全国卷差异不大。通过对数据的深入研究,可以发现江苏卷的试题总体上更加偏向知识的综合应用以及学生逻辑思维能力的考察,全国卷虽然在这两方面要求较低,但对运算水平要求较高,一定程度上提高了整体难度。
无论是全国卷还是江苏卷,它们的认知水平均以理解和运用为主,也就是说,整个卷面大多数是基础题和中档题,这就表明在教学过程中,教师一定要注意对主干内容和基础知识的教学,帮助学生吃透教材,善于使用思维导图,建构一个庞大的、清晰的知识网络体系。