蜂窝陶瓷换热器的预热特性

Preheating Characteristics of Honeycomb Ceramic Heat Exchanger

摘要: 针对高温烟气和空气通过堆积蜂窝陶瓷蓄热体的换热过程，基于单孔蓄热体模型，通过数值模拟研究了流速和换向时间对预热过程中流体温度、蓄热体温度的演变过程，以及换热稳定后所达温度效率的影响。结果表明，在高温烟气进口温度1123.15 K、空气进口温度313.15 K的条件下，当换热时间为60 s时，随着迎面风速从0.75 m/s增加到1.5 m/s，放热期末空气出口温度从1083.83 K下降到1055.05 K，温度效率从95.15%下降到91.59%；当换向时间为90 s时，随着迎面风速从0.75 m/s增加到1.5 m/s，放热期末空气出口温度从1076.25 K下降到1040.37 K，温度效率从94.21%下降到89.78%。在相同的迎面流速下，换向时间越短，蓄热期烟气出口温度越小，放热期空气出口温度和温度效率越高；在相同的换向时间下，进口流速越大，蓄热期烟气出口温度越高，放热期空气出口温度和温度效率越低。蜂窝陶瓷蓄热体中换热过程的热惰性很强，需要经历较长的时间才能趋于稳定。

Abstract: Aiming at the heat exchange process of high-temperature flue gas and air passing through the stacked honeycomb ceramic regenerator, based on the single-hole regenerator model, numerical simulations were carried out to study the effects of flow velocity and switching time on the tem-perature distribution of fluid and honeycomb ceramics during the preheating process, and the ef-fect on the temperature efficiency reached after the heat exchange was stabilized. The results show that under the conditions of high temperature flue gas inlet temperature 1123.15 K and air inlet temperature 313.15 K, when the switching time is 60 s, as the face velocity increases from 0.75 m/s to 1.5 m/s, the air outlet temperature at the end of heat release period changes from 1083.83 K to 1055.05 K, and the temperature efficiency drops from 95.15% to 91.59%, when the switching time is 90 s, as the face velocity increases from 0.75 m/s to 1.5 m/s, the air outlet temperature at the end of heat release period drops from 1076.25 K to 1040.37 K, and the temperature efficiency drops from 94.21% to 89.78%. Under the same face velocity, the shorter the switching time, the lower the flue gas outlet temperature during the heat storage period, and the higher the air outlet temperature and temperature efficiency during the heat release period. Under the same switching time, when the inlet flow rate increases, the flue gas outlet temperature during the heat storage period increases, and the air outlet temperature decreases during the heat release period as well as the temperature efficiency. The thermal inertia of the heat exchange process in the honeycomb ceramic regenerator is very strong, and it takes a long time to stabilize.

1. 引言

蓄热氧化技术(regenerative thermal oxidizer，RTO)是最具有发展前景的VOCS处理方法之一。蓄热氧化技术与催化燃烧、直燃式热氧化技术相比，处理大风量、中低浓度的工业有机废气效果显著。它的突出优点是可得到高达99%以上的净化效率，同时达到95%以上的热回收效率 [1]。蓄热体是蓄热式热氧化炉的关键部件，当前应用最为广泛的是蜂窝陶瓷，它具有比表面积大、换热效果好、流动阻力低等优点 [2] [3]。

欧俭平 [4] 通过建立蓄热体三维非稳态传热数学模型数值计算得到，气体流速对蓄热体的热工特性有一定影响，蓄热体在具体的工作条件下，存在一个最佳换向时间。刘永启 [5] 通过实验对莫来石蓄热体研究得到蜂窝陶瓷阻力损失随蓄热体长度增加而增大，同一蓄热体阻力损失随气体流速增加而增大，并根据实验数据得到了莫来石蜂窝陶瓷蓄热体摩擦阻力系数的实验关联式。郑志伟 [6] 等对两种规格蓄热体的实验研究表明蓄热体的阻力损失随着体积流量、比表面积的增加而增大。当孔内流速相同时，摩擦阻力损失系数与当量直径成反比。张振兴 [7] [8] 通过实验和模拟对不同孔型、壁厚、孔隙率的蓄热体进行研究得到在同一特征长度下，方形蜂窝体具有较大的比表面积，在同孔隙率、比表面积和当量直径条件下，方形陶瓷体的阻力损失较低。Yonghua You [9] 验证了数学模型的有效性，分析了蓄热室的传热机理，在不同的流体流速条件下，研究了蓄热室长度和切换时间对传热和流阻性能的影响。JEA Coutinho [10] 通过实验模拟对比对空气/甲烷流过多孔介质的研究得到较高的入口速度会导致气体温度升高。提高预热段的导热系数降低了燃烧区的峰值温度。在燃烧区使用导热系数很高的多孔材料对燃烧区的温度水平没有显著影响。李伟等 [11] 模拟计算了蓄热过程和放热过程的烟气和空气温度和速度的变化情况，以及气流速度和材料比热对蓄热体性能的影响。

目前，关于蓄热体传热和阻力特性的研究大多是针对单个蓄热体 [12] [13] [14] [15]。考虑到工程应用中蓄热体是在堆积状态下工作的，蓄热体中气体温度通常不是线性分布，且存在周期性变化，与流动速度和流动阻力也有交互影响，针对单个蓄热体的研究结果较难直接用于指导工程设计。目前在蓄热氧化炉的蓄热室设计中，尚难以通过简单的计算获得可靠的热工性能参数，并掌握其动态特性，实验研究时间长，测试也比较复杂。因此，本文针对高温烟气和空气通过堆积蜂窝陶瓷蓄热体的换热问题，通过数值模拟研究流速和换向时间对预热过程中流体温度、蓄热体温度的演变过程，以及换热稳定后所达温度效率的影响，为工程应用提供参考。

2. 模型简介

2.1. 物理模型

图1是某蓄热氧化炉的一个蓄热室中蜂窝陶瓷的堆积状态示意图。蓄热体规格为150 mm × 150 mm × 300 mm、40 × 40孔的堇青石材质蜂窝陶瓷，方孔尺寸为3 mm × 3 mm，壁厚0.7 mm，孔隙率为0.64，共堆积5层，总高度1.5 m。

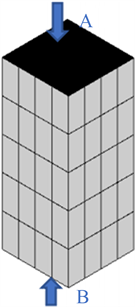
Figure 1. Schematic diagram of accumulation state of regenerator

图1. 蓄热体堆积状态示意图

在蓄热氧化炉运行过程中，蜂窝陶瓷蓄热体本质上是一个蓄热式热交换器，它的一个换热周期包括蓄热和放热两个阶段。在蓄热期，高温烟气从A端流入，蓄热体吸收烟气热量，冷却后的烟气从B端排出；在放热期，常温的挥发性有机物废气从B端流入，蓄热体释放热量预热废气，加热后的废气从A端流出进入燃烧室。在蓄热期和放热期，冷热流体的质量流量相等。本文主要关注蓄热体回收烟气热量预热废气的效果，暂不考虑蓄热体中挥发性有机物的燃烧。

2.2. 网格划分

由于每个蓄热体由多个相同形状的孔道组成，假定气流通过蜂窝陶瓷各孔的流速均匀，每个通道的传热情况一致，可将其简化为一个孔道加四周二分之一的壁厚作为单孔模型进行数值模拟研究。图2为单孔模型的网格划分，方孔边长3 mm，四周的壁厚0.35 mm，高1.5 m。网格划分采用六面体结构化网格，网格尺寸0.25 mm，网格总数2,496,832。

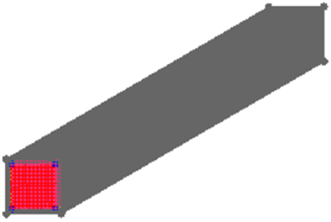
Figure 2. Three dimensional single hole mesh model of stacked honeycombs

图2. 堆积蜂窝体三维单孔模型的网格划分

2.3. 数学模型

蜂窝陶瓷蓄热体与气体介质之间传热的数学模型是建立在能量、质量和动量三大守恒方程基础上的。蓄热体与流体的温度变化是关于时间t和位置(x, y,z)的函数。在建立数学模型时作以下假设：

1) 高温烟气或空气流入蓄热体的温度和流速在入口界面上是均匀的；

2) 蓄热体的表面积及质量分布是均匀的；

3) 换向瞬间完成。

流体的质量守恒方程为：

$\frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho u\right)}{\partial x}+\frac{\partial \left(\rho v\right)}{\partial y}+\frac{\partial \left(\rho w\right)}{\partial z}=0$ (1)

式中，ρ为流体的密度，t为时间，u、v和w分别是x、y和z方向的速度。

流体的动量方程为：

$\frac{\partial \left(\rho u\right)}{\partial t}+div\left(\rho uu\right)=-\frac{\partial p}{\partial x}+\frac{\partial {\tau }_{xx}}{\partial x}+\frac{\partial {\tau }_{yx}}{\partial y}+\frac{\partial {\tau }_{zx}}{\partial z}+F_x$ (2)

$\frac{\partial \left(\rho v\right)}{\partial t}+div\left(\rho vu\right)=-\frac{\partial p}{\partial y}+\frac{\partial {\tau }_{xy}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}+\frac{\partial {\tau }_{zy}}{\partial z}+F_y$ (3)

$\frac{\partial \left(\rho v\right)}{\partial t}+div\left(\rho wu\right)=-\frac{\partial p}{\partial z}+\frac{\partial {\tau }_{xz}}{\partial x}+\frac{\partial {\tau }_{yz}}{\partial y}+\frac{\partial {\tau }_{zz}}{\partial z}+F_z$ (4)

式中，u为速度矢量，u、v和w是u在x，y和z方向的速度分量；p为作用在流体上的压力；τ是粘性应力，τ_xx、τ_xy和τ_xz等分别是作用在微元体表面的粘性应力τ的分量；而F_x、F_y和F_z是作用于微元体x、y、z方向上的质量力。

流体的能量守恒方程为：

$\frac{\partial \left(\rho T\right)}{\partial t}+div\left(\rho uT\right)=div\left(\frac{k}{c_p}grad|T\text{}\text{}\right)+S_T$ (5)

式中，c_p为定压比热容，T为温度，k为流体的导热系数，S_T为单位体积流体的内热源与由于粘性作用流体机械能转换为热能之和。

固体的能量守恒方程为：

$\frac{\partial \left({\rho }_s{T}_s\right)}{\partial t}=div\left(\frac{k_s}{c_{p,s}}grad\text{}\text{}|T_s\right)+S_{T,s}$ (6)

式中， ${\rho }_s$ 为固体的密度， $c_{p,s}$ 为固体的比热容， $T_s$ 为固体的温度， $k_s$ 为固体的导热系数， $S_{T,s}$ 为单位体积固体的内热源。

2.4. 参数设置

蜂窝陶瓷为致密堇青石，密度为2420 kg/m³，比热容为942 J/(kg K)，导热系数为1.89 W/(m·K)。孔道内为层流流动，外壁面为绝热，内壁面为流固耦合传热。用Fluent日志文件实现周期性换向，蓄热期和放热期的时间相等，即换热周期为换向时间的两倍。换向时间分别为60 s和90 s。边界条件为质量入口和自由流出边界条件。冷流体从B侧流入时的空截面流速定义为迎面流速，迎面流速u的变化范围0.75~1.5 m/s，对应的单孔质量流量1.19 × 10⁻⁵~2.38 × 10⁻⁵ kg/s，与热流体从A侧流入时的质量流量相等。冷热流体的进口温度分别为313.15 K和1123.15 K；蓄热体的初始温度为313.15 K。考虑到挥发性有机物废气的成分以空气为主，其它挥发性有机物的体积分数一般小于1%，故冷热流体的物性参数都近似采用空气的物性参数，为表述方便，将冷流体称为空气，热流体称为烟气。具体的模拟工况参数如表1所示。

Table 1. Parameters of simulated working conditions

表1. 模拟工况参数

3. 预热过程中气体温度分布的演变

各工况下蜂窝陶瓷蓄热体的初始温度为313.15 K，随着高温烟气和空气周期性交替进入蓄热体，蓄热体被逐步预热，空气出口温度不断上升，最后趋于稳定。以工况1为例，当换向时间60 s，迎面流速0.75 m/s时，蓄热期末沿蓄热体高度方向烟气温度分布的演变如图3所示。

从图3中可以看出，在预热过程中的每一个蓄热期，1123.15 K的高温烟气从蓄热体顶端流入，顶部的蓄热体最先被加热，温度迅速升高，随着烟气向下流动，烟温和蓄热体的温度都逐渐降低。随着预热过程的持续进行，蓄热体内高温区不断向下扩展，蓄热体平均温度不断提高，但底端蓄热体温度和烟气出口温度上升很缓慢。如图4所示，从1 min到477 min，烟气出口温度仅从313.15 K增加到了340.75 K。

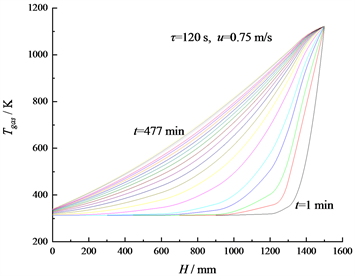
Figure 3. Evolution of flue gas temperature distribution at the end of endothermic periods

图3. 蓄热期末烟气温度分布的演变

Figure 4. Flue gas outlet temperature at the end of endothermic periods

图4. 蓄热期末烟气出口温度变化过程

在工况1条件下，放热期末蓄热体内空气温度分布的演变如图5所示。从图中可以看出，在预热过

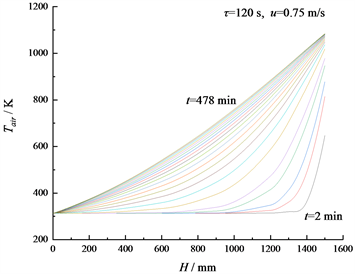
Figure 5. Evolution of air temperature distribution at the end of exothermic periods

图5. 放热期末空气温度分布的演变

程中的每一个放热期，313.15 K的空气从蓄热体底端流入，被蓄热体加热，温度逐渐升高。在第一个放热期末(t = 2 min)，空气出口温度为647.10 K。在第239个放热期末(t = 478 min)，空气的出口温度提高到T_air,max = 1083.88 K，换热已趋于稳定。从图6中可以看出，在预热过程的初期，空气出口温度迅速上升；随着预热过程的持续进行，空气出口温度继续提高，但升温速率显著减小。放热期末空气出口温度达到T_air,max的90.2%，即978.27 K，历时30 min；放热期末空气出口温度达到即1037.03 K，历时86 min；放热期末空气出口温度达到T_air,max的98.7%，即1069.86 K，历时长达226 min。可见，蜂窝陶瓷蓄热体中换热过程的热惰性很强，需要经历较长的时间才能趋于稳定，这也意味着蓄热氧化炉对运行调节的响应速度会比较慢。

Figure 6. Air outlet temperature at the end of exothermic periods

图6. 放热期末空气出口温度变化过程

4. 预热过程中蓄热体的温度分布

图7所示为换热周期保持120 s不变，不同的迎面流速下，第239个蓄热期末(t = 477 min)和放热期末(t = 478 min)蜂窝陶瓷温度T_s沿高度方向的分布规律。不同工况下蓄热体的温度分布演变过程，与烟气和空气温度分布的演变过程相似，蓄热体和烟气、空气间的传热温差很小。相同的换向周期下，随着迎面流速的增加，烟气和蓄热体的换热增强，蓄热体的升温速率也会增大。由图7(a)可以看出，流速越高时蓄热体在蓄热期末的温度水平越高。由图7(b)可以看出，放热期时流速对整体蓄热体的温度影响主要体现在空气出口段，流速越高时放热期末的蓄热体顶端温度越低。

(a) t = 477 min 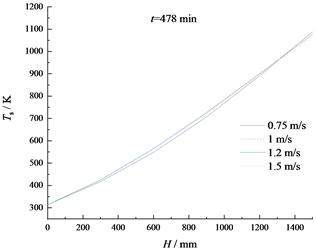(b) t = 478 min

Figure 7. Temperature distribution of honeycomb ceramics under different face velocity

图7. 不同迎面流速下蜂窝陶瓷的温度分布

图8所示为迎面流速保持1.2 m/s不变，换热周期120 s时，第239个蓄热期末(t = 477 min)和放热期末(t = 478 min)蜂窝陶瓷的温度分布，以及换热周期180 s时，第159个蓄热期末(t = 475.5 min)和放热期末(t = 477 min)蜂窝陶瓷的温度分布。在相同迎面流速下，经过相同的预热时间后，换向时间越短，蓄热体的蓄热期末温度越低，放热期末温度越高。

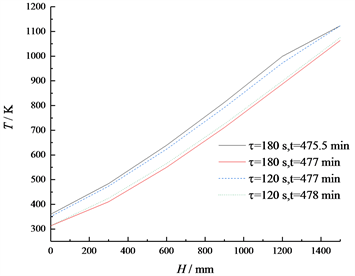
Figure 8. Temperature distribution of honeycomb ceramics under different switching time

图8. 不同换向时间下蜂窝陶瓷的温度分布

5. 堆积蜂窝陶瓷换热过程的温度效率

堆积蜂窝陶瓷换热过程趋于稳定后的温度效率是一项重要的性能参数，它反映了对高温烟气热量的回收利用程度，直接影响蓄热式氧化炉的能耗水平。在本文中，判定蜂窝陶瓷中蓄热式热交换过程达到稳定状态的标准设定为连续30 min内各放热期末空气出口温度的相对变化率小于1‰。

换热过程的温度效率ε与烟气进口温度T_gas,i、空气进口温度T_air,i、空气出口温度T_air,o的关系为：

$\epsilon =\left(T_{air,o}-T_{air,i}\right)/\left(T_{gas,i}-T_{air,i}\right).$ (7)

在一个放热期中，空气出口温度和温度效率会逐渐下降。在放热期末仍能达到所需的预热温度和温度效率，是保证蓄热氧化炉中废气充分预热和有机污染物氧化脱除的关键因素。在蓄热氧化炉设计中，通常要求蓄热体温度效率不低于0.95。不同工况下，换热过程达到稳定状态时所需时间、加热期末烟气出口温度、放热期末空气出口温度、以及按放热期末空气出口温度计算的温度效率如表2所示。

Table 2. Temperature efficiency of honeycomb ceramic heat exchange process

表2. 蜂窝陶瓷换热过程的温度效率

从表2中可以看出，在相同的换向时间下，迎面流速越高，蜂窝陶瓷换热过程的温度效率越低；在相同的迎面流速下，换向时间越短，换热过程的温度效率越高。相比之下，迎面流速对温度效率的影响更大。在所研究的8个工况中，只有在工况1条件下放热期末的温度效率仍不低于0.95。

6. 结论

本文对堇青石蜂窝陶瓷蓄热体在堆积高度为1500 mm、迎面流速为0.75~1.5 m/s、换向时间分别为60 s和90 s时的预热过程进行了数值模拟，结果表明：

1) 蓄热体预热过程中，高温烟气出口温度上升十分缓慢，上升幅度也很小；空气出口温度先急剧上升，然后升温速率迅速衰减。从蓄热体开始预热到换热过程达到稳定，所需时间均大于4小时。这表明蜂窝陶瓷蓄热体换热过程的热惰性很强，会使蓄热氧化炉对运行调节的响应速度比较慢，在蓄热氧化炉设计和运行过程中除了考虑静态特性，有必要通过数值计算进一步掌握蓄热氧化炉对气体流量、废气浓度等运行参数波动时的动态响应特性，为控制系统设计提供参考。

2) 蓄热体换热过程达到稳定以后，在相同的迎面流速下，换向时间越短，蓄热期烟气出口温度越低，放热期空气出口温度和温度效率越高；在相同的换向时间下，迎面流速越高，蓄热期烟气出口温度越高，放热期空气出口温度和温度效率越低；迎面流速对温度效率的影响比换向周期更大。

3) 在本文讨论的蓄热氧化炉常用设计参数范围内，选取迎面流速为0.75 m/s，换向时间为60 s时，在放热期末温度效率仍能达到95.15%，满足温度效率不低于95%的要求。在蓄热氧化炉设计时，应结合废气中挥发性有机物的浓度和燃点，合理选取通过蓄热体换热需要达到的温度效率和废气预热温度。废气中挥发性有机物的燃点越低，浓度和热值越高，设计选取的温度效率和废气预热温度就可以越低。在达到所需温度效率的前提下，选用较高的迎面流速，可以降低蓄热氧化炉中蓄热体的填充量、蓄热氧化炉体积和制造成本。当然，选用较高流速也会增加炉内流动阻力和运行成本，在工程设计中需要综合考虑设备投资和运行成本作进一步的技术经济分析。通过数值模拟获得的结果，可为蓄热氧化炉的热工设计提供有益的参考。

NOTES

^*通讯作者。