耦合流体动力学方程的神经网络模型研究

Neural Network Flow Field Prediction Model Coupled with Fluid Dynamics Equations

摘要: 在流体力学中应用深度学习的技术成为研究热点，但是目前使用的纯粹数据驱动的神经网络模型，不具备物理知识定律的可解释性，而且作为预测模型时，其预测准确度较差。基于此，提出了耦合物理定律的神经网络模型，以层流二维圆柱绕流为例，实现了对流体动力学方程(N-S方程)的耦合与近似求解，并对模型的短时流场预测能力进行了验证。结果表明：该模型可以使用少量的训练数据对控制方程进行近似求解，对相应已知时刻的流场进行重建；进行未知时刻流场的预测时，与相同条件下纯数据驱动的神经网络流场预测模型相比，该模型具有更小的预测误差。

Abstract: In recent years, the application of deep learning technology in fluid mechanics has become a re-search hotspot. However, currently pure data-driven neural network models do not have the inter-pretability of the laws of physical knowledge, and when used as a prediction model, its prediction accuracy is poor. Based on this, a neural network model coupled with the laws of physics was de-veloped. Taking laminar two-dimensional cylindrical flow as an example, the approximate solution of the N-S equation was achieved, and the short-term flow field prediction ability of the model was verified. The results show that the model can use a small amount of training data to approximate the governing equations and reconstruct the corresponding flow field. When predicting the flow field, the model has smaller prediction error than pure data-driven neural network model under the same conditions.

1. 引言

在工程领域，许多问题都可以归结为一个非线性过程，也即非线性方程，而数据驱动的神经网络算法具有很强的非线性建模能力，理论上可以逼近任意非线性问题的解 [1]，因此，近年来，以数据驱动的神经网络算法在各个领域得到了广泛的应用，如模式识别 [2]，自然语言处理 [3]，图像处理等 [4]。流体力学问题其本质属于非线性系统问题，借助于流体力学领域的大量高精度数据，在流体力学中应用神经网络技术成为了研究热点。使用神经网络进行流场预测的方法有两种：纯数据驱动方法；引入先验知识的耦合方法 [5]。许多研究者使用纯数据驱动神经网络方法对流体力学问题进行研究 [6]，王德明使用纯数据驱动的BP神经网络方法对风电场短期风速预测进行了研究 [7]。赵超以S形进气道为例对沿程壁面静压短时内随时间的变化进行了预测 [8]。但是纯数据驱动方法只关心神经网络输出量的准确性，不关心计算过程中的物理机理，因此该方法不仅缺少物理定律的可解释性，而且预测能力也难以保证。而引入先验知识的耦合方法不仅要求输出量的准确性，同时要求输出量满足相应的先验知识，而且引入先验知识相当于对神经网络的参数规模进行了限制，为模型增加了正则化项，可以有效提升神经网络的性能 [9]。引入先验知识的耦合方法最先由Joerding W. H.提出 [10]，并由许多领域的相关研究者进行了验证：娄海川 [11] 充分挖掘化工过程的先验知识，提出了过程先验递归神经网络，取得了良好的建模精度；周彦辰 [12] 在水质的预测应用中，以组分输运方程为例提出了一种耦合机理先验神经网络，提高了神经网络的预测以及非线性拟合能力；Raissi M. [13] [14] 以多个领域不同的非线性偏微分方程为例，提出了耦合非线性偏微分方程的深度神经网络，实现了对非线性偏微分方程的近似求解。

但是目前耦合的先验知识过于简单，包括单调性，对称性等，即便对于有明确控制方程的过程，也仅仅局限于对单一方程的耦合，而且耦合方法需要引入不必要的假设，较为繁琐，缺少对模型在未知的新数据上预测能力的验证工作。而在计算流体力学中，非线性过程所涉及到的控制方程往往包含若干个，如连续性方程，不同方向的动量方程，能量方程等 [15]，故在Raissi M.的研究基础上，本文以层流二维圆柱绕流为例，尝试将涉及的所有控制方程与神经网络进行耦合，对耦合方法进行简化，实现对控制方程进行近似求解，最后比较纯数据驱动神经网络模型和耦合控制方程的模型在流场短时预测效果上的优劣。

2. 引入非线性方程的神经网络

2.1. 神经网络模型

从结构上讲，神经网络模型包括全连接神经网络(FCNN)，卷积神经网络(CNN)，递归神经网络(RNN)以及各种神经网络模型的变体。不同结构的神经网络都有其适合处理的问题，比如：FCNN具有很好的普适性，CNN对图像问题有很好的表现，RNN对时间序列数据具有较高的精度。从神经网络的层数上来说，神经网络模型可以分为浅层神经网络和深度神经网络模型，二者的区分没有明确的界限，一般将小于等于3层的归为浅层，更多层数的都可以归为深度神经网络模型，理论上来说相同条件下深度神经网络比浅层神经网络具有更好的拟合效果 [16]。

神经网络主要包括四个要素：神经元，激活函数，损失函数，误差反向传播算法：神经元是神经网络的基本单位；激活函数是神经网络的非线性因素，使神经网络具有非线性拟合能力；损失函数描述了模型预测值与真实值之间的误差；误差反向传播算法是使用梯度下降法以及链式求导法则最小化损失函数并更新模型参数的方法。

神经元将上一层神经元的输出作为其输入，并经过激活函数的非线性作用得到自身的输出，其数学形式如下：

$x_{out}=f\left({\displaystyle \underset{i=1}{\overset{N}{\sum }}{w}_i{x}_i+b_i}\right)$ (1-1)

其中x_i表示上一层第i神经元的输出，也即第i个输入，w_i表示和上一层第i个神经元之间的连接权值，b_i为偏置，函数f表示非线性激活函数。

神经网络模型的输入通过内部神经元的层层传播，最终得到神经网络模型的输出y_out 。由于流场预测属于回归问题，则可以构建均方差损失函数(MSE)：

$loss=\frac{1}{2N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(y_i-y_{out}\right)}^2}$ (1-2)

最后使用误差反向传播算法可以进行loss的最小化，从而实现神经网络参数w_i，b_i的更新：

$\left(w_i,b_i\right)=\arg \underset{w_i,b_i}{\min }loss$ (1-3)

2.2. 引入非线性方程的神经网络模型

考虑非线性偏微分方程：

$\Omega \left(\left(x_1,x_2,\cdots ,x_i,\cdots ,x_{n-1},x_n\right);\lambda \right)=0$ (1-4)

式中x_i表示与偏微分方程相关的物理量，即方程的参数，λ表示偏微分方程的系数。

定义辅助函数h：

$h=\Omega \left(\left(x_1,x_2,\cdots ,x_i,\cdots ,x_{n-1},x_n\right);\lambda \right)$ (1-5)

使用一部分参数作为神经网络的输入值，另一部分作为输出值，则根据模型输入值以及输出值，可以对h进行计算，若使得 $\Vert h\Vert$ 的值逼近于0，则表明神经网络的输出值无限接近于满足对应的非线性偏微分方程。所以为了对神经网络模型耦合偏微分方程，不仅需要对损失函数loss最小化，同时还要对 $\Vert h\Vert$ 进行最小化。因此最终的损失函数可以由两部分构成：

$los{s}_{total}=loss+\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\Vert h\Vert }^2}=\frac{1}{2N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(y_i-y_{out}\right)}^2}+\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\Vert h\Vert }^2}$ (1-6)

那么，使用误差反向传播算法对神经网络参数的更新：

$\left(w_i,b_i\right)=\arg \underset{w_i,b_i}{\min }los{s}_{total}$ (1-7)

使用这样的方法，无论非线性偏微分方程多么繁杂，都可以简单明了地将其嵌入到神经网络模型中去。同时在损失函数中引入关于非线性偏微分方程的损失项，相当于机器学习理论中对损失函数添加的正则化项，可以有效地防止过拟合。

确定模型的算法流程如图1所示：

Figure 1. Algorithm flow

图1. 算法流程

本文采用6个隐藏层的全连接深度神经网络作为问题的研究工具，每个隐藏层包含50个神经网络节点，使用tanh激活函数，Adam优化算法，初始学习率设置为0.005。

3. 控制方程的耦合以及流场预测

3.1. 案例及数据概况

本文所研究的实例为不可压缩流体的二维圆柱扰流 [13] [14] 问题，雷诺数为100，这种情况下可以表现出稳定的层流卡门涡街现象。如图2所示，所选择的数据来自层流二维圆柱扰流尾流场高精度解(基于Nektar++的谱/hp有限元法得到 [17] )。本文的工作都基于数据采集区展开。

其中：

时间 $t\in \left[0,\text{2}\right]$， $N_t\in \left[0,\text{199}\right]$，共计200个时刻；

Figure 2. Data collection

图2. 数据采集

横坐标 $x\in \left[\text{1},\text{8}\right]$， $N_x\in \left[0,\text{99}\right]$，均分为100个横坐标。

纵坐标 $y\in \left[-\text{2},\text{2}\right]$， $N_y\in \left[0,\text{49}\right]$，均分为50个纵坐标。

每个时刻包含5000个坐标点，总数据量为100万个，所包含的状态量有：x方向速度u，y方向速度v，以及压力p。以[x, y, t]作为神经网络模型的输入值，以[u, v, p]作为神经网络模型的输出值。

3.2. 控制方程的耦合

在计算流体力学中，就本例而言，所需要的控制方程包括连续性方程以及动量守恒方程(N-S方程，忽略质量力)：

连续性方程：

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$ (2-1)

N-S方程：

$\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{\partial p}{\partial x}+0.01\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)$ (2-2)

$\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{\partial p}{\partial y}+0.01\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)$ (2-3)

根据1.2中在神经网络模型中引入非线性偏微分方程的方法，定义h_c，h_u，h_v如下：

$h_c=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}$ (2-4)

$h_u=\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\frac{\partial p}{\partial x}-0.01\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)$ (2-5)

$h_v=\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\frac{\partial p}{\partial y}-0.01\left(\frac{{\partial }^{2}v}{\partial x^2}+\frac{{\partial }^{2}v}{\partial y^2}\right)$ (2-6)

本例中，没有耦合控制方程(纯数据驱动模型)的损失函数为：

$loss=\frac{1}{2N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(u_i^t-u_i^p\right)}^2}+\frac{1}{2N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(v_i^t-v_i^p\right)}^2}+\frac{1}{2N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left(p_i^t-p_i^p\right)}^2}$ (2-7)

式中： $u_i^t$， $v_i^t$， $p_i^t$ 为速度压力的真实值， $u_i^p$， $v_i^p$， $p_i^p$ 为神经网络给出的速度压力的预测值。

通过神经网络的预测值以及神经网络的输入值可以对h_c，h_u，h_v进行计算，并对其最小化，使得神经网络模型的输出值满足连续性方程和N-S方程，实现对流体动力学方程的近似求解。若将其看成损失函数的一部分，那么最终的损失函数可以写为：

$los{s}_{total}=loss+los{s}_{h_c}+los{s}_{h_u}+los{s}_{h_v}$ (2-8)

其中：

$los{s}_{h_c}=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\Vert h_c\Vert }^2}$ (2-9)

$los{s}_{h_u}=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\Vert h_u\Vert }^2}$ (2-10)

$los{s}_{h_v}=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\Vert h_v\Vert }^2}$ (2-11)

通过这种方式，可以成功将流体力学问题的控制方程嵌入到神经网络模型中。

3.3. N-S方程近似求解

使用N_t = 0到N_t = 99内50万个数据，从中随机选取5000个点进行模型的训练，训练步数30,000步。使用训练完成的神经网络模型，对0~99 N_t的数据采集区的速度场和压力场进行重建。选择N_t = 50时刻的压力场和速度场计算结果，结果如下：

定义L2范数相对误差：

$\text{L2\_error}=\frac{{\Vert U_{true}-U_{pred}\Vert }_2}{{\Vert U_{true}\Vert }_2}$ (2-12)

式中U_true，U_pred分别表示流场状态量的真实值以及神经网络预测值的向量形式。

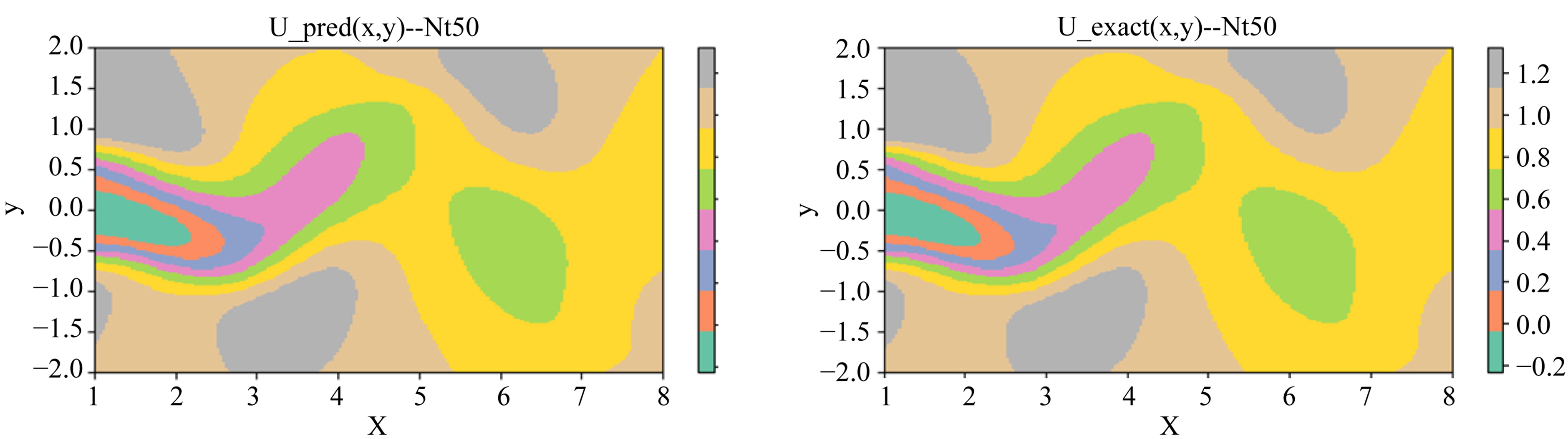
Figure 3. N_t = 50 Predicted velocity field and real velocity field of x-direction

图3. N_t = 50时刻x方向预测速度场与真实速度场

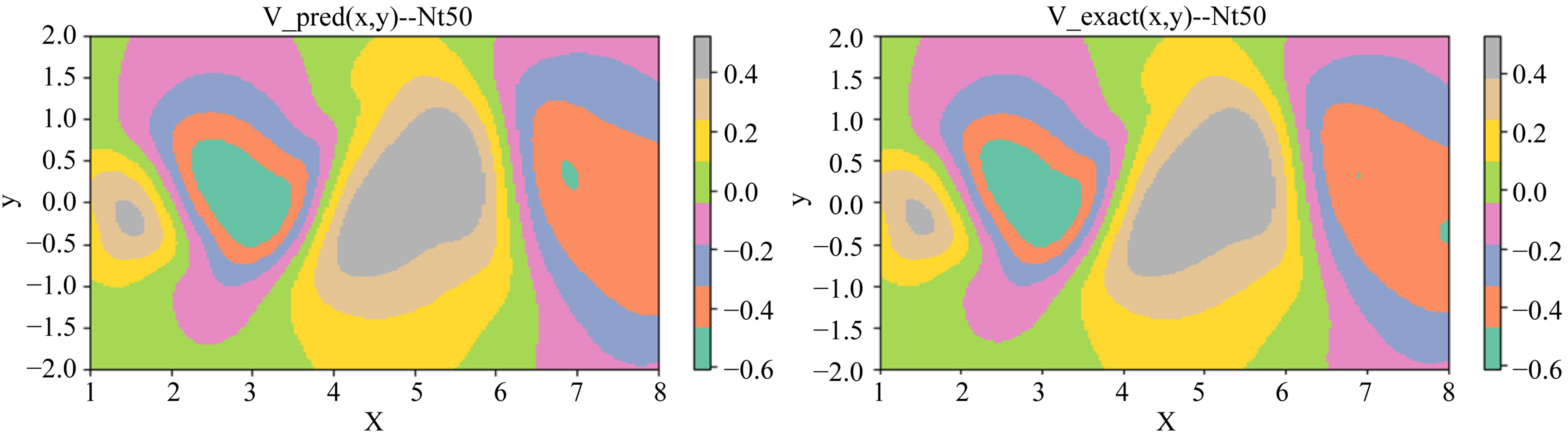
Figure 4. N_t = 50 Predicted velocity field and real velocity field of y-direction

图4. N_t = 50时刻y方向预测速度场与真实速度场

Figure 5. N_t = 50 Predicted and actual pressure fields

图5. N_t = 50时刻预测压力场与真实压力场

对 $N_t=\left\{10,20,30,40,50,60,70,80,90\right\}$ 的速度和压力的L2范数相对误差进行计算，结果如下：

Table 1. The L2 norm relative error between the true value and the predicted value of u, v, p at the main moment

表1. 主要时刻u, v, p的真实值与预测值的L2范数相对误差

通过图3~5可以直观地看出该神经网络模型重建的速度场和压力场可以与真实流场良好的吻合。由表1可知，神经网络模型在各个时刻重建的流场具有很小的L2范数相对误差，表明模型可以实现对计算域内流场的准确建模，实现了对控制方程组的近似求解。

3.4. 基于神经网络流场预测模型

流场的预测在气象，风电等领域都有实际应用需求，但是实际过程往往存在建模困难等实际问题，所以考虑使用神经网络模型作为短期的流场预测模型。依旧采用二维圆柱扰流的数据集，以x方向速度u的流场短时预测效果为研究对象，L2范数相对误差为评价指标，对耦合控制方程的神经网络流场预测模型和纯数据驱动的神经网络流场预测模型进行对比验证。

由于涉及到未知时刻的流场预测，需要充分利用现有数据，故可以在计算能力之内，适当增加训练时用的数据量。使用N_t = 0到N_t = 99内50万个数据，从50万数据点中随机选取50,000个数据(保证每个时刻5000个点中选择500个数据点)作为训练数据，训练步数为30,000步，而验证数据集选择完全未知的100~120 N_t时刻的数据，进行两种方法对流场未来趋势预测能力对比验证。使用训练完成的两个神经网络模型，以速度u为例，分别对N_t = 110的x方向速度u进行预测结果如下：

从图6，图7中可以直观的看出：除去一些细微的差别，两种神经网络流场预测模型都可以实现对N_t = 110时刻的尾流场的预测，预测结果与真实流场基本吻合。

为了从L2范数相对误差上进一步说明二者的预测能力的差别，对两种神经网络模型进行五次试验，二者使用相同的训练数据集，但每次使用的训练数据集不同，训练步数均为30,000步，其他超参数保持不变。每次使用训练好的模型分别对N_t = {100, 102, 104, 106, 108, 110, 112, 114, 116, 118, 120}时刻的x方向速度u进行预测，并计算五次各个时刻的平均L2范数相对误差，结果如下：

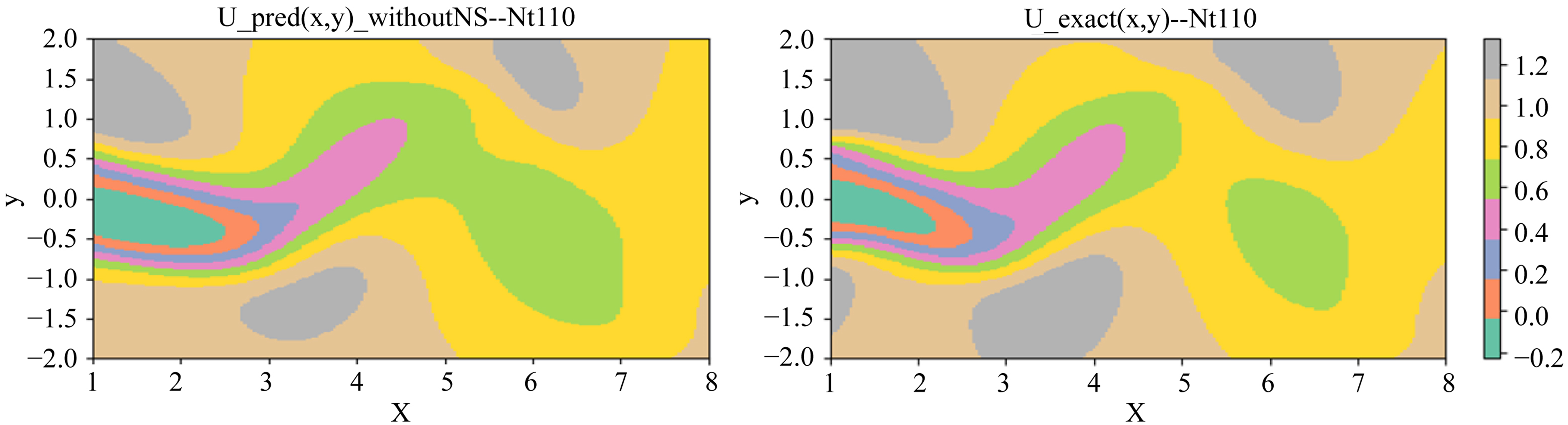
Figure 6. N_t = 110 The predicted results of pure data-driven neural network model

图6. N_t = 110纯数据驱动神经网络模型预测结果

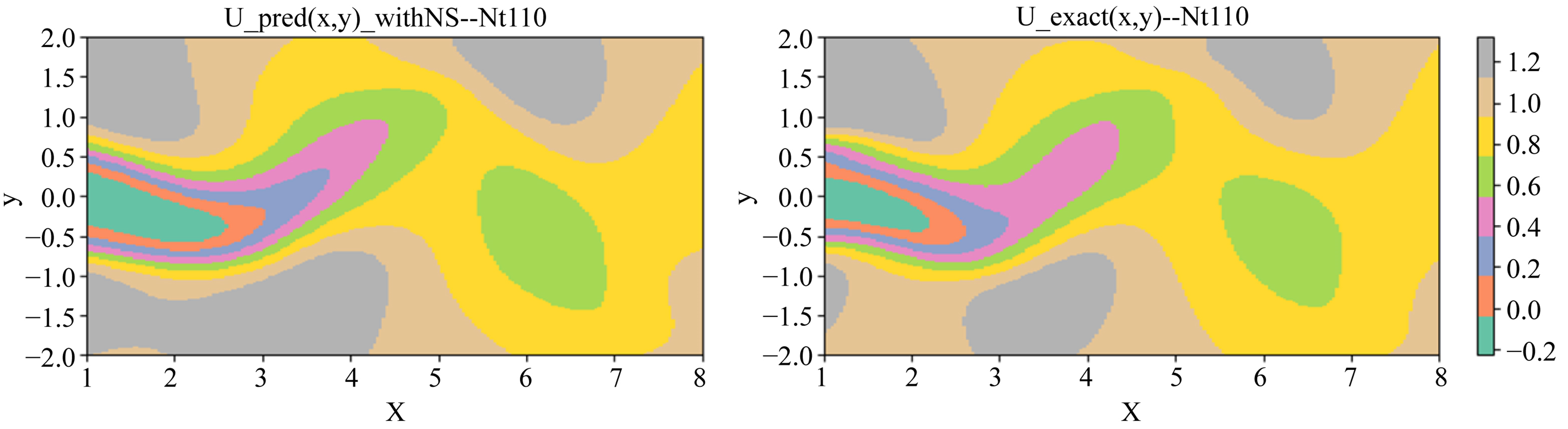
Figure 7. N_t = 110 The predicted results neural network model coupled with governing equations

图7. N_t = 110耦合控制方程的神经网络模型预测结果

从图8中可以看出，作为流场的短时预测模型，二者都实现了不错的预测效果，但是与纯数据驱动的神经网络流场预测模型相比，耦合控制方程的模型在短时流场预测中具有更小L2范数相对误差，而且具有更小的误差增长速率。这表明在神经网络模型中耦合控制方程，增加物理定律的约束，可以一定程度上提高模型的预测能力。

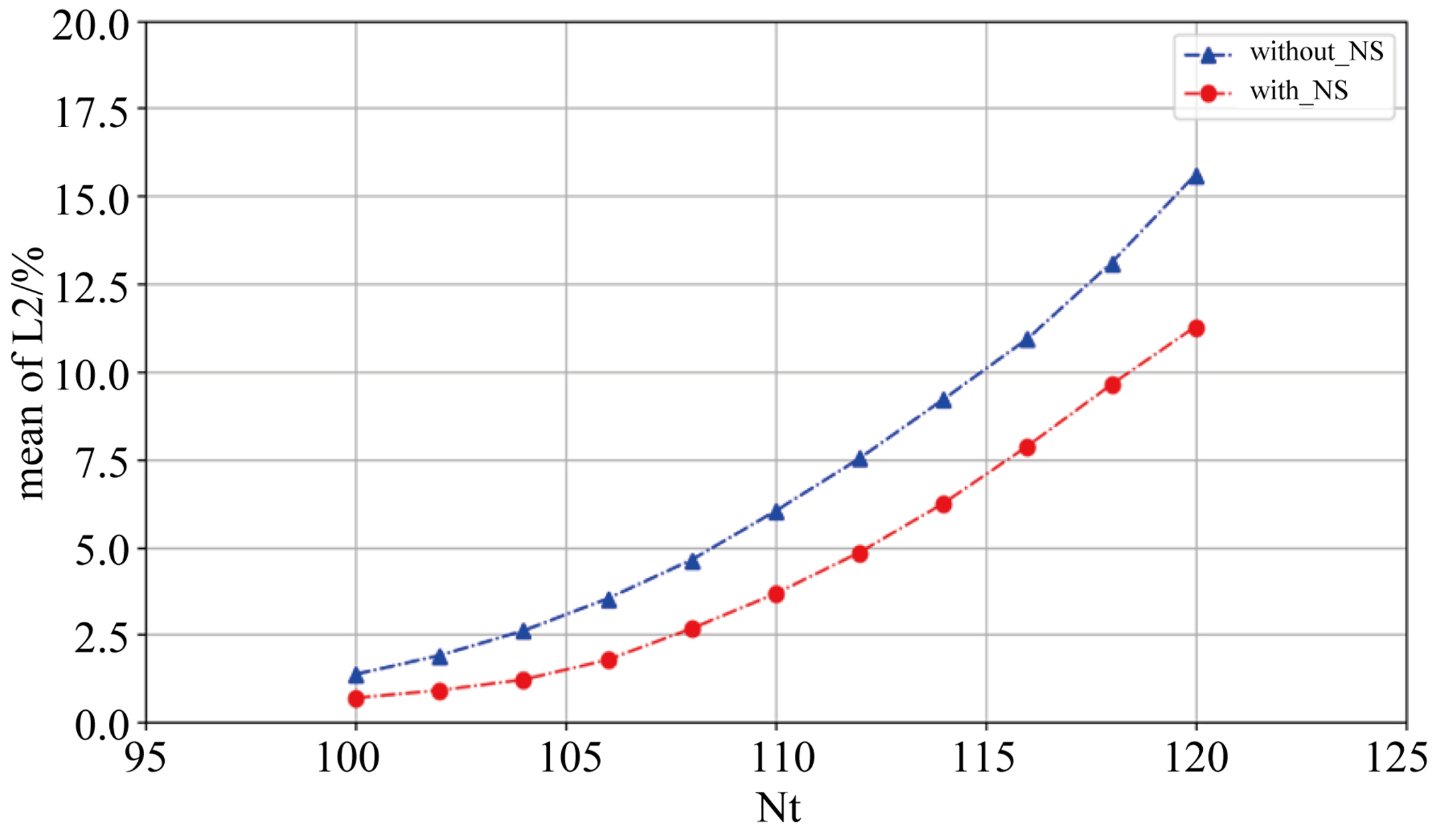
Figure 8. The average L2 norm relative error of two models

图8. 两种模型平均L2范数相对误差

4. 结论

(1) 以层流二维圆柱扰流为例，提出了耦合控制方程(组)的一般方法，开发了耦合流体动力学方程的神经网络模型，并利用少量数据实现了对相应区域流场的重建以及控制方程的近似求解。

(2) 以流场的短时预测为研究对象，对比了纯数据驱动与耦合控制方程的神经网络流场预测模型的流场预测能力，表明相同条件下后者具有更高的预测精度。

(3) 虽然这种方法取得了不错的效果，但是由于神经网络模型嵌入了过多的非线性方程，导致引入了更多的矩阵运算，所以模型的训练代价较大，所以在未来的工作中，会将重点放在模型的优化上，同时考虑应用在更加复杂的流动问题上。

参考文献

NOTES

^*通讯作者。