1. 引言
时空复杂网络模型是一种既依赖于时间又依赖于空间的复杂网络模型,该模型可以精确描述自然界中许多复杂的扩散现象,例如化学反应中物质浓度的变化 [1],入侵物种在生态种群中的扩张现象 [2]。此外,空间扩散也经常发生在复杂系统中。一个典型的例子是:神经网络中的电子在非均匀电磁场中运动时,空间扩散是不可避免的。同步现象在我们日常生活中普遍存在,比如钟摆的同步摆动,一群萤火虫同步发光等等。在20世纪90年代初,这一概念被Pecora和Carrol引入到混沌系统中 [3]。在接下来的几十年里,复杂网络的同步控制由于其在生物工程 [4]、加密通信 [5] 等方面的成功应用引起了来自不同学科领域的广泛关注。鉴于这些事实,考虑时空复杂网络的同步是合理且具有现实意义的。
边界控制是时空复杂网络同步控制中一种经典的控制手段,它只对位于空间边界上的节点施加控制而不是整个空间域上的所有节点,这在空间维度上有效地节省了控制成本。近年来,基于边界控制的时空复杂网络同步问题的研究已取得了初步进展。例如,学者们利用反推方法,通过边界控制研究了一类满足Dirichlet边界条件的耦合时空系统的同步问题 [6]。而在文献 [7] 和 [8] 中,利用Lyapunov方法,讨论了边界控制下一类满足Neumann边界条件的耦合时空网络的同步问题。特别地,在文献 [7] 中,设计了线性状态反馈边界控制器,与之不同的是文献 [8] 设计了带有边界测量的状态反馈控制器。注意到这些理论工作中不可避免地运用到了变量变换方法,并依此建立起了基于高维线性矩阵不等式的同步判据,这在实践中是难以实施和验证的。此外,上述研究工作中的模型只涉及状态耦合。而在现实世界中,由于个体的不同扩散可能会导致其他个体的不同变化,例如,入侵物种的存在可能导致捕食–猎物系统中某一物种的种群流动,这种现象可以通过带有空间扩散耦合的时空网络来描述。目前,基于边界控制研究具有空间扩散耦合的时空网络同步仍然是一个开放性的课题,且在分析过程中避免变量变换从而建立简单易于验证的同步判据也是一项具有挑战性的工作。
需要注意的是,上述结果主要集中研究时空网络的渐近或指数同步问题,即只有当时间接近无穷大时才能实现同步,这在实际工程应用中是不合理,特别是对于寿命有限的生物和设备来说并不现实。为了加快网络的收敛速度,文献 [9] 中提出了有限时间同步的概念。近年来,由于有限时间同步在抗干扰 [10] 和鲁棒性 [11] 方面表现出良好的性能,因此众多学者将目光由时空网络的渐近同步转向有限时间同步。文献 [12] 中设计了包含线性反馈项和非线性反馈项的边界控制器,并通过构造Lyapunov函数,分析并证明了在所设计的控制器下,网络可以实现有限时间同步。在 [13] 中研究了边界控制下反应扩散系统的有限时间镇定问题。特别值得注意的是,他们的工作中反应扩散系统满足由Dirichlet边界条件和Neumann边界条件组成的混合边界条件,这一前提条件大大降低了理论分析的复杂性。遗憾的是,上述条件在时空网络的边界同步控制工作中很少涉及。还注意到,上述同步结果中的停息时间严重依赖于目标系统的初始状态,而提前访问目标系统的初始状态是非常困难的。因此,Polyakov在 [14] 中提出了固定时间稳定的概念,其收敛时间不依赖于初始状态的信息。目前,关于固定时间的理论成果已经逐渐成熟如 [15] 和 [16] 中的工作,并广泛应用到不同时空网络模型的固定时间同步控制研究中,如一类带有时变时滞的不连续反应扩散网络 [17],复值忆阻反应扩散神经网络 [18]。而在文献 [19] 中,基于反推方法,设计了边界时变反馈控制器来解决了带有不变参数的反应扩散系统的固定时间镇定问题。然而,在Lyapunov方法下,时空复杂网络的固定时间边界同步问题的研究仍然是一个开放且噬待解决的课题。
基于上述分析,本文将基于边界控制探讨具有混合耦合的时空复杂网络固定时间同步问题。主要结果包含如下几个方面。第一,建立了具有状态耦合和空间扩散耦合的时空复杂网络模型,该模型比 [12] [13] [17] [18] [19] 中的模型更符合现实世界。第二,设计了不包含线性反馈项的固定时间边界控制策略,它同样适用于 [12] 和 [13] 中的结果,与之不同的是本文设计的控制器相对简单且估计的停息时间不依赖于初始状态的信息。第三,通过对同步误差构造Lyapunov函数,建立了相比 [7] [8] [12] 中形式简单的固定时间充分判据。此外,理论分析过程中避免了 [7] [8] [12] 中采用的变量变换,降低了理论推导难度。
符号说明:
是n维数实向量空间;
是
维实矩阵空间;对任意的向量
,二范数定义为:
,其中
代表向量y的转置;对任意的矩阵P,
和
分别代表矩阵P的最小特征值和最大特征值;且矩阵范数定义为:
;
代表P的逆;
为
维单位阵;
代表元素全为0的列向量;
;
表示矩阵P正定;
表示对角阵;
Kronecker积。
2. 预备知识
2.1. 模型描述
考虑如下具有空间扩散耦合和状态耦合的时空网络模型:
(1)
其中
;
是第r个节点的时空状态;
代表拉普拉斯算子;
是一个连续的非线性向量函数;
是
上连续且有界的初值解;
代表传播扩散矩阵;A和B是
维实矩阵;
代表整体耦合强度;
和
是正定的内耦合矩阵;
表示网络的拓扑结构,其中如果节点r和节点j之间存在通信,那么
,否则
,此外
。
系统(1)满足如下混合边界条件:
(2)
其中
是控制器。
设孤立节点的状态为系统(1)的同步态,且满足下列动力学方程:
(3)
定义
,则同步误差系统为:
(4)
其中
。
定义1. [15] 对系统(1)和(3)满足不同初始条件和边界条件的任意解
和
,若存在固定的时间
和停息函数
使得
且
,则称系统(1)是固定时间同步的。
2.2. 引理和假设
为了得到主要结果,下面引入一些必要的假设和引理。
引理1. [13] 假设
是连续且平方可积的函数,满足
或
,则对于
有
引理2. [15] 如果存在一个正则,正定且径向无界的函数
使得:
其中
,
,
,
,则以下结果成立:
(1) 若
,则当
时有
,
,且
满足:
其中
。
(2) 若
,则当
时有
,
,且
满足:
其中Beta函数比率
定义为
且Beta函数
定义为
其中
,
,
。
(1) 若
,
,则当
时有
,
,且
满足:
引理3. [16] 设
,
,
。则有
假设1. 对于任意向量
,存在常数
使得
3. 主要结果及证明
为实现系统(1)的固定时间同步,设计如下边界控制策略:
(5)
其中,
,
,
,
是对称矩阵且
为了方便后续分析,记
利用Kronecker积,将系统(5)改写为:
(6)
其中
,
,
。
定理1 基于假设1及边界控制器(5),如果存在矩阵
,使得
则下列结果成立:
(1) 当
时,受控网络(1)是固定时间同步的,且停息时间
满足
其中
,
,
,
,且M满足
。
(2) 当
时,受控网络(1)在固定时间
内实现同步,且
满足
(3) 当
,
时,受控网络(1)是固定时间同步的,且停息时间
满足
证明:构造如下Lyapunov函数
对任意
,
沿着系统(6)关于变量t求导可得
(7)
根据假设1,我们有
(8)
利用分部积分和系统(1)中的混合边界条件,可以推得
(9)
类似可得
(10)
根据混合边界条件(2)以及引理1,当
时,结合(9)和(10)可得到下列不等式
(11)
由边界控制方案(5)可知
(12)
和
(13)
其中
由(12)和(13),
(14)
其次,考虑引理3以及
,
,我们有
将它们带入(14)得
(15)
最后,将(8)~(15)带入(7)式,则对所有的
有
此外,根据矩阵分解理论,必存在一个实可逆矩阵M使得
,则有下列不等式成立:
因此,我们有
若对所有的
有
,即满足引理2中的情况(1),则系统(1)在
内达到同步。
若对所有的
有
,即满足引理2中的情况(2),则系统(1)在
内达到同步。
若
,
,根据引理2中的情况(2),则系统(1)在
内达到同步。
证毕。
4. 数值模拟
考虑如下三维时空复杂系统:
(16)
和具有100个节点的耦合时空复杂系统:
(17)
其中
,
,其他参数选为:
,
,
,
,
且
网络(17)的拓扑结构如图1。图2~4模拟了系统(16)的动态演化过程,其中初始值为:
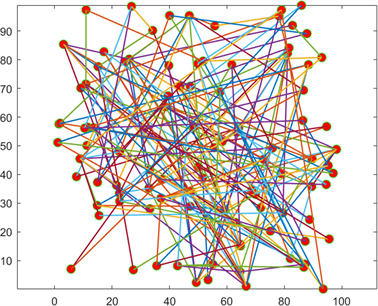
Figure 1. Curve: Topology structure of the network (17)
图1. 网络(17)的拓扑结构

Figure 2. Curve: The dynamical behavior of
图2.
的动态行为
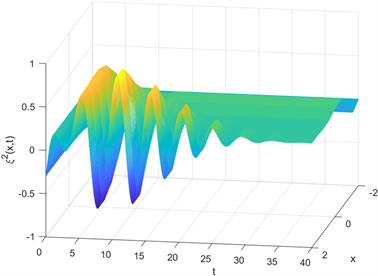
Figure 3. Curve: The dynamical behavior of
图3.
的动态行为

Figure 4. Curve: The dynamical behavior of
图4.
的动态行为
接下来,在边界控制方案(5)下,验证系统(17)的在固定时间内达到同步。很容易验证当
时,
。通过简单计算可知
,
。选择控制器参数
,
,
,由定理1,系统(17)在
内达到固定时间同步。模拟结果见图5~8。

Figure 5. Curve: Synchronization error
图5. 同步误差
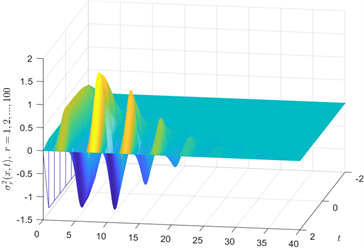
Figure 6. Curve: Synchronization error
图6. 同步误差
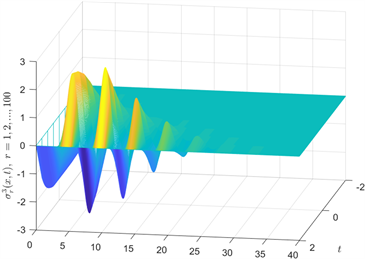
Figure 7. Curve: Synchronization error
图7. 同步误差
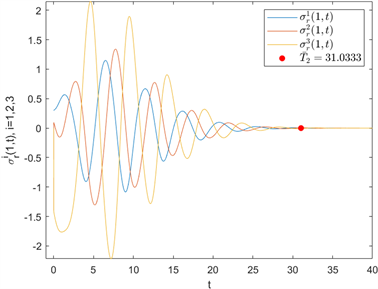
Figure 8. Curve: Fixed-time synchronization error of (17)
图8. 系统(17)的固定时间同步误差
5. 结论
本文研究了带有空间扩散耦合的时空复杂网络的固定同步问题。首先,设计了高效的且不包含线性反馈项的固定时间边界控制器。然后通过构造Lyapunov函数,结合分部积分、线性矩阵不等式技巧,建立了形式简单且易于验证的固定时间同步判据。此外,在理论分析过程中,避免了文献 [7] [8] [12] 中使用的变量变换法,降低了理论推导的难度。本文的方法可以拓展到边界控制下仅带有状态耦合的时空复杂网络固定时间同步研究中,还可以进一步研究时空复杂网络的指定时间边界同步问题。