1. 引言
量子隧穿作为没有经典对应的纯粹量子力学现象,是指微观粒子能量低于势垒高度时穿越势垒的行为。利用量子隧穿效应能够解释星际云中氢键的形成和恒星核聚变 [1] 以及放射性衰变 [2]。但量子隧穿中可能存在的超光速现象令人困惑,所以量子隧穿时间作为衡量隧穿过程一个关键的动力学量——其存在的问题仍然亟待澄清。量子隧穿时间最早起源于Condon [3] 提出的量子隧穿相速度问题。1932年MacColl [4] 首次完成含时薛定谔方程的近似波包分析,给出隧穿时间的表达式,并认为隧穿几乎不需要明显的时间就能发生。此后量子隧穿时间一直是该领域争论的焦点 [5]。正如泡利 [6] 所说,不同于诸如动量在内的其他力学量算符,理论上似乎无法得到一个与Hamiltonian共轭的时间算符,时间在量子力学中只是一个参量。由于物理学大家的否定性断言,对量子隧穿中时间问题的讨论沉寂了几十年。直到1962年,Hartman [7] 发现相比于自由区域,势垒似乎为粒子提供了“捷径”,粒子通过势垒所花的时间似乎更少,且Hartman在文章中得到一个令人惊讶的结论:宽势垒的隧穿时间与势垒宽度无关 [7]。这一结论意味着如果势垒足够宽,就会出现超光速现象。该结论似乎和Einstein的相对论因果关系相冲突,因而引起了巨大的争论。之后,人们为了得到一个能够很好度量隧穿时间的物理量,产生了很多不同的隧穿时间定义 [8] [9] [10]。迄今为止,定义隧穿时间的方法一般分为以下几类——第一类是跟踪波包的特征(如波峰)运动来定义时间。第二类是对粒子可能的经典路径取Feynman平均,即对于一组可能的经典路径,求出粒子在势垒中每一条路径上花费的时间,然后再对这些时间求Feynman平均。第三类是引进新的自由度,构造与运动粒子耦合的物理时钟来测量量子隧穿时间。此外,还有一种非常重要的隧穿时间——即驻留时间,该时间定义比较清晰,因为它不区分粒子最终是透射离开势垒还是被势垒反射回去,它仅代表粒子与势垒作用的平均时间。诸多的时间定义各有优劣,目前尚无学界充分认可接受的标准时间定义,部分原因是缺少经典对应,部分原因则是缺少较为可信的实验。
近年来,随着超快激光技术的发展,实验上对隧穿时间的测量有了新的进展。2014年,Keller [11] 实验室利用“阿秒钟”技术(“阿秒钟”是指原子中的电子遇到一个原子实库伦势、激光线性势和原子实偶极势的叠加势垒,当发生隧穿附近自由电子的动量分布与激光电场诱导的隧穿方向间存在一个可定义为时间延迟的角度)测得氦原子隧穿时间为50阿秒。而Litvinyuk [12] 等人认为对于多电子原子,既无法准确建模,也令电离动力学的解释更为复杂化。因此Litvinyuk等人为了解决这一问题在2019年用更为简单的氢原子进行实验,测得氢原子的隧穿时间为1.8阿秒。但“阿秒钟”实验存在一个问题:电子并不是直接撞击势垒,而是从准束缚态中逃逸出来的,所以隧穿的“开始”时间存在争议 [13]。2019年7月,Steinberg [13] 等人使用“拉莫尔钟”对量子隧穿时间进行了测量,利用玻色爱因斯坦凝聚态下的铷原子穿过具有伪磁场的势垒,通过原子的赝自旋进动测得隧穿时间大约为0.62毫秒。就目前已知的定义来看,“拉莫尔钟”给出隧穿时间的测量结果比较令人信服,也是我们后期研究的重点。本文中,第二部分我们简要回顾了薛定谔方程的解,并得到在三角势垒定态波函数的精确解;第三部分,我们计算了微观粒子穿过三角势垒的透射相位时间和反射相位时间,并作出相位时间随波数k的变化情况;在第四部分,我们计算了通过三角势垒的驻留时间,并通过图像显示了驻留时间与波数k的关系,最后我们对三角势垒的隧穿时间进行了分析与总结。
2. 三角势垒下薛定谔方程的解
在讨论量子隧穿时间之前,我们先简单回顾一下能量为
的中子在右直角三角势垒(如图1所示)中运动的量子描述。我们令三角势垒左侧斜率为
,右侧斜率无穷大,则有:
(1)
其中l为势垒的宽度,且
为三角势垒的高度。

Figure 1. Particles pass through a triangular barrier
图1. 粒子通过三角势垒的隧穿
考虑一般的含时薛定谔方程:
(2)
对(2)式进行分离变量,则有特解
。其中
是波包
的傅里叶
展开的权重因子,而
是本征能量为 的定态波函数,可以通过求解定态薛定谔方程得到:
(3)
作为初步,同时也为计算简便,我们仅探讨定态薛定谔方程的解并给出在单色近似
下的隧穿时间,这相当于求解非局域的平面波解。更为一般化的含时薛定谔方程的波包解我们留待以后研究。
将(1)式中三角势垒的具体形式带入到(3)式中,其中我们定义特征长度
,从而可得特征能量
,假定三个不同区域波函数的解:
(4)
(5)
(6)
其中
,
;R和T为反射和透射振幅。利用波函数在
和
处的连续性条件:
(7)
(8)
(9)
(10)
其中
,可以分别求出四个系数:
(11)
(7)~(10)式中的M、P、Q、J、F分别为:
(12)
确定四个系数后,自然确定了波函数的精确解。波函数模方随 的变化如图2所示,其中我们选取中子质量和6 μm−1的波数k,绿色、蓝色和粉色的实线分别为势垒宽度一致(均为4 nm)时,在三种不同势垒高度下
随z的变化情况。通过图2可以看出:在势垒宽度一致时,当势垒高度越高时波函数的模方
也越大,表现为粒子在势垒中出现的几率密度随势垒高度增加而增大。
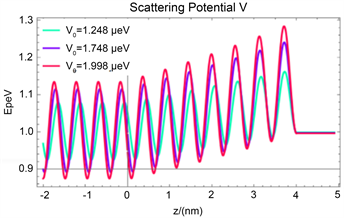
Figure 2. Wave function modulo as a function of z
图2. 波函数模方随 的变化情况
3. 三角势垒的相位时间
在我们计算三角势垒的相位时间之前,先简要回顾下相位时间,或称为Eisenbud-Wigner [8] 时间,它是通过跟踪入射波包的相位变化来定义的。考虑一个能量集中在
的分布很窄的入射波包
向一个宽度为l的势垒运动,撞上势垒后透射波包和反射波包分别为:
(13)
(14)
对于透射波包,跟随波峰
的运动,在稳态相位近似 [14] 下满足方程:
(15)
显然,隧穿引起了空间延迟
和透射时间延迟:
(16)
其中
是群速度。同理,我们可以得到反射相位时间延迟为:
(17)
假定在k-空间的窄波包近似下,根据(16)和(17)式对于相位时间延迟的定义,可以计算出三角势垒下的透射相位时间延迟(某种程度上等价于计算Peres时间 [15] ):
(18)
为了令反射相位时间的表达式更为紧凑,我们作如下定义:
,
(19)
,
,
其中
,则反射相位时间为:
(20)
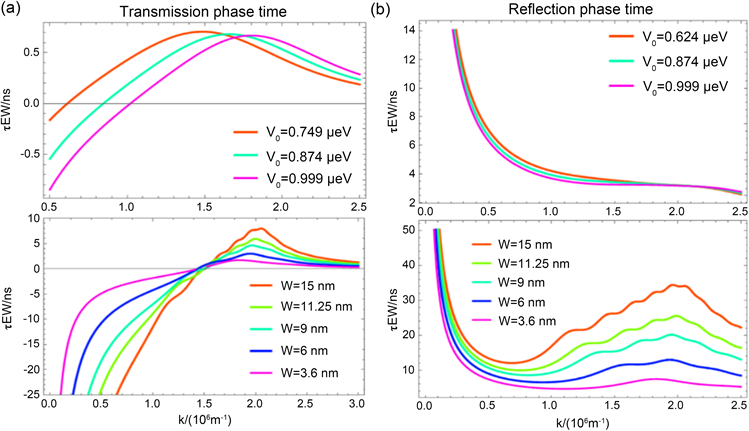 注:(a)图中的顶部是粒子在势垒宽度均为2 nm相同时,不同势垒高度下的透射相位时间;(a)图底部为势垒高度(1.13 μev)一致时,不同势垒宽度下的透射相位时间。(b)图中顶部是粒子在势垒宽度相同均为2 nm时,不同势垒高度下的反射相位时间;(b)图底部为势垒高度(1.13 μev)一致时,不同势垒宽度下的反射相位时间。
注:(a)图中的顶部是粒子在势垒宽度均为2 nm相同时,不同势垒高度下的透射相位时间;(a)图底部为势垒高度(1.13 μev)一致时,不同势垒宽度下的透射相位时间。(b)图中顶部是粒子在势垒宽度相同均为2 nm时,不同势垒高度下的反射相位时间;(b)图底部为势垒高度(1.13 μev)一致时,不同势垒宽度下的反射相位时间。
Figure 3. Phase time as a function of wave number k
图3. 相位时间随波数k的变化
图3是相位时间随波数 的变化情况,其中(a)图为透射相位时间随波数k的变化,(b)图是反射相位时间与波数k的关系。(a)图顶部显示了透射相位时间在三角势垒宽度为
,粒子质量为中子质量,
势垒斜率
,特征能量为
时,三种不同势垒高度下透射相位时间与波数k的关系。
在势垒宽度相同时,随着波数k的增大,三种不同高度下的透射相位时间均随着波数k的增加先增加后减小,出现峰值;其峰值的变化如表1所示:

Table 1. Transmission time peaks and corresponding k values at different heights with the same barrier widths
表1. 势垒宽度相同时,不同高度下的透射时间峰值及对应的k值
由表1可以明显看出势垒宽度一致时,随着势垒高度增加,意味着三角势垒的斜率增大(势垒陡峭),透射时间峰值逐渐下降;其峰值对应的k值增加(峰右移)。
图3(a)底部为三角势垒高度(1.8 μeV)不变时,五种不同势垒宽度下的透射相位时间。通过图3(a)底部可以看出:在势垒宽度取五个不同值时,随着波数k的增大,透射相位时间都是先增加后减小,出现峰值;其峰值的变化如表2所示:

Table 2. Transmission time peaks and corresponding k values at different width with the same barrier height
表2. 势垒高度相同时,不同宽度下的透射时间峰值及对应的k值
通过表2可以明显看出:当势垒宽度增加,且势垒高度不变,即三角势垒的斜率减小(势垒平缓),透射相位时间峰值变大,且随着势垒宽度的增加,时间峰值对应的k值变大,出现峰右移;同时透射相位时间出现振荡,与势垒宽度较小时对比,如势垒宽度为15 nm和势垒宽度为3.6 nm,势垒越宽振荡越明显,原因之一可能是:势垒越宽,意味着势垒越平缓,对应的入射、反射分波具有更大的干涉重叠区,因而干涉越明显,所以表现为振荡越明显。
对比图3(a)顶部和底部可以发现:无论势垒高度相同或势垒宽度相同,粒子的透射相位时间均随波数k的增大先增加后减小——即出现峰值;且随势垒宽度增加或势垒高度的减小,相位时间峰值所对应的k值都会变大,峰右移;将峰作为特征时间似乎并不奇怪,粒子能量越高,隧穿深度越深,自然越陡峭的势垒也越难隧穿,故而对于隧穿时间的峰值对应的k也越大,但隧穿的相位时间反而越小;而对同一高度不同宽度的势垒,峰值k越大,其对应隧穿深度越大,相应相位时间自然也越大;且相位时间明显的振荡行为出现在宽度较大时,而窄势垒下单纯高度的变化并不会有振荡行为产生。
图3(b)顶部为反射相位时间在三种不同势垒高度下,势垒宽度为2 nm时的变化情况。其中随着波数k的增加,反射相位时间逐渐减小;即使改变势垒高度,反射相位时间随波数k的变化趋势几乎一致,无明显的峰出现,这是符合我们预期的:k越大,速度越快,势垒宽度不变自然反射时间越短;而势垒高度越高,势垒越硬,自然反射时间也越短;而当势垒高度相同(
),势垒宽度不同时,如图3(b)底部所示:反射相位时间出现明显区分。
图3(b)底部中反射相位时间在势垒宽度增大时,随着波数k的增加先减小后增大,即反射相位时间出现峰值。其原因是:当势垒不是太硬的时候,即斜率较小时,越大的k隧穿深度越大,带来反射时间的增加;另一方面,越大的k速度越快,又导致反射时间的减少;两者竞争的结果导致当k不是太大时,就会出现先增加后减少的趋势,因而出现峰值。且通过图(b),我们可以看出反射相位时间同透射相位时间一致,在高度一致,宽度增加时,峰值增加且峰右移;此外,反射相位时间在势垒宽度较大(15 nm)时有明显振荡,势垒宽度较小(3.6 nm)时,振荡不明显,而在2 nm时(图3(b)顶部)几乎没有振荡。
4. 三角势垒的驻留时间
除了相位时间,驻留时间也是隧穿时间较为重要的一种定义。作为对粒子在所有空间散射道(反射、透射)花费时间的平均度量,驻留时间
最早在1960年由Smith [9] 引进,1982年Büttiker [16] 给出了一维隧穿下驻留时间的表达式:
(21)
其中,
是势垒中的波函数,
是入射波的几率流。根据驻留时间的定义,结合(11)式中的四个系数解,
和
分别为积分的上下限,可以得到三角势垒的驻留时间为:
(22)
图4(a)中势垒高度不变时,驻留时间随着波数k的增加先增大后减小,出现峰值,通过表3可以明显看出:峰值对应的k值在0.097→0.200 μm−1的范围内,变化较小;势垒宽度增加,势垒高度不变时,势垒的斜率减小(势垒平缓),驻留时间的峰值变大,时间峰值对应的k值也增加,驻留时间峰右移;此外势垒宽度较宽时,驻留时间的振荡较为明显。
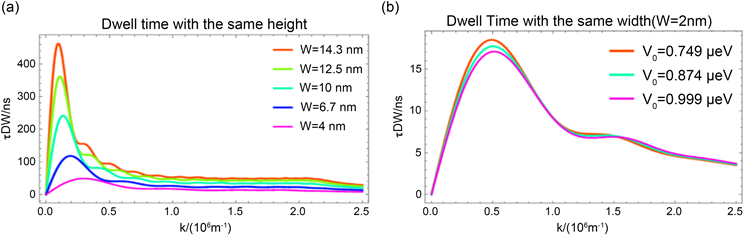 注:图(a)三角势垒高度一致时(为2 nm),不同宽度下的驻留时间,图(b)为三角势垒宽度一致时,不同高度下的驻留时间。
注:图(a)三角势垒高度一致时(为2 nm),不同宽度下的驻留时间,图(b)为三角势垒宽度一致时,不同高度下的驻留时间。
Figure 4. The dwell time as a function of wave number k
图4. 驻留时间随波数k的变化
图4(b)显示了:在势垒宽度不变时,当波数k增加时,驻留时间先增大后减小,出现峰值;表4中给出不同高度下的时间峰值和对应的k值,很显然随着势垒高度的增加,即势垒斜率变大(势垒陡峭),驻留时间的峰值变小,对应的k值变大,但变化较小,出现峰右移;k值较大时,驻留时间的变化趋势几乎一致。

Table 3. Dwell time peaks and corresponding k values at different width with the same barrier height
表3. 势垒高度相同时,不同宽度下的透射时间峰值及对应的k值

Table 4. Dwell time peaks and corresponding k values at different width with the same barrier height
表4. 势垒宽度相同时,不同高度下的透射时间峰值及对应的k值
驻留时间的变化同样合乎预期:同高度宽度增加,势垒变缓,对应的隧穿时间增加,表现为图4(a);等宽度势垒高度增加,势垒变陡峭,隧穿时间减少。
对比三角势垒相位时间和驻留时间可以发现:对于透射相位时间和反射相位时间随波数k的增加出现两种相反趋势的变化——即当势垒的宽度或高度不变时,透射相位时间随着波数k的增加先增大后减小,反射相位时间则是随着波数k的增加先减小后增大;但是对于相位时间和驻留时间有相同的变化——即随着波数k的变化过程中相位时间和驻留时间均先增加后减小,出现峰值;势垒的宽度越大或势垒的高度越小,即势垒的斜率越小(势垒越平缓)时,相位时间和驻留时间的峰值越大;同时随着势垒高度的增加或者势垒宽度的增加,透射相位时间和驻留时间的峰值都会向右(k增加的方向)移动,但对于相位时间和驻留时间不同的是:相位时间的峰值一般出现
处,而驻留时间的峰值则一般出现在
处。