函数的水平集

The Level Sets of Functions

摘要: 本文利用函数的水平集给出函数的一些基本性质的刻画，包括函数凸性、连续性、可测性、可积性以及一些重要的应用。我们发现，在一定意义下，函数的性质完全由其水平集决定，而且方法上较为统一和直观。

Abstract: In this paper, we give some properties of functions by level sets of functions, including convexity, continuity, measurable, integrability and some important applications. We find that the properties of a function are completely determined by its level set, and the methods are uniform and intuitive.

1. 引言

数学分析是一门很基础且很重要的专业学科，数学分析研究的对象是函数，主要研究函数(包括泛函)的一些基本性质，包括凸性、连续性、可微性、可积性以及一些积分估计等。研究这些性质的方法多种多样，国内也有很多很优秀经典的教材 [1] [2] [3] [4]。水平集方法在现实中有广泛的应用，例如图像分割 [5]，计算机视觉 [6] 等领域。然而，介绍水平集方法的几乎都是相应学科的专著。鉴于水平集的重要性，本文主要通过总结和归纳由函数的水平集给出函数性质的刻画。我们发现，在一定意义下，函数的性质完全由其水平集决定，方法上较为统一和直观，而且可读性强。然而，本科数学分析的教材很少涉及这方面的内容。这是写这篇文章的主要动机和意义。

2. 一些定义

我们首先给出一些基本定义，这些定义在正文中经常用到。

定义2.1. 设 $f:\Omega \to R$ 是 $\Omega$ 上的实值函数，对每个 $t$，我们定义函数上水平集为

$S_f\left(t\right)=\left\{x\in \Omega :f\left(x\right)>t\right\}$.

定义函数的下水平集为

$L_f\left(t\right)=\left\{x\in \Omega :f\left(x\right)\le t\right\}$.

上水平集和下水平集我们统称函数的水平集。

定义 2.2. 一个由 $\Omega$ 的某些子集构成的集合 $\Sigma$，如果满足下面几条公理，则称它是一个 $\sigma$ 代数：

i) 若 $A\in \Sigma$，则 $A^c\in \Sigma$，

ii) $A_1,A_2\cdots$ 是 $\Sigma$ 中的一可数的集合族，则它的可数并 $\underset{i=1}{\overset{\infty }{\cup }}{A}_i\subset \Sigma$，

iii) $\Omega \subset \Sigma$。

定义2.3. 测度空间是由三部分组成：集合 $\Omega$， $\sigma \text{-}$ 代数 $\Sigma$ 及测度 $\mu$。我们通常把 $\Sigma$ 中的元素称为可测集

定义2.4. 设 $A\subset R^n$ 是Lebesgue 测度有限的Borel集(由开集生成的最小 $\sigma$ 代数)。我们定义集合 $A$ 的对称重排 $A^{\ast }$ 为

$A^{\ast }=\left\{x:\left|x\right|<r\right\},其中\left(\left|S^{n-1}\right|/n\right)r^n=L^n\left(A\right)$,

这里， $\left|S^{n-1}\right|$ 表示 $S^{n-1}$ 的表面积。

定义2.5. 设 $A$ 是一个集合，定义集合 $A$ 的特征函数为

${\chi }_A\left(x\right)=\{\begin{array}{l}1x\in A\\ 0x\notin A\end{array}$

3. 函数的一些性质的水平集刻画

这一部分我们主要从函数的水平集的角度给出函数的一些基本性质的刻画。

3.1. 函数本身的刻画

我们可以利用函数的水平集的直接构造出函数本身。

性质3.1.1 (层饼表示定理)设 $f\left(x\right)$ 是任意的非负可测函数，则有

$f\left(x\right)={\displaystyle {\int }_0^{\infty }{\chi }_{\left\{f>t\right\}}\left(x\right)\text{d}t}.$

证明：这是显然的，实际上

$\begin{array}{c}{\displaystyle {\int }_0^{\infty }{\chi }_{\{f>t\}}}\left(x\right)\text{d}t={\displaystyle {\int }_0^{f(x)}1\text{d}t+{\displaystyle {\int }_{f(x)}^{\infty }0\text{d}t}}\\ =f\left(x\right).\end{array}$

这个性质在实际应用中极其有用，因为它允许我们在很多情况下把处理一个普通函数的积分简化为处理特征函数的积分(利用Fubini定理)。

3.2. 函数的凸性

我们首先给出凸集和凸函数的定义。

定义3.2.1. 我们称集合 $A$ 为凸集，若对任意的 $x,y\in A,\theta \in \left[0,1\right]$，有

$\theta x+\left(1-\theta \right)y\in A$.

定义3.2.2. 若 $f$ 的定义域为凸集，我们称 $f$ 是凸函数，若其满足

$f\left(\theta x+\left(1-\theta \right)y\right)\le \theta f\left(x\right)+\left(1-\theta \right)f\left(y\right)，其中x,y\in domf，\theta \in \left[0,1\right].$

这里 $domf$ 表示函数的定义域。

由函数凸性的定义，我们马上得到凸函数的必要条件：

性质3.2.1.凸函数的下水平集是凸集，但是反之不一定成立。

证明：设任意的的 $t$， $x,y\in L_f\left(t\right)$，我们有

$\begin{array}{c}f\left(\theta x+\left(1-\theta \right)y\right)\le \theta f\left(x\right)+\left(1-\theta \right)f\left(y\right)\\ \le \theta t+\left(1-\theta \right)t\\ \le t.\end{array}$

因此

$\theta x+\left(1-\theta \right)y\in L_f\left(t\right).$

另一方面，我们很容易验证函数 $f\left(x\right)=-{\text{e}}^x$ 的任意下水平集是凸的，但是这个函数不是凸的。然而，这个性质的可以判断一个集合是否是凸集：若某个集合可以描述为一个凸函数的下水平集，那么这个集合为凸集。

这个结论虽然不能从函数的水平集的凸性直接得到函数的凸性，但是我们可以从函数的图像(Epigraph)的角度上看，可以得到函数凸性的一个充分必要条件。

定义3.2.3. 设 $f:R^n\to R$。我们定义 $f$ 的图像(Epigraph)为

$Epif=\left\{\left(x,t\right)\in R^{n+1}|x\in domf,f\left(x\right)\le t\right\}.$

由这个定义，我们可以得到函数的凸性的一个充要条件：

性质3.2.2. 函数 $f$ 为凸函数当且仅当其图像为凸集。

证明：根据定义，这是显然的。

注：对于凹函数，相关的性质也可以用水平集刻画，只要把下水平集改为上水平集即可。

3.3. 函数的连续性

因为 $\left\{\left(-\infty ,b\right):b\in R\right\}\cup \left\{\left(a,+\infty \right):a\in R\right\}$ 为 $R$ 上的一组拓扑子基，我们很容易验证：

性质3.3.1. 对应任意的 $t$，若函数的水平集 $S_f\left(t\right)=\left\{x\in \Omega :f\left(x\right)>t\right\}$ 是开的，则函数 $f\left(x\right)$ 是下半连续的。

类似的，我们可以得到函数的上半连续的刻画：

性质3.3.2. 对应任意的 $t$，若函数的水平集 ${\tilde{L}}_f\left(t\right)=\left\{x\in \Omega :f\left(x\right)<t\right\}$ 是开的，则函数 $f\left(x\right)$ 是上半连续的。

性质3.3.3. 如果一个函数既是上半连续，也是下半连续，那么它一定连续。

3.4. 函数的可测性

我们可以直接根据函数的水平集给出可测函数的定义：

定义3.4.1.对应任意的 $t$，若函数的上水平集 $S_f\left(t\right)=\left\{x\in \Omega :f\left(x\right)>t\right\}$ 是可测集，则称函数 $f\left(x\right)$ 是可测的。更一般地，如果 $f:\Omega \to C$ 是复函数，那么当它的实部 $\mathrm{Re}f$ 和虚部 $\mathrm{Im}f$ 都是可测函数时，称 $f$ 可测。

从水平集的角度去定义函数的连续和可测性，我们可以得到可测函数与连续函数的某些关系。例如，如果 $\Sigma$ 取 $R^n$ 上的Borel- $\sigma$ 代数B，则显然每个连续函数都是Borel可测的，此时函数的水平集

$S_f\left(t\right)=\left\{x\in \Omega :f\left(x\right)>t\right\}$ 是开集。实际上，上半连续或下半连续函数都是Borel可测的。下半连续函数的可测性是显然的，关于上半连续函数的可测性，因为集合 $\left\{x|f\left(x\right)<t+\frac{1}{i}\right\}$ 是可测的，同时

$\left\{x\in \Omega |f\left(x\right)\le t\right\}=\underset{i=1}{\overset{\infty }{\cap }}\left\{x|f\left(x\right)<t+\frac{1}{i}\right\},$

所以 $\left\{x\in \Omega |f\left(x\right)\le t\right\}$ 是可测的，从而可以得到上半连续的函数的可测性。

通过上面的分析，我们如果从水平集的角度研究函数的连续性与可测性之间的关系，实际上建立一种 $\sigma$ 代数和拓扑之间的关系的。从这个角度看，这是有意思的。

3.5. 函数的可积性

为了简单起见，本部分都假设 $f$ 是非负的可测函数，且直接讨论一般测度 $\mu$ 上的积分。函数的可积性只取决于函数大的值的集合究竟有多大，而以这些大的值在哪里取到没有什么关系。因此，我们很自然可以考虑对应大的 $t$，水平集的测度究竟多大。由此直接引出可测函数的分布函数的定义。我们记：

$F_f\left(t\right)=\mu \left(S_f(\; t\; )\right)$

也就是说 $F_f\left(t\right)$ 是使得 $f>t$ 的集合的测度。我们把这个函数称为 $f$ 的分布函数 [7]。显然， $F_f\left(t\right)$ 关 $t$ 是单调不增的。因此我们可以用Riemann积分 ${\displaystyle {\int }_0^{\infty }{F}_f}\left(t\right)\text{d}t$ 来定义 $f$ 在 $\Omega$ 上的积分：

.

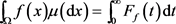利用这个定义，我们把层饼表示定理推广为：

性质3.5.1. [8] 设 $v$ 为正实半轴上Borel集上的测度，使得 $\phi \left(t\right)=v\left(\left[0,t\right)\right)$ 对每个 $t>0$ 均有限。再设 $\left(\Omega ,\Sigma ,\mu \right)$ 为一个测度空间且 $f\left(x\right)$ 是任意的非负可测函数，那么有

证明：为了读者的方便，我们把文献 [8] 中关于此定理的证明摘录于此。根据定义，我们有

${\displaystyle {\int }_0^{\infty }\mu \left(S_f\left(t\right)\right)}v\left(\text{d}t\right)={\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_{\Omega }{\chi }_{f>t}\left(x\right)}}\mu \left(\text{d}x\right)v\left(\text{d}t\right)$.

利用Fubini定理，(3.5)的右端等于

${\displaystyle \underset{\Omega }{\int }\left({\displaystyle {\int }_0^{\infty }{\chi }_{\{f>t\}}\left(x\right)}v\left(\text{d}t\right)\right)\mu \left(\text{d}x\right)}$.

注意到

${\displaystyle {\int }_0^{\infty }{\chi }_{\text{{}f>\text{t}}}}\left(x\right)v\left(\text{d}t\right)={\displaystyle {\int }_0^{f(x)}v\left(\text{d}t\right)=\phi \left(f\left(x\right)\right)}$,

结论成立。

上述的结论说明函数的可积性完全由其分布函数决定。因此，通过研究函数的水平集，我们完全可以弄清楚可测函数的可积性，而且相对比较自然和直观。

与分布函数密切相关的一个概念：函数的重排。直观上看，分布函数与函数的重排是一对“互逆”函数。函数的可积性完全可以由他们决定。有意思的是，通过对函数重排，得到一些非常有用的积分不等式。例如，根据重排不等式，我们可以得到著名的等周不等式。为了定义函数的重排，我们首先给出特征函数的重排的定义，即：

${\chi }_A{}^{\ast }={\chi }_{A^{\ast }}$

现在假设 $f$ 是一个无穷远处趋于零的Borel可测函数，定义 $f$ 的重排函数为

$f^{\ast }\left(x\right)={\displaystyle {\int }_0^{\infty }{{\displaystyle \chi }}_{{}_{\left\{\left|f\right|>t\right\}}}^{\ast }\left(x\right)\text{d}t}.$

函数的重排一个重要的性质就是重排函数 $f^{\ast }$ 与函数 $f$ 就有相同的分布函数，因此，函数的可积性完全由他们决定，这些概念都是从函数的水平集的基础上给出，而且具有很好的性质。从这个方面看，用水平集研究函数的性质具有一定的优越性。

4. 水平集的一些应用

4.1. 几个基本定理

根据层饼表示定理，我们很容易把数学分析中的黎曼积分中极限与积分交换次序的几个重要定理推广到一般的测度空间上。

定理4.1.1 [8] (单调收敛定理)设 $f_1,f_2,\cdots ,f_n\cdots$ 是测度空间 $\left(\Omega ,\Sigma ,\mu \right)$ 上递增的可测函数列，且

$\underset{n\to \infty }{\lim }{f}_n\left(x\right)=f\left(x\right),\mu \text{-a}.e.x\in \Omega ,$

则

$\underset{n\to \infty }{\text{lim}}{\displaystyle \underset{\Omega }{\int }{f}^n}\left(x\right)\mu \left(\text{d}x\right)={\displaystyle \underset{\Omega }{\int }f}\left(x\right)\mu \left(\text{d}x\right).$

证明：不失一般性，我们假设 $f_n$ 非负。显然， $S_f\left(t\right)=\underset{n=1}{\overset{\infty }{\cup }}{S}_{f_n}\left(t\right)$，由测度的连续性，我们可以得到

$\underset{n\to \infty }{\lim }{F}_{f^n}\left(t\right)=F_f\left(t\right).$

根据一般测度空间上的可测函数积分的定义，我们只需要验证Riemann积分满足

$\underset{n\to \infty }{\text{lim}}{\displaystyle {\int }_0^{\infty }{F}_{f_n}}\left(t\right)\text{d}t={\displaystyle {\int }_0^{\infty }{F}_f}\left(t\right)\text{d}t$.

由于每个分布函数 $F_{f^n}\left(t\right)$ 关于 $t$ 和 $n$ 都是单调的，所以结论显然成立。证明完毕。

作为单调收敛定理的推论，我们很容易得到在一般测度空间的上的Fatou引理和控制收敛定理。

4.2. 水平集在变分法中的应用

无穷维的临界点理论在在微分方程解的存在性的证明中起到很重要的作用，其已经发展成为一门很重要的独立分支。而建立Morse理论、山路定理及更一般的环绕定理等临界点理论，一个主要的思想是主要考虑了泛函水平集的拓扑结构的变化。设 $X$ 是Banach空间， $f\in C^1\left(X,R\right)$。

记 $\kappa =\left\{u\in X|f^{\prime }\left(u\right)=0\right\}$， $K_c=\kappa \cap f^{-1}\left(c\right)$。

定义4.2.1. 设 $c\in R$，称 $\left\{u_n\right\}\subset X$ 为 $f\in C^1\left(X,R\right)$ 的 ${\left(PS\right)}_c$ 序列，若

$f\left(u_n\right)\to c,f^{\prime }\left(u_n\right)\to 0.$

称 $f$ 满足 ${\left(PS\right)}_c$ 条件，若它的任意 ${\left(PS\right)}_c$ 序列都存在收敛子列。若对任意的 $c\in R$， $f$ 都满足 ${\left(PS\right)}_c$ 条件，则称 $f$ 满足 $\left(PS\right)$ 条件。

下面的定理表明，若水平集 $f^{-1}\left[a,b\right]$ 中没有 $f$ 的临界点，则 $L_f\left(a\right)$ 是 $L_f\left(b\right)$ 的强形变收缩核。具体证明可以参考文献 [9]。

定理4.2.1.设 $f\in C^1\left(X,R\right)$ 满足(PS)条件，若 $f^{-1}\left[a,b\right]\cap \kappa =\varnothing$，则存在 $\eta \in C\left(\left[0,1\right]\times L_f\left(a\right),L_f\left(b\right)\right)$ 使得

i) $\eta \left(0,·\right)={\chi }_{L_f(b)},\eta \left(1,L_f\left(b\right)\right)\subset L_f\left(a\right)$，

ii) $\eta \left(t,x\right)=x,\forall \left(t,x\right)\in \left[0,1\right]\times L_f\left(a\right)$。

若 $a$ 是 $f$ 的临界点，上述定理可以推广为

定理4.2.2. 设 $f\in C^1\left(X,R\right)$ 满足(PS)条件， $f$ 只有有限的临界点。 $a$ 是 $f$ 在 $\left[a,b\right)$ 上唯一的临界值。则存在 $\eta :\left[0,1\right]\times \left(L_f\left(a\right)\backslash L_f\left(b\right)\right)\to L_f\left(b\right)\backslash {\kappa }_b$ 使得

i) $\eta \left(0,·\right)={\chi }_{L_f(b)\backslash {\kappa }_b}$，

ii) $\eta \left(t,x\right)=x,\forall \left(t,x\right)\in \left[0,1\right]\times L_f\left(a\right)$，

iii) $\eta \left(1,L_f\left(b\right)\backslash {\kappa }_b\right)\subset L_f\left(a\right)$。

注：这个定理是建立Morse不等式的关键。

5. 结论

本文研究函数水平集对函数性质刻画，同时也给出了函数水平集一些简单但重要的应用。在一定意义下，函数的性质完全由其水平决定，而且方法上较为统一和直观。另外一方面，函数水平集在计算机视觉理论，图像分割等实际问题当中都有着广泛的应用，鉴于这两点，我们建议在本科数学专业加入关于水平集这一部分的内容。

基金项目

本文受到国家自然科学资金青年资金项目(11701114)资助。

NOTES

^*通讯作者。