基于OpenFOAM的槽道内液态金属湍流换热直接数值模拟

Direct Numerical Simulation on Heat Transfer of Liquid Metal in Channels Based on OpenFOAM

摘要: 液态金属被广泛用作先进核能系统的一回路冷却剂。液态金属的普朗特数较低，其换热特征与常规流体区别较大。本文采用OpenFOAM对槽道内液态金属湍流换热过程进行了直接数值模拟。模拟采用的摩擦雷诺数为180，分子普朗特数分别为1，0.71，0.25，0.125，0.05，0.025，0.005，0.001。通过与前人研究的数值结果进行对比，验证了本文模型的准确性。分析了普朗特数对温度分布的影响，随着普朗特数的降低，常见的温度分布对数律区在截面内的占比明显减小。采用指数函数对截面内的无量纲温度分布进行拟合，得到了普朗特数在0.001到1范围内的温度分布计算式。结合速度幂律，在温度分布公式的基础上推导出了努赛尔数关系式。

Abstract: The liquid metal is widely used as the primary coolant in many advanced nuclear systems. Due to the low Prandtl number, the turbulent heat transfer characteristics of liquid metal are different from the conventional fluids. Using the method of Direct Numerical Simulation (DNS), turbulent convection of liquid metal is simulated with OpenFOAM. The friction Reynolds number is 180. The molecular Prandtl numbers (Pr) are 1, 0.71, 0.25, 0.125, 0.05, 0.025, 0.005 and 0.001. The accuracy of present numerical model is validated by comparing with the numerical results of previous stud-ies. Prandtl number effects on temperature distribution are analyzed. The region of logarithmic law for temperature in the cross section is decreased with the decreasing of Prandtl number. Exponent functions for dimensionless temperature distribution in the cross section are obtained by regres-sion analysis of numerical results with 0.001 ≤ Pr ≤ 1. Combined with the power law for dimension-less velocity distribution, the Nusselt number correlation for turbulent convection of liquid metal is derived.

1. 引言

液态金属的导热系数极大，具有更高的分子热扩散系数。相比于水和空气等常见冷却工质，液态金属的普朗特数(Pr)要小两个数量级。液态金属的对流换热特性与常规流体有较大区别。在液态金属的湍流换热过程中，近壁区的导热主导区厚度远大于粘性底层厚度，导热对于传热的贡献更大。准确预测冷却剂在近壁区的湍流换热过程对于反应堆安全至关重要。准确的传热关联式对于热交换器的设计十分重要。直接数值模拟(DNS)是对N-S方程进行直接求解的方法，不附加湍流模型，对时间空间完全解析。DNS具有很高的精度，能够获取速度场与温度场的精细特征。Komen [1] 等人采用OpenFOAM对槽道和圆管内湍流流动进行了准DNS模拟。本文通过与谱方法和有限差分方法的数值结果进行对比，证明了使用OpenFOAM进行直接数值模拟的可行性。Kim [2] 使用直接数值模拟的方法研究槽道湍流被动标量场，研究了普朗特数(0.1, 0.71, 2)对槽道湍流换热特性的影响。Kawamura [3] [4] [5] 等人采用直接数值模拟的方法模拟不同普朗特数(0.025, 0.1, 0.2, 0.05, 0.71, 2)在槽道内的湍流换热过程，分析了等热流条件下湍流换热中的雷诺数和普朗特数效应。Tiselj [6] 对普朗特数低至0.01的液态钠进行了DNS模拟，模拟采用的摩擦雷诺数为180，395和590。

虽然液态金属湍流换热的相关研究较多，但已有研究所选取的普朗特数范围大多在0.01到2之间 [2] - [8]。本文采用基于有限体积法的OpenFOAM-7对槽道内液态金属的湍流换热过程进行直接数值模拟。流动的摩擦雷诺数为180。为分析低普朗特数流体在槽道湍流中的分布特征，建立对流换热关系式，普朗特数范围为0.001~1。得到了8种Pr (1, 0.71, 0.25, 0.125, 0.05, 0.025, 0.005, 0.001) 工况下无量纲温度场分布。采用Pr为1，0.71，0.05，0.025的模拟结果与已有数据库 [3] [4] [5] 进行比较，以验证本文模型的准确性。分析了低普朗特数下槽道湍流的换热特征，拟合得到Pr为0.001到1温度分布幂律公式。最后根据温度分布公式，推导出努赛尔数(Nu)的换热关系式。

2. 数值模型

2.1. 控制方程及边界条件

流动为不可压缩流体的充分发展湍流，且不考虑重力。标量传输过程视为被动输运，不影响速度分布。所有流体的物性都视作常数。质量，动量和能量方程的表达式如式(1)。

$\begin{array}{l}\frac{\partial u_i}{\partial x_i}=0\\ \frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}=-\frac{1}{\rho }\frac{\partial p}{\partial x_i}+\nu \frac{{\partial }^2{u}_i}{\partial x_j\partial x_j}+\beta \\ \frac{\partial \stackrel{⌢}{T}}{\partial t}+u_i\cdot \nabla \stackrel{⌢}{T}-\nabla \cdot \left(\alpha \nabla \stackrel{⌢}{T}\right)+uS=0\end{array}$ (1)

$\beta$ 为动量源项。采用Vlilliers [9] 方法生成充分发展湍流初始场。在槽道的上下壁面，速度场和压力场分别使用无滑移边界条件和零梯度边界条件，温度场边界条件为等热流密度。为节省计算资源，速度场和温度场在流向和展向上都使用了周期性边界条件。Patankar [10] 提出了将瞬时温度T分解为周期性部分 $\stackrel{⌢}{T}$ 和非周期性的S。S为流向的温度梯度，由能量守恒关系式(2)计算：

$S=\frac{T\left(x+L\right)-T\left(x\right)}{L}=\frac{\Delta T}{L}=\frac{q_w}{\rho c_p{u}_{mean}\delta }$ (2)

$T=\stackrel{⌢}{T}+S$ (3)

u为流向速度，c_p为定压比热容，q_w为壁面热通量， $\rho$ 为液体密度。 $u_{mean}$ 定义为式(4)。摩擦雷诺数的定义为式(5)。普朗特数的定义为式(6)，其中 $\lambda$ 为热导率。

$u_{mean}=\frac{1}{\delta }{\displaystyle {\int }_0^{\delta }u\text{d}y}=\frac{1}{\delta }{\displaystyle \underset{i}{\overset{\delta }{\sum }}{u}_i\Delta y_i}$ (4)

$R{e}_{\tau }=\frac{u_{\tau }\delta }{\nu }$ (5)

$Pr=\frac{\nu }{\alpha }=\frac{\nu }{\lambda /\rho c_p}$ (6)

通过在pisoFoam中添加温度方程，求解得到周期性温度。在整个流体域中，总的热量增加由槽道壁面的热传导引入，通过式(2)，式(4)和式(6)，结合傅里叶导热定律可计算得到流向温度梯度的大小，见表1。

Table 1. Value of temperature gradient

表1. 温度梯度值

2.2. 离散格式

OpenFOAM使用具有二阶精度的有限体积法。在本次计算中，使用的离散格式均为二阶，Komen [1] [11] 等人验证了使用二阶精度离散格式进行直接数值模拟的可行性。对于时间瞬态项的离散，采用二阶隐式向后差分格式backward。压力和粘性项采用二阶精度的Gauss linear格式。对流项采用二阶迎风格式离散。标量输运方程中的对流项采用迎风和二阶中心差分的混合格式LUST。速度和压力采用PISO算法进行解耦计算。

2.3. 几何模型和网格

选取的几何模型如图1所示。x，y，z方向上的尺寸分别为6.4δ，2δ，3.2δ，δ为槽道的半高宽。该模型为Kawamura [5] 所使用的最小模型。

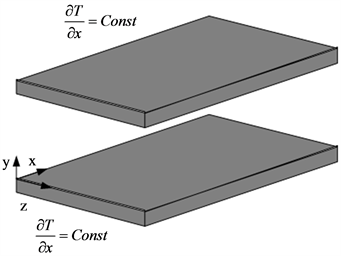
Figure 1. The geometry of computational domain

图1. 计算域几何模型

在流向和展向上使用均匀分布的网格。壁面法向采用非均匀网格，伸展比为1.05。Komen [1] 采用Kawamura计算使用的最粗糙网格，评估了使用OpenFOAM进行DNS计算的数值耗散，计算结果与已有DNS数据库符合较好。相比于Komen [1]，本次计算在壁面方向采用更多网格点以保证计算精度。标量耗散的尺度为Batchelor尺度，与Pr成反比。因此适用于普朗特数为1的网格同样适用于普朗特数小于1的工况。计算参数总结在表2中。

Table 2. Summary of computational parameters

表2. 计算参数总结

3. 结果与讨论

本节针对摩擦雷诺数为180，8种Pr工况，研究了液态金属湍流换热的低普朗特数效应。本文3.1节将数值结果中的时均速度场和湍流脉动强度与已有数据库进行了对比，以验证模型的准确性。3.2节给出了8种Pr工况下的无量纲温度场分布，分析了普朗特数对槽道湍流的换热特征的影响。拟合出了Pr为0.001到1时截面内温度分布的幂律。3.3节根据温度分布与Pr关系，得出了努赛尔数Nu的换热关系式。

3.1. 模型验证

将时均速度场计算结果与前人DNS数据库 [3] [12] 进行对比，结果与数据库符合较好，见图2。其中无量纲壁面距离和无量纲速度由公式(7)计算。

Figure 2. Profile of mean velocity

图2. 时均速度分布

$u^{+}=u/u_{\tau },y^{+}=u_{\tau }y/\nu ,u_{\tau }=\sqrt{{\tau }_w/\rho }$ (7)

将瞬时速度分解为时均速度 ${\bar{u}}_i$ 和脉动速度 ${u^{\prime }}_i$，见式(8)。

$u_i={\bar{u}}_i+{u^{\prime }}_i$ (8)

湍流脉动强度定义为式(9)。湍流脉动强度的对比如图3所示。与Kawamura数据库的最大相对误差为5.2%，分别为4.6%和5.6%，而三个脉动量与Vreman数据库的误差都在5%以内。

$u_{rms}^{+}=\frac{\sqrt{u^{\prime }{u}^{\prime }}}{u_{\tau }},v_{rms}^{+}=\frac{\sqrt{v^{\prime }{v}^{\prime }}}{u_{\tau }},w_{rms}^{+}=\frac{\sqrt{w^{\prime }{w}^{\prime }}}{u_{\tau }}$ (9)

3.2. 温度场及拟合

为分析液态金属的低Pr效应，本节比较同一摩擦雷诺数不同Pr工况下的温度分布。引入无量纲温度定义式(10)，以及摩擦温度定义式(11)。

${\theta }^{+}=\left(T_w-T\right)/T_{\tau }$ (10)

$T_{\tau }=\frac{q_w}{\rho c_p{u}_{\tau }}$ (11)

Figure 3. Profile of $u_{rms}^{+}$, $v_{rms}^{+}$, $w_{rms}^{+}$

图3. $u_{rms}^{+}$， $v_{rms}^{+}$， $w_{rms}^{+}$ 分布

Figure 4. Mean temperature profiles of Pr vary from 0.001 to 1

图4. Pr为0.001到1的时均温度分布

Pr为0.025，0.05，0.71和1的无量纲化温度与Kawamura的DNS数据库进行了对比，误差小于5%。如图4所示，随着普朗特数的降低，温度在整个截面上都会受到分子热扩散系数的影响，造成其与常规流体(Pr~1)的温度分布区别较大。温度随壁面距离梯度变化不大，而常规流体在靠近壁面区域的温度梯度变化很大，之后趋于平缓。

图5所示，在普朗特数为1时温度和速度的分布相近，粘性底层与导热主导区的厚度相近。对比Pr数的温度分布，Pr数越小，温度分布曲线趋于平缓。这是由于随着Pr数的降低，分子导热在对流换热中占到主导地位，导致其符合对数律温度分布的 $y^{+}$ 范围不断缩小。继续使用对数律温度分布来计算低普朗特数流体的换热系数，将会造成极大的误差，所以对于液态金属的传热关联式，需要新的温度分布计算式。本文采用指数函数式(12)对计算结果进行拟合，得到的温度分布关系式见表3。

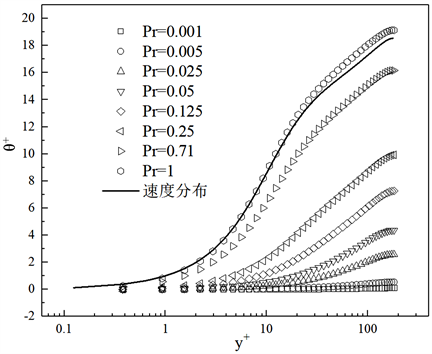
Figure 5. Comparison of mean temperature profile and velocity profile

图5. 时均温度场与速度场对比

${\theta }^{+}=a\cdot {\left(y^{+}\right)}^b$ (12)

Table 3. Fitting result of temperature profile

表3. 温度分布拟合结果

如图6所示， $y^{+}>30$ 时所拟合函数与数值结果符合较好，能很好的预测Pr范围为0.001到1的温度分布。从表3拟合结果中可以得出，式(12)中的系数a随着Pr数增加而增加，系数b随着Pr数增加而减小。分别采用式(13)和(14)的对a、b与Pr的关系进行拟合。

$a=c_{1}P{r}^{c_2}$ (13)

$b=c_3/\ln \left(Pr+c_4\right)$ (14)

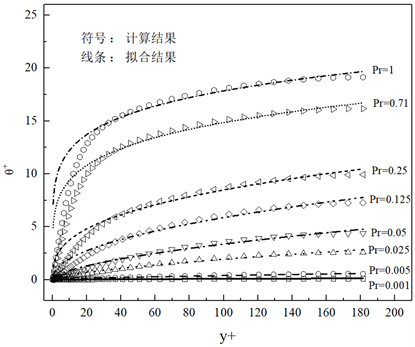
Figure 6. Fitting results of different Prandtl numbers

图6. 不同普朗特数拟合结果

由此，普朗特数范围为0.001到1内，温度分布关系式为式(15)。

${\theta }^{+}=\left(8.506P{r}^{1.146}\right){\left(y^{+}\right)}^{0.1311/\ln \left(Pr+1.199\right)}$ (15)

3.3. 液态金属努赛尔数换热关系式

采用幂律形式的速度分布式(16)，计算槽道内平均速度，结果见式(17)。

$u^{+}=c{\left(y^{+}\right)}^d$ (16)

$u_{mean}=\frac{1}{\delta }{\displaystyle {\int }_0^{\delta }u\text{d}y}=\frac{c{u}_{\tau }}{\text{1+}d}{\left(\frac{u_{\tau }}{\nu }\right)}^d{\delta }^d$ (17)

带入摩擦速度的定义式 $u_{\tau }=\sqrt{{\tau }_w/\rho }$，并根据平均速度(17)计算阻力系数f，见式(18)。

$f=8{\left[\frac{1+d}{c}{\left(\frac{u_{mean}\delta }{\nu }\right)}^{-d}\right]}^{\frac{2}{d+1}}$ (18)

结合式(12)的温度分布形式和式(16)的速度分布形式，求解槽道内的壁面温度 $T_w$ 与体平均温度 $T_b$ 的温差见式 。

$T_w-T_b=\frac{{\displaystyle {\int }_0^{\delta }u\left(T_w-T\right)\text{d}y}}{u_{mean}\delta }$ (19)

带入摩擦速度 $u_{\tau }$ 和努塞尔数( $Nu=h\delta /\lambda$ )定义，化简体平均温度公式(20)，最终得到Nu换热关系式(21)。

$Nu=\frac{\left(b+d+1\right)}{a\left(\text{1+}d\right)}\frac{Pr}{R{e}^{b-1}}{\left(\frac{f}{8}\right)}^{-\frac{b-1}{2}}$ (20)

式(21)中雷诺数Re基于槽道半高宽 $\delta$。其中， $a=8.506P{r}^{1.146}$， $b=0.1311/\ln \left(Pr+1.199\right)$，为表4中系数拟合结果。针对中等雷诺数，d取值1/7 [13]。

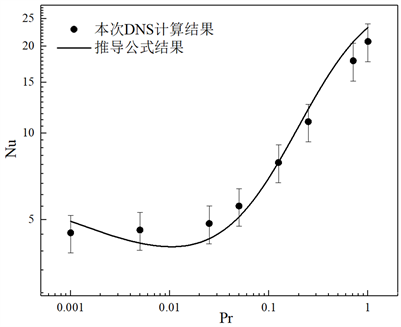
Figure 7. Comparison of derived Nu equation with DNS result at Re = 5670

图7. Re = 5670时，推导得到Nu公式与DNS结果比较

Table 4. Coefficient relationship fitting result

表4. 系数关系式拟合结果

在Re为5670，Pr范围为0.001到1的情况下，对比推导得到的Nu换热关系式(21)与本次DNS计算结果，如图7所示。公式推导结果计算得到的Nu与本次DNS计算结果在15%误差内。

4. 结论

本文利用OpenFOAM对槽道内液态金属湍流换热过程进行了直接数值模拟，得到结论如下：

1) Pr为1时速度分布于温度分布相近，Pr小于1时，符合对数律温度分布的y⁺值范围随Pr的降低而缩小。

2) 采用幂指数形式，拟合得到了普朗特数范围为0.001到1的温度分布。

3) 根据拟合得到温度分布关系式，推导出了Re为5670，Pr范围为0.001到1的情况下的努赛尔数换热关系式。

基金项目

国家自然科学基金资助项目(No. 51906068)中央高校基本科研业务费专项资金资助(2020MS032)。

参考文献

NOTES

^*通讯作者。