1. 引言
齿轮传动在工程中有大量的应用背景。在齿轮系统的研究中,Chang等人 [1] 研究了单自由度直齿圆柱齿轮系统有或没有非线性悬挂的动力学行为。Chang和Cai [2] 在非线性悬挂、油膜力和齿轮啮合力的情况下,对齿轮轴承系统的动力学行为进行分析。Farshidianfar和Saghafi [3] 利用Melnikov方法研究了一类非线性齿轮系统的全局同宿分岔和混沌行为的变迁。Gou等人 [4] 在简单单元映射法和逃逸时间算法的基础上,设计了一种改进算法,对扭振齿轮多参数耦合系统的各个状态单元和动态特性进行了检测。还有Hotait和Kahraman [5] 提供一套全面的实验数据,包括同时从同一齿轮收集到的动态应力因子和动态传输误差值,以补充早期的耐久性和噪声指标之间的关系理论研究。另外Liu等人 [6] 为基于单元映射法的齿轮系统振动控制和参数设计提供了依据,验证了理解域边界分析方法的有效性。Xiang等人 [7] 对时变刚度、齿隙和表面摩擦的齿轮轴承系统进行系统动力学分析。提出了一种周期展开法,建立了一副直齿圆柱齿轮的六自由度非线性动力学模型。李大鹏等 [8] 研究含有单向离合器以及张紧轮的轮–带传动系统的稳定稳态周期响应。并运用 Runge-Kutta方法直接数值求解系统的时间历程,进而对比验证基于谐波平衡法得到的稳态响应分析结果。近年来,Shi等人 [9] 根据安全区域对安全盆及其侵蚀对齿轮传动系统进行了数值计算。Gou等人 [10] 建立了齿轮–转子–轴承系统的五自由度非线性动力学模型,该系统由一对齿轮支承轴、轴承及其他辅助部件组成。Wei等人 [11] 建立了不确定单级齿轮传动系统的动力学模型,并且首次设计实现了一种不确定单级正齿轮传动系统的试验台。
在带有扰动参数系统中,我们一般使用快慢分析方法进行研究。Rinzel等人 [12] [13] 引入了快慢分析方法,其基本思想是将一个多时间尺度的系统分为快子系统(FS)和慢子系统(SS),并将慢变变量视为慢变分岔参数,可以清楚地解释其簇发机理。当所有变量表现出小振幅振荡或保持不变时,FS处于静止状态(QS),而所有变量表现出大振幅振荡,则FS对应于一个尖峰状态(SP)。当慢子系统(SS)影响快子系统(FS)时,导致QS和SP之间的转换,簇发振荡因此产生。
此外,有大量的学者对非光滑动力系统研究中,并有一套完整的研究体系。比如,Qu等人 [14] 基于混沌地磁场模型探讨具有参数激励和外激励的Filippov型系统的簇发振荡模式和非光滑动力学行为。Zhang等人 [15] 引入一个非光滑因子,探讨具有多时间尺度系统的复杂动力学行为。Qu等人 [16] 基于一个典型的Chua电路研究了多尺度频域对右侧不连续Filippov系统复杂振荡的影响。Wang等人 [17] 引入具有分段特性的非线性电阻器和谐波变化的电源,建立了在频域内存在两个尺度耦合的修正的非光滑系统模型。然后探讨了两尺度耦合对非光滑系统动力学的影响。Huang等人 [18] 提出了一种具有多个共存吸引子的三维混沌系统,其中调节一个参数的值可以驱动混沌行为从单涡旋吸引子演化为双涡旋吸引子。Wang等人 [19] 研究了一个具有分段非线性电阻和慢变周期激励的典型Chua电路,研究了分段光滑动力系统中簇发振荡的动力学机制。
本文分为以下几个部分。在第二节中,简单地描述齿轮系统的运动方程;在第三节中,讨论不同区域的平衡点和稳定性;第四节讨论了非传统的分岔分析;第五节结合分岔图对系统的相关参数进行了分析;第六节分析了该系统引起的簇发振荡现象及其机理;最后对本文进行总结。
2. 齿轮系统的方程描述
单级直齿圆柱齿轮系统的非线性动力学模型如图1,
为两齿轮的扭转振动位移;
为两齿轮的转动惯量;
为两齿轮的扭矩;
为两齿轮的半径。考虑了时变刚度、侧隙和综合传动误差这几个重要的非线性因素,单级直齿圆柱齿轮系统的无量纲方程如下 [9]:
(1)

Figure 1. Simplified physical model of the spur gear transmission system
图1. 直齿圆柱齿轮传动系统的简单物理模型
在方程(1)中,x,
,
分别代表齿轮传动系统中的位移,速度,加速度。F是无量纲转矩,k是无量纲的啮合刚度,
是无量纲的啮合频率,t是无量纲时间。此外,
是非线性间隙函数,
是内部误差激励函数。
的表达形式如下:
(2)
在上式中,b是一齿侧间隙的一半。应用快慢分析方法 [12] [13],我们可以将快子系统表示为一个自治形式,而不连续的分岔可以用Clarke的广义雅可比矩阵来讨论。在方程(1)中假设
,
,并给出自治方程(快子系统),
(3)
其中,
是用非光滑或分段光滑的特征来表示,能得到两个非光滑边界
。
因此,自治方程的相空间可分为三个子空间:
,
,
。伴随两个非光滑边界
。如果变量x穿过
,这个系统的非光滑分岔将会出现,这对导出非线性系统的定性性质起到了有效作用。
3. 平衡点及其稳定性
自治系统相空间的三个子空间的平衡点可以作如下描述:子空间I中没有平衡点,子空间II的平衡点为
,子空间III的平衡点为
。
下面分别由雅可比矩阵对应的特征值来确定其每个子空间的稳定性。
对于
,其雅可比矩阵
在平衡点处为
, (4)
则其特征多项式为
。 (5)
在平衡态的特征值为下式
。 (6)
我们可以推导出有关
的稳定性条件,在
处当
且
,则平衡点
为
稳定焦点,若
,平衡点
为鞍点。在这个系统中,齿轮允许自振荡的固有频率为
,这意味着在的两个子空间
,齿轮系统的轨道具有相同的频率。而由于
是无量纲阻尼,则
总是大于0,所以不会发生Hopf分岔。当
其相应的特征值超过零点时,平衡点变得不稳定,可能会发生fold分岔。
4. 非传统的分岔分析
切换不连续点附近的非光滑动力学的演化可以用广义雅可比矩阵
来研究,该矩阵表示为如下形式:
,
。 (7)
当
中,
不存在,所以
,
。其雅可比矩阵
在这个平衡状态如下式:
, (8)
其特征多项式为
。 (9)
在平衡态的特征值为下式
。 (10)
在方程(10)中可以得出,不连续边界将不会出现Hopf分岔,当
会满足fold分岔的条件。
5. 齿轮系统的方程描述数值模拟
5.1. 无量纲一齿侧间隙一半的影响
本文采用两段式参数设置,对不同参数的齿轮传动系统进行了分析。
i):
,
,
。
ii):
,
,
。
在这一节中,我们分别考虑了一齿侧间隙的一半、啮合刚度和频率对两个不同参数下系统的影响。首先,根据(i)的参数,得到系统在无量纲一齿侧间隙影响下的分岔图和李雅普诺夫指数图,如图2(a),图2(b)所示。在分岔图中,我们可以看到系统一直在混沌状态。为了进一步验证它,我们可以根据李雅普诺夫指数图进一步观察,可以看到,LE1总是大于零的,可以看出在这个系统中齿侧间隙的一半总是处于混沌状态,所以我们可以说一齿侧间隙的一半对系统没有影响。此外,根据系统在随机的两个一齿侧间隙的一半b下进行数值模拟,得到其poincaré映射图,从图2(c),图2(d)中,我们可以进一步得出图特征总体是相似的。
 (a)
(a) 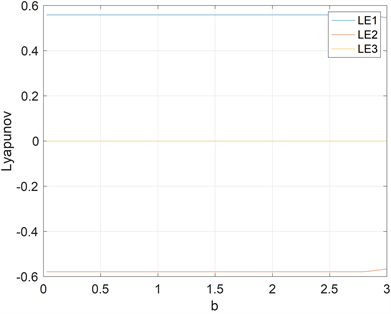 (b)
(b)  (c)
(c) (d)
(d)
Figure 2. The diagrams of (a) Bifurcation, (b) Lyapunov exponents, (c) Poincaré mapping of
and (d) Poincaré mapping of
for system (1) in parameter (i) and
图2. 系统(1)在参数(i)以及
下的(a) 分岔图,(b) 李雅普诺夫指数图,(c)
下poincaré映射图以及(d)
下poincaré映射图
5.2. 无量纲啮合刚度的影响
首先,根据(ii)的参数,得到系统在无量纲啮合刚度影响下的分岔图和李雅普诺夫指数图,如图3(a),图3(b)所示。在分岔图中,我们可以看到系统在
时系统处于简单运动状态,
时系统处于复杂运动状态。为了进一步验证它,我们可以根据李雅普诺夫指数图进一步观察,可以看到,LE1并不总是大于零,总体而言,可以验证其在
时系统处于简单运动状态,
时系统处于复杂运动状态。此外,在不同的啮合刚度k下进行数值模拟,可以观察到在啮合刚度
时,系统处于简单运动状态。在啮合刚度
时,系统处于复杂运动状态。因此,我们可以得到啮合刚度对系统有影响。对比不同的参数,可以得到应该尽量减少啮合刚度,以减少齿轮系统的损坏。
 (a)
(a)  (b)
(b)  (c)
(c) (d)
(d)
Figure 3. The diagrams of (a) Bifurcation, (b) Lyapunov exponents, (c) Poincaré mapping of
and (d) Poincaré mapping of
for system (1) in parameter (i) and
图3. 系统(1)在参数(i)以及
下的(a) 分岔图,(b) 李雅普诺夫指数图,(c)
下poincaré映射图以及(d)
下poincaré映射图
5.3. 无量纲啮合频率的影响
首先,根据(ii)的参数,得到系统在无量纲啮合频率影响下的分岔图和李雅普诺夫指数图,如图4(a),图4(b)所示。在分岔图中,我们可以看到系统在随着
越大,系统的混沌状态会慢慢消失。为了进一步验证它,我们可以根据李雅普诺夫指数图进一步观察,可以看到,LE1并不总是大于零,总体而言,可以验证其在
系统处于简单运动状态,
时系统处于混沌状态。此外,在不同的啮合频率
下进行数值模拟,可以观察到在啮合频率
时,系统处于复杂运动状态。在啮合频率
时,系统处于简单运动状态。因此,我们可以得到啮合频率对系统有影响。对比不同的参数,可以得到应该尽量增加啮合频率,以减少齿轮系统的损坏。
 (a)
(a)  (b)
(b)  (c)
(c)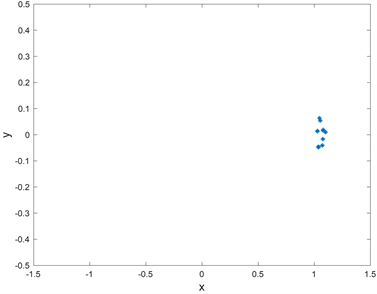 (d)
(d)
Figure 4. The diagrams of (a) Bifurcation, (b) Lyapunov exponents, (c) Poincaré mapping of
and (d) Poincaré mapping of
for system (1) in parameter (i) and
图4. 系统(1)在参数(i)以及
下的(a) 分岔图,(b) 李雅普诺夫指数图,(c)
下poincaré映射图以及(d)
下poincaré映射图
6. 簇发振荡及其机理分析
基于之前的稳定性及其分岔分析,因为激励频率远小于未扰动系统的固有频率,系统(1)将会穿过快变量x(或y)并表现出不同类型的簇发振荡。为了揭示扰动存在时系统的非光滑动力学,我们在这个部分将固定参数
。
图5为参数
,
,
,
,
下数值模拟的扰动现象,根据数值模拟,可以看到尖峰态和静息态在一个周期内交替出现。
 (a)
(a) (b)
(b)
Figure 5. Periodic bursting oscillation for
,
,
,
,
. (a) Phase portrait, (b) Time history
图5.
,
,
,
,
时的周期簇发振荡。(a) 相图,(b) 时间历程曲线图
另一种振荡模式为参数
,
,
,
,
如图6所示。从转换相图与平衡分支的叠加图6(d)中,我们可以解释周期振荡的机理,发现轨迹在周期簇发振荡中同时表现出SPs和QSs。轨迹在边界上滑动。当点
时,系统处于SPs,这个点总是向左滑动。当一个点到达非光滑边界(
)时,它突然跳到另一个分支并保持SPs,当这个点到达
时,系统完成了半个周期的簇发振荡运动。同样地,当点
向右滑动时,它会碰到一个非光滑的边界(
),然后突然跳到上面的分支,此时系统已经完成了一个完整的簇发振荡运动周期。这种簇发振荡机制我们称它为fold/fold簇发。
 (a)
(a)  (b)
(b)  (c)
(c)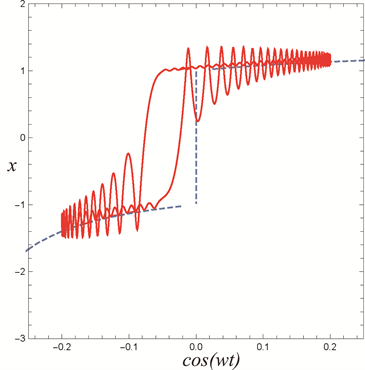 (d)
(d)
Figure 6. Periodic bursting oscillation for
,
,
,
,
. (a) Phase portrait, (b) Time history, (c) Poincaré mapping, (d) Overlap of the transformed phase portrait and equilibrium branches on the
图6.
,
,
,
,
时的周期簇发振荡。(a) 相图,(b) 时间历程曲线图,(c) Poincaré映射图,(d) 转换相图与平衡分支在
平面的叠加图
7. 结论
本文基于一类齿轮传动系统,应用快慢分析方法,将系统分为快子系统和慢子系统。通过平衡点的稳定性和分岔分析,得到了啮合刚度以及激励频率对齿轮传动系统有一定的影响,并通过分岔图以及李雅普诺夫指数的对比,选取了合适的参数结合其poincaré映射图,验证其准确性。
通过数值模拟表明,在工程应用上,应该适当的降低啮合刚度,将啮合刚度控制在区间
之间,在啮合刚度
时,系统处于简单运动状态;在啮合刚度
时,系统处于复杂运动状态。与此同时,应该适当的增加啮合频率,可以观察到在啮合频率
时,系统处于复杂运动状态;在啮合频率
时,系统处于简单运动状态。另外,在文章中我们探索出齿轮传动系统时受非光滑因素的影响会一种簇发振荡模式:fold/fold簇发。
基金项目
国家自然科学基金(12172333)和浙江省自然科学基金(LY20A020003)资助。
参考文献
NOTES
*通讯作者。