Chordal Ring图CR8k(1,3,9)的交叉数

doi:10.12677/AAM.2022.114170

期刊菜单

Chordal Ring图CR_8k(1,3,9)的交叉数
The Crossing Number of Chordal Ring Graphs CR_8k(1,3,9)

DOI: 10.12677/AAM.2022.114170, PDF, HTML, XML, 下载: 167 浏览: 243
作者: 刘新瑶：辽宁师范大学数学学院，辽宁大连
关键词: 交叉数；图；画法；Crossing Number； Graph； Drawing

摘要: 图的交叉数是图论中重要的一个分支，国内外诸多学者对图的交叉数这一问题进行广泛的关注和深入的研究。Garey和Johnson证明了确定图的交叉数问题是NP-完全问题，因此图的交叉数目问题仍然值得研究。但是由于探究和证明难度比较大，国内外对图的交叉数目问题的研究进展比较缓慢。至今为止，图的交叉数的研究成果集中在典型图类上，只得到了较少图族交叉数的精确值。本文主要采用数学归纳法和反证法研究了Chordal Ring图CR_8k(1,3,9)的交叉数。对于Chordal Ring图CR_8k(1,3,9)，给出一个交叉数为2k的好的画法，从而确定Chordal Ring图CR_8k(1,3,9)的上界。采用数学归纳法，以k=2时，cr(CR₁₆(1,3,9))=4为基础，假设k-1时，不等式cr(CR_8k(1,3,9))≥2(k-1)成立。采用反证法，将CR_8k(1,3,9)的边集分为不相交的2k组，讨论所有可能情形，证明了Chordal Ring图CR_8k(1,3,9)的下界。因此证明了：cr(CR8k(1,3,9))=2k(k≥2)。

Abstract: The crossing number of graphs is an important branch of graph theory. Many scholars at home and abroad have paid extensive attention to and studied the crossing number of graphs. Garey and Johnson proved that the problem of determining the number of intersects of graphs is NP-complete, so the problem of the number of intersects of graphs is still worth studying. However, due to the difficulty of exploration and proof, the research on the crossing number of graphs is slow at home and abroad. So far, the research results of graph crossing number focus on typical graph class, and only get the exact crossing numbers of very few families graphs. In this paper, a crossing number of chordal ring graphs CR_8k(1,3,9) are studied by mathematical induction and reduction. The upper bound of chordal ring graph CR_8k(1,3,9) is determined. By mathematical induction, on the basis of k=2, cr(CR₁₆(1,3,9))=4, and assuming k-1, the inequality is valid for cr(CR_8k(1,3,9))≥2(k-1). In this paper, the edge set of CR_8k(1,3,9) is divided into 2k groups with no intersection by the method of inverse proof, all possible cases are discussed, and the lower bound of CR_8k(1,3,9) of chordal ring graph is proved. It is thus proved that: cr(CR8k(1,3,9))=2k(k≥2) .

文章引用：刘新瑶. Chordal Ring图CR_8k(1,3,9)的交叉数[J]. 应用数学进展, 2022, 11(4): 1558-1566. https://doi.org/10.12677/AAM.2022.114170

1. 交叉数的研究进展

1.1. 六边形图

王晶等人 [1] 证明了六边形图的 $H_{3, n}$ 的交叉数，并给出了关于 $H_{m, n}$ 交叉数的猜想：

$c r (H_{m, n}) = (m - 2) n .$

历莹 [2] 的论文里证明了：

$c r (H_{4, 2}) = 2 n (n \geq 2) .$

1.2. Knödal图 $W_{3, n}$

邓成瑞 [3] 证明了Knödal图 $W_{3, n}$ 的交叉数为：

${\begin{cases} c r (W_{3, 8}) = 0; c r (W_{3, 10}) = 1; \\ c r (W_{3, n}) = ⌊ \frac{n}{6} ⌋ + \frac{n \mod 6}{2}, n \geq 12. \end{cases}$

1.3. Chordal Ring图 $C R_{n} (x, y, z)$

Javaid等人 [4] 证明了 $C R_{n} (1, 3, 5)$ 的交叉数：

${\begin{cases} c r (C R_{n} (1, 3, 5)) = 0, n \equiv 0 (\mod 4); \\ c r (C R_{n} (1, 3, 5)) = 1, n \equiv 2 (\mod 4) . \end{cases}$

郑文萍等人 [5] 证明了 $c r (C R_{10} (1, 3, 7)) = 1$ ， $c r (C R_{n} (1, 3, 7)) = ⌊ \frac{n}{6} ⌋ + (n \mod 6) / 2$ ( $n \geq 12$ 且n为偶数)。

Muhammad Imran等人 [6] 提出 $C R_{n} (1, 3, 9)$ 的上界( $n \geq 12$ 且n为偶数)：

$c r (C R_{n} (1, 3, 9)) \leq {\begin{cases} ⌊ \frac{n}{4} ⌋ + (n \mod 4), n \equiv 0, 6 (\mod 8); \\ \frac{n}{3} + 3, n \equiv 4 (\mod 8); \\ ⌈ \frac{n}{4} ⌉ + (n \mod 4), n \equiv 2 (\mod 8) . \end{cases}$

同时Muhammad Imran等人证明了 $c r (C R_{10} (1, 3, 9)) = 1$ ， $c r (C R_{12} (1, 3, 9)) = 2$ ， $c r (C R_{14} (1, 3, 9)) = 1$ ， $C R_{16} (1, 3, 9) = 4$ ， $c r (C R_{18} (1, 3, 9)) = 4$ ， $c r (C R_{20} (1, 3, 9)) = 4$ ， $c r (C R_{22} (1, 3, 9)) = 5$ ，给出了 $C R_{8 k} (1, 3, 9)$ 的好的画法，确定了其交叉数的下界， $c r (C R_{8 k} (1, 3, 9)) \leq 2 k$ ；证明了 $c r (C R_{8 k} (1, 3, 9)) = 2 k (k \geq 2)$ 。但是我们发现文献里 $C R_{8 k} (1, 3, 9)$ 的证明过程中少讨论一些情形，存在几处漏洞。因此本文证明 $c r (C R_{8 k} (1, 3, 9)) = 2 k (k \geq 2)$ 。

2. Chordal Ring图 $C R_{8 k} (1, 3, 9)$ 的交叉数

2.1. Chordal Ring图 $C R_{8 k} (1, 3, 9)$

为了便于书写，下文将Chordal Ring图 $C R_{8 k} (1, 3, 9)$ 记为 $G_{k}$ ， $G_{k}$ 的顶点集和边集为： $V (G_{k}) = V \cup U$ ，其中 $V = {v_{i / 2} : i \in ℤ_{8 k} 且 i 是偶数}$ ， $U = {v_{(i - 1) / 2} : i \in ℤ_{8 k} 且 i 是奇数}$ ，

$E (G_{k}) = \cup_{i = 0}^{4 k - 1} {v_{i} u_{i}, v_{i} u_{i + 1}, v_{i} u_{i + 4}} .$

将 $G_{k}$ 的边集合分成4k个互不相交的子集，对于 $0 \leq i \leq 4 k - 1$ ，令 $E_{i} = {v_{i} u_{i}, v_{i} u_{i + 1}, v_{i} u_{i + 4}}$ 。如果本文不特别指出，每个顶点的下标模8k。对于 $0 \leq i \leq 4 k - 1$ ，每个 $E_{i}$ 都是 $E (G_{k})$ 的一部分，那么可以得到 $E (G_{k}) = \cup_{i = 0}^{4 k - 1} E_{i}$ ， $E_{i} \cap E_{j} = \emptyset$ ，其中 $0 \leq i \neq j \leq 4 k - 1$ 。令D是 $G_{k}$ 的一个好的画法，用 $f_{D} (E_{i})$ ( $0 \leq i \leq 4 k - 1$ )表示计算在画法D下与 $E_{i}$ 相关的交叉点数目的函数，

$f_{D} (E_{i}) = c r (E_{i}, E (G_{k}) - E_{i}) / 2$

$c r (D) = \sum_{i = 0}^{4 k - 1} f_{D} (E_{i}) .$

对于 $G_{k}$ 的一个好的画法D，记 $l_{i}^{D}$ 是满足 $\sum_{j = 0}^{l_{i} - 1} f_{D} (E_{i + j}) \geq 0.5 l_{i}$ 的最小正整数，其中 $0 \leq i \leq 4 k - 1$ 。当 $i \leq j$ 时， $H_{i, j} = \cup_{k = 1}^{j} E_{k}$ ， $0 \leq i \leq 4 k - 1$ 。

令 $C_{i} = v_{i} u_{i + 1} v_{i + 1} u_{i + 2} v_{i + 2} u_{i + 3} v_{i + 3} u_{i + 4} v_{i}$ ， $0 \leq i \leq 4 k - 1$ 。令 $B_{i} = \cup_{k = i}^{i + 3} {v_{k} u_{k + 1}}$ 。 $Q_{i} = u_{i} v_{i} u_{i + 1}$ ，设 $C_{i}$ 将平面分为 $i n t C_{i}$ 和 $e x t C_{i}$ 两个等价区域。

2.2. $G_{k}$ 交叉数的上界

引理2.1对于 $k \geq 2$ ， $c r (G_{k}) \leq 2 k$ 。

证明：如图1所示，给出了 $G_{k}$ 的一个只有2k个交叉数的好画法。

Figure 1. A good drawing of G_k

图1. G_k的一个好的画法

2.3. $G_{k}$ 交叉数的下界

2.3.1. $G_{2}$ 交叉数

引理2.2 $c r (G_{2}) = 4$ 。

证明：图 $G_{2}$ 与图 $H_{4, 2}$ 同构，如图2和图3所示，定义映射f如下， $f (v_{4}) = a_{0}$ ， $f (u_{4}) = a_{1}$ ， $f (v_{0}) = a_{2}$ ， $f (u_{0}) = a_{3}$ ， $f (u_{5}) = b_{0}$ ， $f (v_{1}) = b_{1}$ ， $f (u_{1}) = b_{2}$ ， $f (v_{5}) = b_{3}$ ， $f (v_{6}) = c_{0}$ ， $f (u_{2}) = c_{1}$ ， $f (v_{2}) = c_{2}$ ， $f (u_{6}) = c_{3}$ ， $f (u_{7}) = d_{0}$ ， $f (v_{3}) = d_{1}$ ， $f (u_{3}) = d_{2}$ ， $f (v_{7}) = d_{3}$ 。在历莹 [2] 的文章中，证明了 $c r (H_{4, 2}) = 4$ ，因此 $c r (G_{2}) = 4$ 。

Figure 2. A good drawing of G₂

图2. G₂的一个好的画法

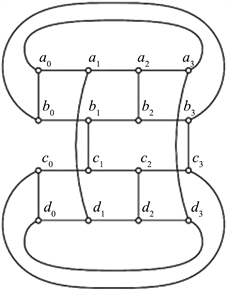
Figure 3. A good drawing of $H_{4, 2}$

图3. $H_{4, 2}$ 的一个好的画法

2.3.2. $G_{k}$ 交叉数的下界证明

引理2.3设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。则

$c r_{D} (B_{i}) + c r_{D} (B_{i}, E (G_{k}) - B_{i}) \leq 1$ ， $0 \leq i \leq 4 k - 1$ 。

证明：反证法。不失一般性，令 $c r_{D} (B_{0}) + c r_{D} (B_{0}, E (G_{k}) - B_{0}) \geq 2$ ，设在画法D中删掉 $B_{i}$ 得到画法 $D^{*}$ ，则 $c r (D^{*}) \leq c r (D) - 2$ 。由于 $D^{*}$ 是 $G_{k - 1}$ 的一个细分图的好的画法，由 $c r (G_{k - 1}) \geq 2 (k - 1)$ 得 $c r (D^{*}) \geq 2 (k - 1)$ ，所以有 $c r (D) \geq c r (D^{*}) + 2 \geq 2 k$ ，产生矛盾。因此 $c r_{D} (B_{i}) + c r_{D} (B_{i}, E (G_{k}) - B_{i}) \leq 1$ 得证。

引理2.4设C和C'是图 $G_{k}$ 中的两个圈， $P_{t}$ 是图 $G_{k}$ 中的一条以 $v_{1}$ 和 $v_{t}$ 为端点的路径，D是 $G_{k}$ 的一个好的画法，且 $V (C) \cap V (C^{'}) = \emptyset$ ， $V (C) \cap V (P_{t}) = \emptyset$ 。若C和C'相交，则 $c r_{D} (E (C), E (C^{'})) = 2 k$ ， $k \geq 1$ 。在画法D下，若 $P_{t}$ 与C相交，如果 $v_{1}$ 和 $v_{t}$ 位于 $D (C)$ 的同一区域，则 $c r_{D} (E (C), E (P_{t})) = 2 k$ ， $k \geq 1$ ；如果 $v_{1}$ 和 $v_{t}$ 位于 $D (C)$ 的不同区域，则 $c r_{D} (E (C), E (P_{t})) \geq 1$ 。

引理2.5设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (H_{i, i + 3}) = 1$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 在 $D (H_{i, i + 3})$ 的不同区域中，则 $l_{i}^{D} \leq 4$ ， $0 \leq i \leq 4 k - 1$ 。

证明：反证法。不失一般性，假设 $f_{D} (E_{0}) = 0$ ， $c r_{D} (H_{0, 3}) = 1$ ， $u_{0}, u_{5}, u_{6}, u_{7}$ 在 $D (H_{0, 3})$ 的不同区域，令 $Q = v_{4} u_{5} v_{5} u_{6} v_{6} u_{7} \cup P_{3} (u_{7}, v_{4 k - 1}) \cup v_{4 k - 1} u_{0} \cup P_{4} (v_{4}, u_{0})$ 。 $V (Q) \cap V (H_{0, 3}) = {u_{0}, u_{5}, u_{6}, u_{7}}$ ， $E (Q) \cap E (H_{0, 3}) = \emptyset$ ，由引理2.4知， $c r_{D} (E (Q), E (H_{0, 3})) \geq 2$ ，且 $c r_{D} (H_{0, 3}) = 1$ ，因此 $l_{0}^{D} \leq 4$ 。

引理2.6设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (E_{i + 1}, E_{i + 2}) = 1$ ，则 $l_{i}^{D} \leq 5$ ， $0 \leq i \leq 4 k - 1$ 。

证明：反证法。不失一般性，假设 $f_{D} (E_{0}) = 0$ ， $c r_{D} (E_{1}, E_{2}) = 1$ ， $l_{0}^{D} > 5$ 。由引理2.5知，同构意义下 $D (H_{0, 3})$ 只存在八种可能的画法，如图4所示。

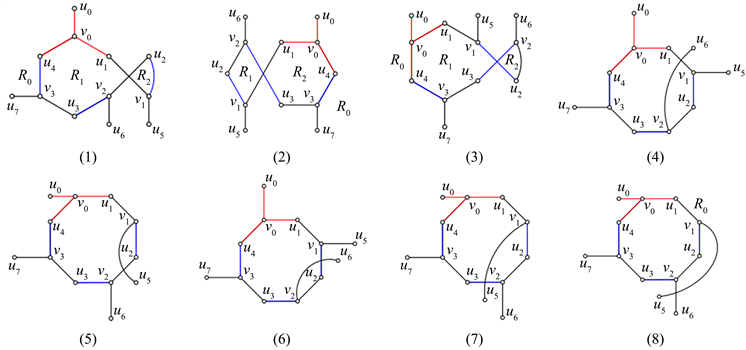
Figure 4. $c r_{D} (E_{1}, E_{2}) = 1$

图4. $c r_{D} (E_{1}, E_{2}) = 1$

引理2.7设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (E_{i + 2}, E_{i + 3}) = 1$ ，则 $l_{i}^{D} \leq 8$ ， $0 \leq i \leq 4 k - 1$ 。

证明：反证法。不失一般性，假设 $f_{D} (E_{0}) = 0$ ， $c r_{D} (E_{2}, E_{3}) = 1$ ， $l_{0}^{D} > 8$ 。由引理2.5知，同构意义下 $D (H_{0, 3})$ 只存在八种可能的画法，如图5所示。

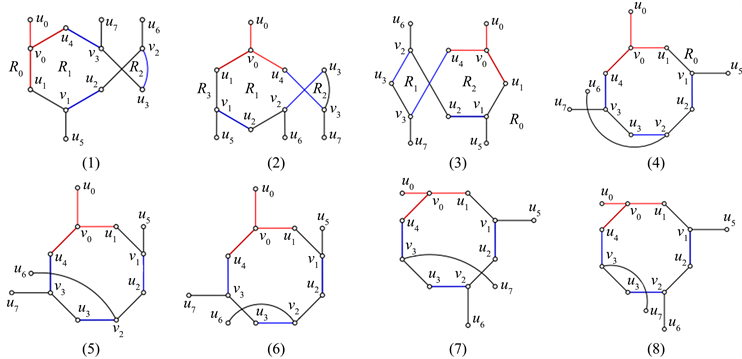
Figure 5. $c r_{D} (E_{2}, E_{3}) = 1$

图5. $c r_{D} (E_{2}, E_{3}) = 1$

引理2.8设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (E_{i + 1}, E_{i + 3}) = 1$ ，则 $l_{i}^{D} \leq 12$ ， $0 \leq i \leq 4 k - 1$ 。

证明：反证法。不失一般性，假设 $f_{D} (E_{0}) = 0$ ， $c r_{D} (E_{1}, E_{3}) = 1$ ， $l_{0}^{D} > 12$ 。由引理2.5知，同构意义下 $D (H_{0, 3})$ 只存在八种可能的画法，如图6所示。

Figure 6. $c r_{D} (E_{1}, E_{3}) = 1$

图6. $c r_{D} (E_{1}, E_{3}) = 1$

引理2.9设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (H_{i, i + 3}) = 0$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 两点在 $i n t C_{i}$ ，两点在 $e x t C_{i}$ ，则 $l_{i}^{D} \leq 5$ ， $0 \leq i \leq 4 k - 1$ 。

证明：反证法。不失一般性，假设 $f_{D} (E_{0}) = 0$ ， $c r_{D} (H_{0, 3}) = 0$ ， $l_{0}^{D} > 5$ 。且 $u_{0}, u_{5}, u_{6}, u_{7}$ 两点在 $i n t C_{0}$ ，两点在 $e x t C_{0}$ ，同构意义下 $D (H_{0, 3})$ 只存在三种可能的画法，如图7所示。

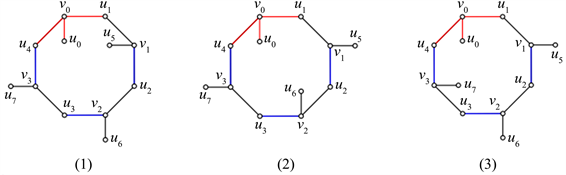
Figure 7. $u_{0}, u_{5}, u_{6}, u_{7}$ two vertices $i n t C_{0}$ two vertices $e x t C_{0}$

图7. $u_{0}, u_{5}, u_{6}, u_{7}$ 两点在 $i n t C_{0}$ 两点在 $e x t C_{0}$

引理2.10设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ ，若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (H_{i, i + 3}) = 0$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 一点在 $i n t C_{i}$ ，三点在 $e x t C_{i}$ ，则 $l_{i}^{D} \leq 12$ 。

证明：反证法。不失一般性，假设 $f_{D} (E_{0}) = 0$ ， $c r_{D} (H_{0, 3}) = 0$ ， $l_{0}^{D} > 12$ 。且 $u_{0}, u_{5}, u_{6}, u_{7}$ 一点在 $i n t C_{0}$ ，三点在 $e x t C_{0}$ ，同构意义下 $D (H_{0, 3})$ 只存在四种可能的画法，如图8所示。

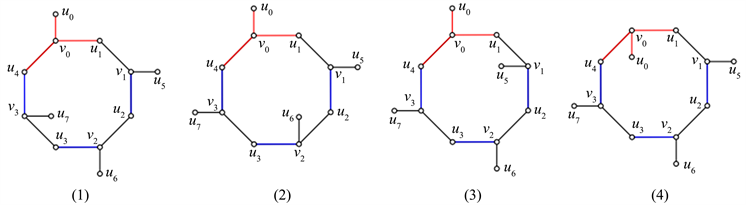
Figure 8. $u_{0}, u_{5}, u_{6}, u_{7}$ one vertice $i n t C_{0}$ three vertices $e x t C_{0}$

图8. $u_{0}, u_{5}, u_{6}, u_{7}$ 一点在 $i n t C_{0}$ 三点在 $e x t C_{0}$

引理2.11设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ ，若 $f_{D} (E_{i}) = 0$ ， $c r_{D} (H_{i, i + 3}) = 0$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 在 $e x t C_{i}$ ，则 $l_{i}^{D} \leq 12$ 。

引理2.12假设对于有序数对 $(i, j)$ ， $0 \leq i \neq j \leq 4 k - 1$ ，存在图 $G_{k}$ 的一个自同构映射 $\emptyset_{i, j}$ 满足 $\emptyset_{i, j} (E_{i + m}) = E_{j + m}$ ， $0 \leq m \leq 4 k - 1$ 。令D是图 $G_{k}$ 的一个好的画法，c是一个正常量。若对于 $0 \leq i \leq 4 k - 1$ ， $f_{D} (E_{i}) < c$ ，则存在一个正整数 $l (2 \leq l \leq 4 k)$ ， $\sum_{j = 0}^{l - 1} f_{D} (E_{i + j}) \geq l c$ ，则 $c r (D) \geq 4 c k$ 。

证明：若对于任意的 $i (0 \leq i \leq 4 k - 1)$ ，有 $f_{D} (E_{i}) \geq c$ ，则 $c r (D) \geq 4 c k$ 得证；

若存在 $i (0 \leq i \leq 4 k - 1)$ ，使得 $f_{D} (E_{i}) < c$ ，设 $n_{i}$ 是满足 $\sum_{j = 0}^{l - 1} f_{D} (E_{i + j}) \geq l c$ 中最小的l。令 $n_{i_{0}}$ 是所有 $n_{i}$ 中最大的数，若 $n_{i_{0}}$ 不唯一，则任选它们其中一个，不失一般性，假设 $i_{0} = 0$ 。按以下的规则将 $E_{i} (0 \leq i \leq 4 k - 1)$ 从 $E_{0}$ 开始升序排列：

1) 设 $E_{0}, E_{1}, \dots, E_{n_{0} - 1}$ 为第一组；

2) 令 $n_{0} = i$ ，则i是未分组子集 $E_{j}$ 中下标最小的数。若 $f_{D} (E_{i}) < c$ ，则 $E_{i}, E_{i + 1}, \dots, E_{i + n_{i} - 1}$ 为第二组。否则令 $E_{i}$ 自己为第二组；

3) 对于剩余未分组的 $E_{j}$ ，按照方法2)继续分组。当分组结束后，每个 $E_{i}$ 仅属于一个分组里。设M是 $f_{D} (E_{j}) < c$ 中最大的 $j (0 \leq j \leq 4 k - 1)$ 且 $g_{M}$ 为包含 $E_{M}$ 的分组。由 $n_{i_{0}}$ 的定义可知， $E_{0}$ 不在 $g_{M}$ 中(否则由规则2)得到 $n_{M} \geq n_{i_{0}}$ ，与 $n_{i_{0}}$ 的定义发生矛盾)。所以，每个 $E_{i}$ 仅属于一个分组。

通过上面的方式进行分组，每一组 $E_{i}$ 的平均交叉数至少是c，并且每个 $E_{i}$ 仅属于一个分组，因此 $c r (D) \geq 4 c k$ 得证。

定理2.13 设 $c r (G_{k - 1}) \geq 2 (k - 1)$ ，D是 $G_{k}$ 的一个好的画法， $c r (D) < 2 k$ ， $k \geq 3$ 。对任意一个 $i (0 \leq i < j \leq 4 k - 1)$ ，若 $f_{D} (E_{i}) < 0.5$ ，一定有以下四个结论之一：

a) $l_{i}^{D} \leq 4$ ；

b) $l_{i}^{D} \leq 5$ ；

c) $l_{i}^{D} \leq 8$ ；

d) $l_{i}^{D} \leq 12$ 。

证明：当 $f_{D} (E_{i}) < 0.5$ 时，若 $c r_{D} (H_{i, i + 3}) = 1$ ，由引理2.5，结论a成立；

若 $c r_{D} (E_{i + 1}, E_{i + 2}) = 1$ ， $c r_{D} (H_{i, i + 3}) = 0$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 两点在 $i n t C_{i}$ ，两点在 $e x t C_{i}$ ，由引理2.6和2.9，结论b成立；

若 $c r_{D} (E_{i + 2}, E_{i + 3}) = 1$ ，由引理2.7，结论c成立；

若 $c r_{D} (E_{i + 1}, E_{i + 3}) = 1$ 、 $c r_{D} (H_{i, i + 3}) = 0$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 一点在 $i n t C_{i}$ ，三点在 $e x t C_{i}$ 、 $c r_{D} (H_{i, i + 3}) = 0$ 且 $u_{i}, u_{i + 5}, u_{i + 6}, u_{i + 7}$ 在 $e x t C_{i}$ ，由引理2.8，引理2.10，引理2.11，可得结论d成立。

所以定理2.13得证。

定理2.14 $k \geq 2$ 时， $c r (G_{k}) \geq 2 k$ 。

证明：通过对k的归纳证明 $G_{k}$ 交叉数的下界。

当 $k = 2$ 时，由文献 [2] 知， $G_{2}$ 的交叉数是2；

假设 $k - 1 (k \geq 3)$ 时，不等式 $c r (G_{k - 1}) \geq 2 (k - 1)$ 成立，下证 $c r (G_{k}) \geq 2 k$ 。

假设 $c r (G_{k}) < 2 k$ ， $G_{k}$ 中的边集分为互不相交的4k组 $E_{i}$ ，对于任意序数对 $(i, j)$ ， $0 \leq i < j \leq 4 k - 1$ ，存在图 $G_{k}$ 的一个自同构映射 $\emptyset_{i, j}$ ，满足 $\emptyset_{i, j} (E_{i + m}) = E_{j + m}$ ，这里 $0 \leq m \leq 4 k - 1$ 。

情形1：若任意 $i (0 \leq i < j \leq 4 k - 1)$ ， $f_{D} (E_{i}) \geq 0.5$ ，则 $c r (G_{k}) = \sum_{i = 0}^{4 k - 1} f_{D} (E_{i}) \geq 2 k$ ，与假设矛盾，因此假设不成立， $c r (G_{k}) \geq 2 k$ ，定理得证。

情形2：若存在 $i (0 \leq i < j \leq 4 k - 1)$ ， $f_{D} (E_{i}) < 0.5$ ，可得定理2.13，再根据引理2.12，c取0.5，可得 $c r (G_{k}) \geq 2 k$ ，与假设矛盾，因此 $c r (G_{k}) \geq 2 k$ ，定理得证。

3. 结论

本文通过分支限界法证明Chordal Ring图 $C R_{8 k} (1, 3, 9) (k \geq 2)$ 的交叉数，给出相应图的好的画法，从而确定所研究图的上界。采用数学归纳法、反证法证明其交叉数的下界至少是2k，与假设矛盾，因此可以确定Chordal Ring图 $C R_{8 k} (1, 3, 9) (k \geq 2)$ 的交叉数是2k。即 $c r (C R_{8 k} (1, 3, 9)) = 2 k (k \geq 2)$ 。

参考文献

[1]	Wang, J., Ouyang, Z. and Huang, Y. (2019) The Crossing Number of the Hexagonal Graphs . Discussiones Mathematicae Graph Theory, 39, 547-554. https://doi.org/10.7151/dmgt.2092
[2]	历莹. 一类无限图的交叉数[D]: [硕士学位论文]. 大连: 辽宁师范大学, 2020.
[3]	邓成瑞.W_3,n和KmCn的交叉数[D]: [硕士学位论文]. 大连: 大连理工大学, 2006.
[4]	Javaid, I., Ismail, A., Salman, M., Ahmad, A. and Slamin, S. (2013) Labeling of Chordal Rings. Utilitas Mathematica, 90, 61-75.
[5]	Zheng, W., Lin, X., Yang, Y. and Deng, C. (2008) The Crossing Number of Knödal Graph . Utilitas Mathematica, 75, 211-224.
[6]	Imran, M., et al. (2015) The Crossing Number of Chordal Ring Networks. Periodica Mathematica Hungarica, 71, 193-209. https://doi.org/10.1007/s10998-015-0097-9

为你推荐

友情链接