1. 引言
作为平均震荡空间的推广(BMO),Q型空间在调和分析、偏微分方程以及位势理论中得到了广泛的研究,参见文献 [1] [2] [3]。Q型空间与BMO空间有类似的性质,在许多分析性问题的研究中,Q型空间可以是BMO空间很好的替代。最初,Essén等人将
推广到了欧几里得空间,参见文献 [4]。在2004年,Dafni和Xiao在文献 [5] 中利用一种新型的帐篷空间解决了分数阶Carleson测度和
空间的几个对偶问题,定义了
的对偶为包含Hardy空间
的分布空间并证明了一个原子分解。关于Q型空间更多的内容以及研究进展,可以参见文献 [6] [7] [8]。
基于类似的想法,作为BMO型空间在
上的推广,在文献 [9] 中,王春杰将Q型空间推广到
中,引入了
空间,通过利用Poisson积分给出了Carleson测度刻画。接下来,我们重述一下文献[9]中
的概念。
定义1.1令
,
包含了
上的所有可测函数f,则f满足
其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I。
董建锋将
的概念推广到
型群上,记为
,参见文献 [10]。在2016年,Zhao在文献 [11] 中引入了
上的Hardy-Hausdorff空间,得到了Hardy-Hausdorff空间的原子分解,证明了 Hardy-Hausdorff空间与
空间的对偶性。
通过定义1.1我们可以看出,空间
与幂函数
有关。一个很自然的问题就是
中的幂函数
是否可以用一个单调递增的权函数替代。因此,我们引入和研究了Heisenberg群上一个更为普遍的空间
,为了方便,本文研究
的相关问题,对于高维形式
的研究可类似,二者均可视为
的推广。
定义1.2设K是
上的增函数。若
满足
则称
。其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I并且该式的上确界取遍
中所有的方体I。
本文的主要目的是研究
上的Q型空间
。本文主要包括如下内容:在第二部分,介绍了相关的概念,研究了
的性质,给出了
与BMO空间的关系;在第三部分,利用辅助函数给出了
的Carleson测度刻画。
在本文中,如果存在一个正的常数C满足
,可写作
。另外,如果 和
和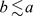 都成立,可写作
都成立,可写作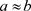 。我们假设
是单调递增的并且满足
。如下是我们将会用到的几个函数空间:
。我们假设
是单调递增的并且满足
。如下是我们将会用到的几个函数空间:

2. 的基本性质
的基本性质
在复空间
中,Siegel上半空间
被定义为
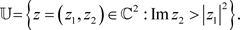
集合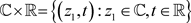 构成了Heisenberg群
,其中
。如果
,那么
构成了Heisenberg群
,其中
。如果
,那么
且
,其中
。
和
可以通过在原点进行如下的映射等同起来:
令
,f的梯度及其梯度的长度分别为
和
其中
并且
。在
中,
被称为函数f与g的卷积。
为了研究
的性质,我们需要如下辅助函数:
并且在全文中假设辅助函数
满足如下两个条件:
(1)
(2)
对于任意的方体
,
是I的中心,则基于I的Carleson盒子定义为
定义2.1令
。如果存在常数
满足
称
上的正Borel测度
为p-Carleson测度。
定理2.2
当且仅当
其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I。
证明根据定义1.2,利用变量替换:
,我们可以得到
定义2.3令
且
。若f满足
那么,称
。其中I是
上的一个区间,
是区间I的长度,并且该式的上确界取遍
中所有的方体I。
下面我们给出空间
与
之间的关系。
定理2.4
(1)
;
(2) 若
,则
。
证明(1)假设
并且m表示Lebesgue测度。那么对于任意方体I以及
,我们有
由于K是非减函数,于是
注意到
那么
于是
即
。
(2) 若
成立。设I为一个方体,
并满足
。则
并且
由于
我们可以得到
因此
,根据(1)知
。
3. Carleson测度刻画
为了研究
的Carleson测度刻画,我们需要文献如下的Hardy型不等式,参见文献 [12]。
引理3.1令
并且
。假设
和
在区间
上是非负可测的。如果对于所有非负可测函数f,
(1)
成立,当且仅当
(2)
成立,当且仅当
在
上,用
定义Schwarz函数族。接下来我们证明与权函数有关的Stegenga型不等式。
引理3.2假设K满足
和
令
并且
满足
。那么对于任意的以
为中心的方体I和J且
,存在与
和J无关的常数
使得
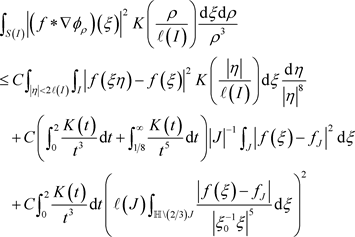
成立,其中
并且
。
证明由于
,
首先令
并且函数
满足,当
时,
,
并且
。记
,其中
且
。
是一个常数并且
表明
。因为
,
令
是
上以原点为中心的单位圆柱。设
并且
。于是
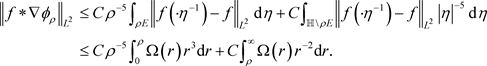
利用引理3.1,得
因此,对于
,记
其中
由于
从而
且
所以
接下来考虑
。注意到
于是
用与
相同的方法,可以得到
对于
,由于
,

如果
并且 ,则有
。因此
,则有
。因此
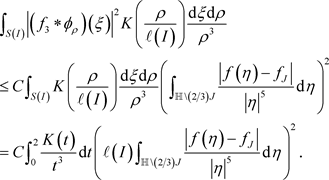
综合以上不等式,可得所证。
定理3.3假设K满足(2),
满足
。令
且
,则
当且仅当存在一个常数
满足
(3)
证明
表示
并且
。首先,若
。由定理2.4,我们可以得到
且
。令I与J是
上以原点为中心的方体,满足
,则
。那么
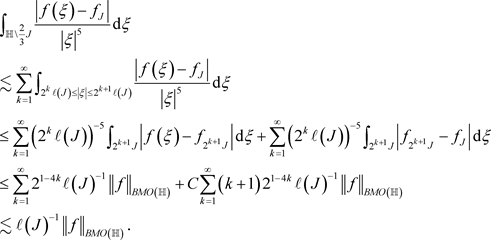
通过引理3.2我们可以推出
反过来,若(3)成立。要证
,只需证
记
,其中
,
,并且
。由于
那么对于
,利用Minkowski不等式,
结合引理3.1,可以推出
又因为
对于任意满足
的
,有
对于
,易得
并且由Minkowski不等式
所以
因此通过对
和
的估计,
即
。
致谢
作者衷心感谢李澎涛教授的指导与建议。
基金项目
山东省自然科学基金(项目编号:ZR2020MA004);国家自然科学基金(项目编号:11871293)。