基于对偶变量的计算机代数证明的机器检验

Machine Checking for Computer Algebraic Proofs Based on Dual Variables

摘要: 代数推理是目前验证门级整数乘法器最有效的方法之一。实用代数演算是一种涵盖了代数推理并能进行有效证明检验的证明格式。尤其是在代数编码中添加对偶变量生成统一的PAC证明。因为PAC证明文件非常大，且验证过程可能包含错误，本文介绍了一种验证检验器PACHECK2，通过对PAC证明格式进行修改，导出由一系列线性组合组成的证明。进一步识别异或门，分块进行线性组合，减少证明规则的使用，生成简洁的证明。实验表明新的检验器PACHECK2能有效检验证明，验证效率更高，同时提供详细的错误信息。为乘法器的验证提供了一个有效的检验器。

Abstract: Algebraic reasoning is one of the most effective methods to verify gate level integer multiplier at present. Practical algebraic calculus is a proof scheme that covers algebraic reasoning and can perform effective proof checking. In particular, adding dual variables to algebraic coding generates uniform PAC proofs. Because the PAC proof file is very large and the verification process may contain errors, this paper introduces a proof checker PACHECK2. By modifying the PAC proof format, a proof composed of a series of linear combinations is derived. To further identify XOR gates, the linear combination of blocks can reduce the use of proof rules and generate simple proof. The experimental results show that the new checker PACHECK2 can effectively check the proof, the verification efficiency is higher, and at the same time, provide detailed error information. It pro-vides an effective checker for the verification of the multiplier.

1. 引言

形式验证的目的是证明或否定给定系统相对于特定规范的正确性。但是，在计算机代数系统中验证过程也可能包含错误。为了增加验证结果的可信度，必须检验验证工具，一种常见的方法是生成证明证书，该证书包含验证过程中的所有步骤，且可以由一个独立的证明检验器进行检验。

许多形式验证的应用程序使用可满足性(SAT)求解，将验证问题建模为一个SAT问题，通过生成消解证明和子句证明 [1] 如DRUP [2] [3]、DRAT [4] 和LRAT [5]，来检验验证结果。甚至一年一度的SAT竞赛中，从2003年开始要求提供不可满足性证书，并提供不同的消解和子句证明格式。但是，该方法不可扩展，一些应用无法使用SAT求解，例如算术电路的形式验证，特别是乘法器电路的形式验证。

另一种方法是用计算机代数 [6] 验证门级乘法器，总体思路是将电路建模成一组多项式，然后进行Gröbner基 [7] 计算，通过对多项式进行约化，检验这些多项式是否隐含电路规范多项式。然而，当乘法器的末级加法器是生成和传播(GP)加法器时，很难用计算机代数来验证。在 [8] 中用简单行波进位(RC)加法器替换GP加法器，将SAT和计算机代数结合起来用于验证复杂门级乘法器。最近扩展了 [8] 的方法，在门级乘法器的多项式编码中表示负文字的对偶变量，在代数推理中考虑了对偶变量，和可以简化复杂末级加法器的新进位重写方法，还引入了尾部替换的概念。从而消除乘法器验证中对SAT求解器的调用。

为了验证代数推理结果的正确性，需要调用代数证明系统多项式演算(PC) [9]，PC作用于多项式，包含每个证明步骤的结论多项式，但缺少验证步骤的来源信息，无法有效检验验证结果。通过将从计算机代数系统中提取的证明转换为PC中的多项式反驳，从而将抽象的PC规则转化成具体的证明格式，称为实用代数演算(Practical Algebraic Calculus，简称PAC) [10]。PAC中存储代数推理验证过程中完整的证明步骤，检验过程中，要确保每一个证明步骤的正确性，并进一步检验至少一个结论多项式与目标多项式匹配，来检验验证结果的有效性。因此，也可以定位证明中错误的证明步骤。

在门级电路的多项式编码中添加了对偶变量，消除乘法器验证中的SAT求解器调用，并且能够提供统一的PAC证明。避免了两种不同的推理方法生成两种不同证明格式的证明证书DPUP和PAC [4]，导致在证明参数中存在漏洞。同时有些复杂乘法器，尤其是bp-wt-cl架构的乘法器，验证过程中使用大量的规则降低了检验的效率。

本文通过对工具teluma中获得的单个的、统一的PAC证明格式进行修改，导出一系列线性组合组成的证明。该证明格式更加简洁。本文中主要是展示新的检验器Pacheck2，可以有效检验各种复杂门级乘法器，并且可以找到证明中的错误，检验效率更高。

2. 基本概念

本节介绍算术电路验证，多项式方程的实用代数演算和对偶变量。

2.1. 算数电路验证

在本文中考虑门级无符号整数乘法器电路C，以与非图(AIG)的形式给出，具有2n个输入位 $a_0,\cdots ,a_{n-1},b_0,\cdots ,b_{n-1}$ 和2n个输出位 $s_0,\cdots ,s_{2n-1}$，其余内部节点由 $l_1,\cdots ,l_k$ 表示。设 $X=\left\{a_0,\cdots a_{n-1},b_0,\cdots ,b_{n-1},l_1,\cdots ,l_k,s_0,\cdots ,s_{2n-1}\right\}$。对于所有可能的输入 $a_i$， $b_i$，乘法器C是正确的当且仅当规范 $L=0$ 成立，其中

$L=-{\displaystyle \underset{i=0}{\overset{2n-1}{\sum }}{2}^i{s}_i}+\left({\displaystyle \underset{i=0}{\overset{n-1}{\sum }}{2}^i{a}_i}\right)\left({\displaystyle \underset{i=0}{\overset{n-1}{\sum }}{2}^i{b}_i}\right)$

定义1. 项 $\tau =x_1^{d_1}\cdots x_r^{d_r}$ 是变量幂的乘积，其中 $d_1,\cdots ,d_r\in {\rm N}$， $\left[X\right]$ 表示项的集合。单项式 $c\tau$ 是项的乘积，其中 $c\in R\backslash \left\{0\right\}$，多项式p是单项式的有限和。

定义2. (字典项序)将序 ≤ 固定在一组项上对所有项 $\tau$， ${\sigma }_1$， ${\sigma }_2$ 保持 $1\le \tau$ 和 ${\sigma }_1\le {\sigma }_2\Rightarrow \tau {\sigma }_1\le \tau {\sigma }_2$，如果对于所有的项 ${\sigma }_1=x_1^{d_1}\cdots x_r^{d_r}$， ${\sigma }_2=x_1^{e_1}\cdots x_r^{e_r}$，有 ${\sigma }_1<{\sigma }_2$，则令所有 $j<i$ 和 $d_i<e_i$，存在 $d_i=e_i$ 中的i索引，则这种顺序称为字典式项顺序。多项式 $p=c\tau +\cdots$ 中 $\tau$ (关于≤)称为前导项，记作 $\text{lt}\left(p\right)=\tau$。与前导系数 $\text{lc}\left(p\right)=c$ 构成前导单项式 $\text{lm}\left(p\right)=c\tau$。 $p-c\tau$ 叫作p的尾部。

在项集上，固定了一个字典项顺序，称为逆拓扑项顺序(RTTO)，这样门的输出变量总是大于输入变量。

定义3. 一组多项式 $I\subseteq Z\left[X\right]$ 称为理想，若 $\forall p,q\in I:p+q\in I$ 和 $\forall p\in Z\left[X\right]$ $\forall q\in I:pq\in I$。如果 $I=\left\{p_1{q}_1+\cdots +p_s{q}_s|q_1,\cdots ,q_s\in Z\left[X\right]\right\}$，则 $P=\left\{p_1,\cdots ,p_s\right\}\subseteq Z\left[X\right]$ 为I的基。则说I由P生成，写作 $I=\langle P\rangle$。

在 [5] 中，证明了L是否由C的门多项式和布尔值约束隐含的问题可以转换为理想成员问题来回答：“给定一个多项式 $q\in Z\left[X\right]$ 与多项式的(有限)集 $P\in Z\left[X\right]$，决定是否 $q\in \langle P\rangle$。”

定义4. C是一个电路，如果 $J\left(C\right)=\langle G\left(C\right)\cup B\left(X\right)\rangle \subseteq Z\left[X\right]$ 是由 $G\left(C\right)\cup B\left(X\right)$ 生成的理想，则电路C满足其规范当且仅当 $L\in J\left(C\right)$ [5]。

更一般的可以使用D-Gröbner基 [11] 理论。然后应用多元多项式约化并检验唯一最终结果是否为零来确定 $J\left(C\right)$。多项式集 $G\left(C\right)\cup B\left(X\right)$ 对于 $J\left(C\right)\subseteq Z\left[X\right]$ 的RTTO，自动产生D-Gröbner基 [5]，因此可以通过用这些多项式减少L来验证电路的正确性。 $B\left(X\right)$ 的约化通常通过立即约化大于1的指数来隐式处理，以加快计算速度。

2.2. 实用代数演算

下面我们介绍PAC中用到的一些代数概念 [12]。设X为变量集 $\left\{x_1,\cdots ,x_n\right\}$， $G\subseteq Z\left[X\right]$ 和 $f\in Z\left[X\right]$。

定义5. 若多项式集G的任意一个公共零点都是多项式f的零点，则称G蕴含f，记作： $G|=f$。也就是说： $G|=f\iff \forall u\in Z^n:\forall g\in G:g\left(u\right)=0\Rightarrow f\left(u\right)=0$

代数证明系统通常对多项式方程进行推理。给定 $G\subseteq Z\left[X\right]$ 和 $f\in Z\left[X\right]$，目的是证明每个 $g\in G\left(C\right)\cup B\left(X\right)$ 的约束 $g=0$ 隐含了方程 $f=0$。这意味着多项式 $g\in G$ 的每个公共布尔根也是f的根。在代数项中，f属于 $G\cup B\left(X\right)$ 生成的理想。

定义6. 让 $G\subseteq Z\left[X\right]$ 是一组有限的多项式。多项式 $f\in Z\left[X\right]$ 可以从G中推导出来如果 $f\in \langle G\rangle$，记作 $G|\text{}-f$。

验证证书，如PAC [9] 中的证书，允许监控验证过程。这些证明可以作为推理方法的副产品生成。PAC证明由三部分组成：1) 多项式的约束集，2) 核心证明，即模拟理想属性的证明步骤序列P，以及3) 目标多项式f。

PAC的核心使用两个证明规则：ADD和MULT。

$\begin{array}{l}\left[\text{ADD}\left(i,j,k,p\right)\right]\left(X,P\right)\Rightarrow \left(X,P\left(i\mapsto p\right)\right)\\ \text{provided}\text{that}P\left(j\right)\ne \perp ,P\left(k\right)\ne \perp ,P\left(i\right)=\perp ,\\ p\in Z\left[X\right]/\langle B\left(X\right)\rangle ,\text{and}p=P\left(j\right)+P\left(k\right)\mathrm{mod}\langle B\left(X\right)\rangle .\end{array}$

$\begin{array}{l}\left[\text{MULT}\left(i,j,q,p\right)\right]\left(X,P\right)\Rightarrow \left(X,P\left(i\mapsto p\right)\right)\\ \text{provided}\text{that}P\left(j\right)\ne \perp ,P\left(i\right)=\perp ,p,q\in Z\left(X\right)/\langle B\left(X\right)\rangle ,\\ \text{and}p=q\cdot P\left(j\right)\mathrm{mod}\langle B\left(X\right)\rangle .\end{array}$

这些规则对理想的加法和乘法性质进行建模，例如，在加法规则中，提供了三个多项式p、q、r，使得 $p+q=r$，以及p和q要么包含在S中，要么在早期的证明步骤中推导。因为 $p,q\in \langle S\rangle$，所以 $r\in \langle S\rangle$。 $Z\left[X\right]$ 上的PAC证明可以由证明检验器PACHECK和PASTEQUE [13] 进行检验。

通过添加删除和扩展规则来扩展我们最初的证明规则。在删除规则中，我们从P中删除那些后续步骤中不再需要的多项式，以减少工具的内存使用。引入一个扩展规则，它允许在知识库中添加更多的多项式和新变量，同时在原始变量集X上保留原始模型。

$\begin{array}{l}\left[\text{DELETE}\left(i\right)\right]\left(X,P\right)\Rightarrow \left(X,P\left(i\mapsto \perp \right)\right)\\ \left[\text{EXT}\left(i,v,p\right)\right]\left(X,P\right)\Rightarrow \left(X\cup \left\{v\right\},P\left(i\mapsto -v+p\right)\right)\\ \text{provided}\text{that}P\left(i\right)=\perp \text{and}v\notin X\text{and}\\ p\in Z\left[X\right]/\langle B\left(X\right)\rangle ,\text{and}{p}^2-p\equiv 0\mathrm{mod}\langle B\left(X\right)\rangle .\end{array}$

考虑下面的PAC证明。文件包含给定的多项式集合，PAC规则包含在文件 中。下面是PAC证明格式。

$\begin{array}{l}\langle \text{input}\rangle \langle \text{proof}\rangle \\ 1x-y;3\ast 1,z,xz-yz;\\ 2xz+yz+z;4+3,2,xz+z;\end{array}$

2.3. 对偶变量

多项式中单项的个数对多项式运算(如加法或乘法)的性能有很大影响。对偶变量是用一个变量来表示另一个变量的求反，为逆变器提供简写符号。将对偶变量集成到电路多项式编码中，引入单独的变量进行门变量的求反，这样，一个多项式的非就可以用另一个单项式来表示，减少多项式的使用。

如下所示，对于一个内部门变量 $l_i$， $1\le i\le k$，引入对偶变量 $dual\left(l_i\right)=f_i$。对偶变量用于AIG节点的多项式表示，以编码否定，例如，用多项式 $-l_3+f_1{f}_2$ 编码图1中的门 $l_3=\neg l_1\wedge \neg l_2$。

定义7. 设 $D\left(C\right)=\left\{-f_i-l_i+1|l_i是C的一个\text{AIG}内部节点,f_i=dual\left(l_i\right)\right\}\subseteq Z\left[X\right]$，设 $G_D\left(C\right)\subseteq Z\left[X\right]$ 是用对偶变量生成的门约束集。 $J_D\left(C\right)=\langle G_D\left(C\right)\cup B\left(X\right)\cup D\left(C\right)\rangle \subseteq Z\left[X\right]$， $G_D\left(C\right)\cup B\left(X\right)\cup D\left(C\right)\subseteq Z\left[X\right]$ 中的多项式根据RTTO排序，对于每个门变量 $l_i$，有 $f_i>l_i$，即表示逆变器门的对偶变量。

命题1. 令 $J_D\left(C\right)\subseteq Z\left[X\right]$ 如定义7所示。 $G_D\left(C\right)\cup B\left(X\right)\cup D\left(C\right)$ 是 $J_D\left(C\right)$ 的D-Gröbner基。

命题2. 对于所有布尔变量 $l_i$ 及其对偶表示 $dual\left(l_i\right)=f_i$， $f_i=1-l_i$，有 $l_i{f}_i=0$。

定义8. 设 $m_1$， $m_2$ 是 $m_1>m_2$ 的两个单项式，称 $m_1$ 和 $m_2$ 为对偶可合并当且仅当 $m_1=c{f}_i\tau$， $m_2=c{l}_i\tau$，c为常数， $\tau$ 为项，一些指数i。称单项式 $dmerge\left(m_1,m_2\right)=c\tau$ 为其对偶合并。

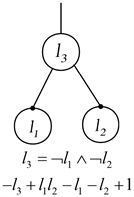
Figure 1. All polynomial encodings covered by AIG nodes

图1. AIG节点覆盖的所有多项式编码

Amulet 2.0 [14] 在PAC中生成证书。在下文中，将描述如何为新的进位重写技术生成证明步骤。首先，通过将对偶约束集 $D\left(C\right)$ 添加到证明的约束集，在PAC中包含对偶变量。也就是说，多项式的约束集是 $S=G_D\left(C\right)\cup D\left(C\right)$。 $B\left(X\right)$ 在PAC中被隐式处理。

在核心证明中，必须包括建模命题2的步骤。也就是说，每当多项式相乘时，都会生成一个乘法步骤，其中生成的多项式不会减少，并且可能包含 $c\in Z$， $f_i,l_i\in X$ 且 $\tau \in \left[X\right]$ 的 $c{f}_i\tau$ 形式的单项式。生成一个乘法步骤来计算 $\left(c{f}_i\tau \right)\left(-f_i-l_i+1\right)=-c{f}_i{l}_i\tau$。使用加法步骤可以取消 $-c{f}_i\tau$。以类似的方式对算法1执行的约化进行了处理。用 $q_l$ 乘以变量v的对偶约束，并将得到的多项式添加到p，以得到所需的约化。

例1令 $p=l_1{f}_2{f}_3+l_1{f}_2{l}_3+l_1{l}_2{f}_3+f_1{f}_2+l_2\in Z\left[l_1,l_2,l_3,f_1,f_2,f_3\right]$，用 $q_i$ 表示迭代i后的多项式q，并表示对偶合并。

$\begin{array}{l}{q}_0=l_1{f}_2{f}_3+l_1{f}_2{l}_3+l_1{l}_2{f}_3+f_1{f}_2+l_{2}r=0\\ q_1=l_1{l}_2{f}_3+f_1{f}_2+\boxed{l_1{f}_2}+l_{2}r=0\\ q_2=f_1{f}_2+l_1{f}_2+l_{2}r=l_1{l}_2{f}_3\\ q_3=\boxed{f_2}+l_{2}r=l_1{l}_2{f}_3\\ q_4=\boxed{1}r=l_1{l}_2{f}_3\\ q_5=0r=l_1{l}_2{f}_3+1\end{array}$

3. PAC检验器

3.1. PACHECK

Pacheck [13] 是PAC证明格式检验器Pactrim [9] 的扩展，由C语言实现的，可以有效地检验验证工具生成的PAC证明。Pacheck的默认模式支持PAC的扩展规则和索引。Pacheck还支持使用指数进行推理，但扩展规则仅支持布尔模型。

使用工具Amulet2.0验证乘法器，同时产生三个文件 ， 和 。其中 就是PAC证明证书，作为Amulet2.0的副产品获得。检验器Pacheck将这三个文件作为输入文件，具体检验过程就是理想成员问题：用 中包含的验证计算过程中的全部证明步骤验证 中的规范多项式是否包含在由 中的初始多项式生成的理想中。即用理想证明乘法器，若规范在理想中，则C为乘法器电路。

在Pacheck中，对变量进行排列支持顺序strcmp，−1 * strcmp，level，和−1 * level，在默认情况下，使用strcmp按字典顺序排列变量。另外一种排序方式是使用与给定证明文件中相同的变量顺序。多项式中的项使用与变量相同的顺序进行排序。为了减少证明文件的大小，引入索引来命名多项式，从而得到了一个更简洁的证明格式。

例2. 令 $\bar{x}\vee \bar{y}$ 和 $y\vee z$ 为两个子句，从中导出子项 $\bar{x}\vee z$。展示了如何在PAC中涵盖这种推导。

使用DeMorgan定律和可以用乘法表示逻辑“与”的事实，将这些子句转换为多项式方程。例如， $\bar{x}\vee \bar{y}=\top \iff x\wedge y=\perp$ 得出多项式方程 $xy=0$。翻译给定的子句，从而构建输入 和目标 。对于 中的PAC证明，引入了一个扩展变量 $f_z$，该变量对z的取反进行建模，即 $-f_z+1-z=0$。减少结论多项式的大小。并在PAC证明中显示删除规则。例如：

$\begin{array}{l}\langle \text{constraints}\rangle \\ 1x\ast y;\\ 2y\ast z-y-z+1;\\ \\ \\ \\ \langle \text{target}\rangle \\ -x\ast z+x;\\ \\ \\ \\ \end{array}$ $\begin{array}{l}\langle \text{proof}\rangle \\ 3=fz,-z+1;\\ 4\ast 3,y-1,-fz\ast y+fz-y\ast z+y+z-1;\\ 5+2,4,-fz\ast y+fz;\\ 2d;\\ 4d;\\ 6\ast 1,fz,fz\ast x\ast y;\\ 1d;\\ 7\ast 5,x,-fz\ast x\ast y+fz\ast x;\\ 8+6,7,fz\ast x;\\ 9\ast 3,x,-fz\ast x-x\ast z+x;\\ 10+8,9,-x\ast z+x;\end{array}$

3.2. PACHECK2

检验器Pacheck2是对Pacheck进行扩展得到的。Pacheck2多项式的内部表示与Pacheck几乎相同，都是输入由验证工具生成的三个文件 ， 和 ，同时结合了Pacheck的优点，支持扩展规则并能动态的检验中间证明步骤以定位错误。但是，Pacheck2只支持布尔模型，不再支持使用指数。

初始阶段中，对 的每个多项式进行排序并存储为推理。推理由给定的索引和多项式组成，并存储在哈希表中。检验过程中，动态应用证明检验分析 的每个步骤，用指针Token来识别证明中的组件，例如Token MINUS_TOKEN = “minus operator”，识别证明中的减法操作符；Token PERCENT_TOKEN = “linear combination operator”，识别证明中的线性组合运算。如果证明步骤是Add或Mult，则需要计算该步骤的结论多项式是否等于对先行多项式执行的算术运算。多项式的加法是通过以交错方式合并它们的单项式来执行的，多项式乘法将第一个多项式的每个单项式与第二个多项式的每个单项式相乘。并且对大于1的指数进行归一化。然后再解析并检验证明，检验加法或多步的结论多项式是否与 中的多项式匹配，以确定是否导出了规范的目标多项式。也就是说，解析一个证明步骤，并计算已知多项式的线性组合等于证明步骤的给定结论多项式。在Pacheck2中，支持删除推论，以减少内存使用。

4. 实验

本文中实验使用了一台带有Ubuntu18.04虚拟机的电脑，配备Intel(R) Pentium(R) CPU G4560 3.50 GHz和4 GB主内存。主内存限制为4 GB。时间以秒为单位，时间限制设置为300秒。本文使用工具Teluma生成证明证书，以验证输入位宽度为n的乘法器的正确性。因为Teluma工具去除了验证过程中对SAT求解器的需要，获得了单个的、统一的PAC证明格式。所以实验选用aoki基准，保证乘法器的FS加法器都是GP加法器。其中乘法器架构包括PPG：simple (sp)，Booth (bp)；PPA：array (ar)，Balanced delay tree (bd)，compressor tree (ct)，Wallace tree (wt)；FSA：carry look-ahead (cl)，Kogge-Stone (ks)，Ladner-Fisch-er (lf)，Brent-Kung (bk)。

Table 1. Proof checker contrast experiment

表1. 证明检验器对比实验

在实验中，选用了相同的实例。第一块显示了由Teluma直接生成的PAC证明 [15] 的证明生成(“gen”)和检验时间(“chk”)，以秒为单位。第二块显示了由Teluma生成的新PAC证明格式的证明和新的检验器Pacheck2。从表1中可以看出，检验过程中，Pacheck2比Pacheck效率要高，工具生成证明和Pacheck2检验证明所需的时间也更少。

5. 结论

本文对在代数编码中包含对偶变量并生成统一的PAC证明进行优化，使得该证明格式更加简洁。主要展示了检验器Pacheck2，能够有效的检验PAC校对。实验表明，新的检验器Pacheck2可以更高效的检验新扩展的各种乘法器，对复杂的bp-wt-cl架构的乘法器，在检验过程中效率也有很大提升。同时能定位证明步骤中的错误位置，提供详细的错误信息。在未来的工作中，希望在PAC中捕获更多通用的扩展规则，可以放宽条件 $p^2=p$。这个条件对于 $v^2=v$ 是必要的，但是可以取消，即使这意味着 $v^n$ 不能再简化为v，需要操纵指数。在未来工作中，我们希望能将对偶变量和尾部替换的一般技术应用于更一般的电路验证。

NOTES

^*通讯作者。