从问题提出的视角分析师范生的专门数学知识

Analyzing the Specialized Mathematical Knowledge of Normal School Students from the Perspective of Problem Posing

摘要: 问题提出是衡量师范生专门数学知识的一个标准。通过分析师范生基于勾股融方问题提出的与中学有关的数学问题，可了解师范生对中学数学知识掌握的程度以及问题提出的策略，以便为师范生的数学教学理论学习提供参考建议。

Abstract: Problem posing is a standard to measure the specialized mathematical knowledge of normal students. By analyzing the mathematical problems related to middle school raised by normal school students based on the Pythagorean integration problem, we can understand the degree of normal school students’ mastery of mathematical knowledge in middle school and the strategies proposed by the problem, so as to provide reference suggestions for normal school students’ learning of mathematical teaching theory.

1. 引言

数学教师的教学知识(Mathematical Knowledge for Teaching，简称MKT)自20世纪80年代起就受到数学教育工作者的重视，国内外已有许多关于数学教师教学知识的文献，其中鲍尔 [1] 把数学教师的教学知识(MKT)划分为六部分，由一般内容知识(CCK)、专门内容知识(SCK)、水平内容知识(HCK)、内容与学生知识(KCS)、内容与教学知识(KCT)、内容与课程知识(KCC)组成。除了一般内容知识，其他五类知识都与数学史有密切关系。“专门内容知识”是指教学所特有的数学知识和技能。对于许多“为什么”的回答，需要教师拥有专门化的知识，而数学史就是这样的专门化知识。Bair [2] 认为数学教师的专门内容知识(SCK)主要通过四种能力体现出来，这四种能力分别是：正确解答问题和证明推理的正确性的能力、能够使用多重表征的能力、能够识别并对概念相似的问题进行一般化的能力和问题提出的能力。问题提出能力是衡量数学教师SCK知识的一个指标。

早在20世纪上叶，问题提出已经开始受到心理学家的关注。80年代以后，众多学者开始研究并强调问题提出的教育价值 [3] [4]。爱因斯坦说过，提出一个问题比解决一个问题更重要。教师可以通过问题提出了解学生对数学的理解情况。数学家和数学教育家指出，问题提出是学生数学经验的重要组成部分。NCTM《学校数学课程与评价标准》提倡给学生更多机会提出自己的问题，指出，问题提出是“做数学”的核心活动。NCTM《数学教学专业标准》要求给学生机会从问题情境中提出问题，并通过改变给定问题中的条件，创设新的问题。但现阶段不论是小学还是中学，教师和学生的参考资料很多，教师选取现成的例题给学生讲解，学生用现成的习题进行练习巩固，长此以往就压抑了教师和学生提出问题的能力，其实提出问题是教师进行创作性的一种教学活动，提出问题需要深厚的知识功底。数学核心素养的六个部分都要求学生能在一定情境中提出问题，所以在教师教和学生学的过程中都要训练提出问题的能力，能不能提出好的数学问题对师范生来说很重要，为此，笔者对某师范大学大三学生的问题提出进行了测试，通过学生提出的问题来分析师范生的数学专门知识。

通过研究我们想得到以下问题的答案：以一个数学史问题作为任务背景，职前数学教师能运用哪些问题提出策略提出数学问题？在问题提出的评价水平上，职前教师的SCK知识表现如何？本文拟通过分析职前数学教师从一个给定的数学史料提出的问题来考察师范生提出问题的能力以及从问题提出这一个方面能否体现出职前教师所掌握的数学专门知识，以期能对职前教育有所启示。

2. 分析框架

2.1. 研究样本

本研究的样本是某师范大学数学专业大三共81位学生《数学文化与数学史》课程期末的一道测试题。该题是一道《九章算术》中勾股容方的数学史题。学生在勾股容方原问题的基础上，利用问题提出策略提出了与之相关的问题，通过对这些问题的分析来研究师范生的专门数学知识的体现。

先给出勾股容方题的原文：“今有勾五步，股十二步，问勾中容方几何。”首先让学生写出勾股容方公式，然后用刘徽的方法推导该公式，第3问要求学生根据“勾股容方”问题，编制有关均值不等式的问题。其中有68位学生提出了问题，部分同学给出了解答过程，13位学生没有提出问题。

2.2. 问题提出的策略

美国学者希尔佛(Silver)等人的研究表明，根据已知情境或已知问题提出新问题的具体策略有四种 [3] [4]：条件操作(改变已知条件)、目标操作(改变问题的目标)、对称性(将已知条件和目标互换)、链接(对现有问题进行扩充，新问题的解决依赖于已有问题的解决)。结合数学史融入数学教学的各种方式，我们将数学史问题提出的策略分成六种：再现式、自由式、情境式、条件式、目标式、对称式、链接式。

“再现式”策略就是直接采用数学史上“原汁原味”的问题，对应的数学史运用方式是复制式，即复制式数学史料本身是数学问题。“自由式”策略是根据一则数学史料(如历史上的数学史实、数学故事、数学问题、数学方法等)来提出数学问题，问题的条件和目标可根据需要自由选择。“情境式”策略是对历史上数学问题的情境进行改编，而保持已知条件和所求项不变。对历史上数学问题的条件和目标进行改编来提出新问题，分别称为“条件式”策略和“目标式”策略。同时改变问题情境和条件或目标的情形归入条件式或结论式。将历史上数学问题中的条件和目标进行互换，从而提出新的问题，这种策略称为“对称式”。将历史上数学问题的目标作为新的条件来提出问题，这种策略称为“链接式”，见表1。

Table 1. Examples of problem posing based on the history of mathematics

表1. 基于数学史的问题提出举例

问题提出的方式有改变情境、改变条件、改变目标、条件和目标互换及把原问题的目标作为条件提出问题的链接式 [5] 和条件与目标都改变的自由式六种策略。在这道题的基础上可以采用以上六种方式来提出问题，链接式的问题提出方式平时用得较少，但这道题的第2问已经求出了容方的边长，提出问题时可以把容方的边长作为已知条件用链接式提出新的问题。本课程的教师(作者之一)就是想通过该题考察职前数学教师在给定的数学史料和已知原题的结论基础上能否采用多种方式提出新的数学问题。要提出水平较高的问题必须善于通过联想把相关的知识点连接在一起，通过学生提出的问题可以了解学生掌握知识的广度和深度，学生提出的问题涉及的知识点多、广，说明他掌握的数学专门知识比较系统。

2.3. 水平划分

Bair [1] 提出了关于问题提出的5个评价指标如表2：

Table 2. Evaluation form of problem posing

表2. 问题提出的评价表

3. 学生的问题

3.1. 按问题提出策略对学生提出的问题进行划分

“勾股容方”问题的条件就是直角三角形的勾边和股边，目标是勾股容方的边长。根据“勾股容方”提出一道与均值不等式有关的问题是一道对提出问题的目标有限制条件的问题。提问题时可以把直角三角形中内接正方形的边长及均值不等式作为新的条件，目标可以是均值不等式或与均值不等式有关的其他关系。对学生提出的68道问题按照六类问题提出策略划分时采用的办法是：1) 符合策略要求的直接归入该类，如已知直角三角形的勾股和 $a+b$ 的值，求d的最大值，把原题中的条件和目标都进行了改变可归入自由式策略问题中；2) 提出的问题不能进行归类的，若有解答过程可参考解答过程进行归类，如用几何方法证明： ${\left(a+b\right)}^2\ge 2ab$，该题的解答过程是：因为三角形的内接正方形边长一定小于 $a,b$，

所以 $d=\frac{ab}{a+b}\le a,\frac{ab}{a+b}\le b$，所以 $\frac{2ab}{a+b}\le a+b,2ab\le {\left(a+b\right)}^2$。这个解答过程中是利用勾股容方的边长作

为已知结论利用的，从而可判断此策略为链接式；若没有解答过程就参考该生在第2问是否进行了解答以判断学生是否知道勾股容方边长的表达式进行归类，如 $S_{\Delta ABC}=S_{\Delta AED}+S_{\Delta DFB}+S_{正EF}$，当正方形EF面积最大时AD与BD的关系是什么？通过第2问的解答可知已求出内接正方形的边长可把该问题归入链接式。下图1是按问题提出策略对学生提出问题的频数图，见图1。

68道问题涉及的知识点有：两直角边和、积、容方边长、对角线、容方的周长、容方面积、斜边、三角形面积、均值等，见图2。

从图2可看出，学生提出的与容方的边长和边长的倍数有关的问题是与三角形两直角边的和、积、积的开方和容方的周长、对角线有关的问题，与容方的幂有关的问题只有容方的面积，与面积有关的问题涉及直角三角形的面积和容方的面积，与算术平均值有关的问题把几何、调和、反调和平均值都考虑

Figure 1. Frequency of problem posing based the students’ strategies

图1. 按问题提出策略对学生提出问题的频数

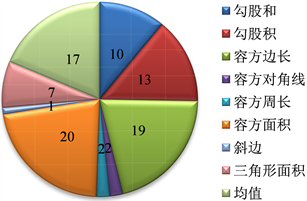
Figure 2. Distribution of knowledge points involved in students’ questions

图2. 学生提出问题涉及的知识点分布图

在内了。大部分问题的图形都是原问题的图形，有两个同学在提问题时改变了条件，一个是给出了半圆与直角三角形的图形，一个是取了斜边上的中点，比较三角形的中线和容方边长的关系，只有一位同学给出了地主给农民分土地的问题情境来提出问题。从以上分析发现，学生不敢变换图形或者通过增加条件提出问题与勾股容方相关的复杂问题。下面对不同的数学问题分别进行分析，其中 $S_{\Delta }$， $S_{四}$ 分别表示直角三角形的面积和三角形内接四边形的面积。

3.2. 自由式数学问题

自由式数学问题的信息见表3。

Table 3. Distribution of knowledge points in the list of free style questions

表3. 自由式问题一览表

3.3. 链接式数学问题

在数学问题中，链接式问题超过了一半以上，见表4。

Table 4. List of linked questions

表4. 链接式问题一览表

3.4. 目标式数学问题

目标式数学问题有：已知直角∆ABC，角A，B，C所对边分别为a，b，c，证明： $\frac{a+b}{2}\le \sqrt{ab}$。

4. 水平划分

按照Bair对问题提出的五种水平划分标准，自由式、链接式、结论式和情境式数学问题的划分标准如下所示：

目标式水平0：已知直角∆ABC，角A，B，C所对边分别为a，b，c，证明： $\frac{a+b}{2}\le \sqrt{ab}$

自由式水平0：已知有两个大小不定的正方形，其边长分别为a，b，问这两个正方形能够拼成两个长宽分别为a，b的长方形时，两个正方形边长应满足什么条件？

自由式水平1：若由直角三角形内正方形 $d=2$，求证： $ab>a+b$ ；

已知 $a+b=17$，求ab的最大值；

已知 $a+b=1$，求 $\frac{2}{a}+\frac{2}{b}$ 的大小；

互为勾股数形成三角形的三条边，则该三角形中包含的正方形边长不超过多少？

已知直角三角形的勾股和 $a+b$ 的值，求d的最大值；

自由式水平2：求直角三角形中矩形的最大面积为多少？

问a，b取何值时，有 $S_{四}$ 的面积最大？

a，b和固定下求最大面积的内切正方形。

问：直角三角形的勾股满足什么条件时，能使直角三角形的面积的 $\frac{1}{2}$ 等于直角三角形中的容方的面积？

设AB = a，BC = b，根据左面半圆图形利用知识证明均值不等式 $\sqrt{ab}\le \frac{a+b}{2}$ ；

问：直角三角形的勾股满足什么条件时，能使直角三角形的面积的 $\frac{1}{2}$ 等于直角三角形中的容方的面

积？

现有一直角三角形ABC，AC = b，BC = a，三角形内接的矩形CEDF，当矩形的边长满足什么条件时面积达到最大？

设一动点在AB上行动，问当D为哪个位置时，则正方形CEDF面积最大？

有一直角三角形土地，地主想把它的一部分分给农民，他说分的土地必须为一正方形，则农民应怎样划分才能使获得的土地最多？

现有一面倾斜的墙，为了不让墙倒下伤人，现决定架起保护措施，该保护措施为了使支持起同样大的空间用料最少，问该如何搭建？

自由式水平3：设有一长方形长为a，宽为b，令有一周长与其相同的正方形，试问二者谁的面积大？

自由式水平4：应用直角三角形边之间的关系证明 $DK<DH<DO<DE<DG$，即证

$\frac{2ab}{a+b}<\sqrt{ab}<\frac{a+b}{2}<\sqrt{\frac{a^2+b^2}{2}}<\frac{a^2+b^2}{a+b}$ ；

证明均值不等式链： $\frac{ab}{a+b}\le \sqrt{ab}\le \frac{a+b}{2}\le \sqrt{\frac{a^2+b^2}{2}}\le \frac{a^2+b^2}{a+b}$

链接式水平0：请用均值不等式的方法，判断勾股容方中d 与 $\frac{1}{4}ab$ 的大小；

求证： $ab\le a+b$ (a，b是任意正数)；

用几何方法证明： ${\left(a+b\right)}^2\ge 2ab$ ；

通过勾股容方判断，算术平均值 $\frac{a+b}{2}$ 和几何平均值 $\sqrt{ab}$ 哪个大？

用勾股容方问题证明均值不等式；

链接式水平1：判断并证明： $a+b$ 和 $\sqrt{ab}$ 的大小关系(a，b均为大于0的数)；

试用几何方法证明 $\frac{ab}{a+b}<\sqrt{\frac{ab}{2}}$ 这一不等式；

利用勾股容方的几何法证明： $ab\le \frac{{\left(a+b\right)}^2}{4}$ ；

$c=\frac{ab}{a+b}$，由此推出 $c^2\le \frac{ab}{2}$ ；

$\frac{1}{2}ab>{\left(\frac{ab}{a+b}\right)}^2$，求证该不等式；

证明 ${\left(\frac{ab}{a+b}\right)}^2\le ab$ ；

试证明： $\frac{2ab}{a+b}<\sqrt{ab}$ ；

判断 $\sqrt{ab}$ 与 $\frac{ab}{a+b}$ 的大小关系；

利用勾股容方问题求解 $\frac{a+b}{ab}$ 与 $\frac{a+b}{2}$ 的关系；

利用勾股容方，证明均值不等式 $\frac{2ab}{a+b}<\sqrt{ab}$ ；

已知直接三角形勾股分别为 $a,b$，且勾股容方的边长为d，试证明： $a+b\ge 2d$ ；

直角三角形内接正方形边长的两倍与勾和股的算术平均值之间有什么大小关系？

利用三角形内接正方形面积与三角形本身面积的关系，证明均值不等式 $\frac{2ab}{a+b}\le \sqrt{ab}$ ；

直角三角形直角边为 $a,b$ 内接正方形边长为 $\frac{ab}{a+b}$，探索 $\frac{ab}{a+b}$ 与 $\frac{a+b}{2}$ 大小关系；

已知勾股容方中的正方形边长为 $d=\frac{ab}{a+b}$，试证明 $\sqrt{ab}>\frac{2ab}{a+b}$ ；

证明任意以 $a,b$ 为直角边的RtΔ，内接正方形的边长都大于等于 $\frac{2}{\sqrt{ab}}$ ；

试证明任意直角三角形的面积一定不小于其内接正方形面积的两倍；

证明直角三角形内接正方形边长不大于直角三角形两直角边和的一半；

试比较Rt∆ABC内接正方形的边长与直角三角形直角边长和的一半的大小；

链接式水平2： $\frac{\sqrt{a^2+b^2}}{2}\ge \frac{ab}{a+b}$ ；

证明 $\frac{ab}{a+b}<\sqrt{\frac{a^2+b^2}{2}}$

$S_{\Delta }$ 与 $S_{四}$ 有什么关系；

请利用勾股容方的有关知识判断 $\frac{2ab}{a+b}$ 与 $\frac{a^2+b^2}{a+b}$ 的大小；

正方形边长的两倍 $\frac{2ab}{a+b}$ 和对角线的一半 $\frac{\sqrt{a^2+b^2}}{2}$ 哪个大？

取AB中点F，连接CF，利用均值不等式试证：ED < CF；

比较勾股容方的正方形边长的两倍和从 $a,b$ 为边的矩形周长的 $\frac{1}{4}$ ；

试证明勾股容方为直角三角形内部最大内接四边形； $S_{\Delta ABC}=S_{\Delta AED}+S_{\Delta DFB}+S_{正EF}$，当正方形EF面积最大时AD与BD的关系是什么？

直角∆ABC中各边长为d的正方形，问：边长为 $a,b$ 的长方形中最多能容下几个边长为d的正方形？

链接式水平3：比较 $d^2$ 与 $\frac{1}{4}ab$ 的大小；

比较 $\frac{ab}{a+b}$ 与 $\frac{\sqrt{ab}}{2},\frac{a+b}{4},\frac{a^2+b^2}{2\left(a+b\right)}$ 大小关系；

对比算术平均数与调和平均数的大小；

$a\le b$，证明： $S_{\Delta }\ge 2S_{四}$，并试推出一组均值不等式链；

已知直角三角形ABC，直角边长为a和b，CEDF为内接正方形，求证：正方形周长 $C\le a+b$ ；

$b\ge a$ 时有 $AD\ge DB$，可推出 $\sqrt{{\left(b-\frac{a+b}{ab}\right)}^2+{\left(\frac{a+b}{ab}\right)}^2}\ge \sqrt{{\left(\frac{a+b}{ab}\right)}^2+{\left(a-\frac{a+b}{ab}\right)}^2}$，当且仅当 $a=b$ 时等号成立；

链接式水平4：根据图形，在上面任意添加辅助线来比较：算术中项 $\frac{a+b}{2}$，几何中项 $\sqrt{ab}$，调和中项 $\frac{2}{\frac{1}{a}+\frac{1}{c}}$，反调和中项 $\frac{a^2+c^2}{a+c}$ 的大小；设 $A=\frac{a+b}{2}$， $B=\sqrt{ab}$， $D=\frac{2ab}{a+b}$， $E=\frac{a^2+b^2}{a+b}$，如何应用勾股

容方的方法比较A，B，D，E四个值的大小。

按照问题提出的指标68道问题的水平划分频数见表5。

Table 5. Frequency of problem posing level

表5. 问题提出水平划分频数表

从表5可看出具有水平1和水平2的同学人数最多，占69%，其次是具有水平1的同学，水平0的同学有10位，最少的是具有水平4的同学，只有4位，占6%。

问题提出策略用到了三种，通过链接式提出的问题有45个，占到了绝大多数，自由式提出的问题有22个，目标式只有1个，而条件式、情境式和对称式的问题都没有出现。

具有水平3的同学虽然提出的问题都不一样，但对原有问题都进行了扩展，问题的结构和背景都进行了改变，如求内接于直角三角形中矩形的最大面积；具有水平0的三位学生是直接给出了初中就已知的结果，如请证明： ${\left(a+b\right)}^2\ge 2ab$ 等，这类学生所掌握的有关直角三角形、内接长方形以及均值不等式的知识都很贫乏，所以提不出水平高级的问题；题目要求提出与均值不等式有关的问题，在水平1的同

学提出的问题是与算术平均数或几何平均值有关的问题，如判断 $\sqrt{ab}$ 与 $\frac{ab}{a+b}$ 的大小等；具有水平2的同学能变换勾股容方的边长与其它边的关系，如请证明 $\frac{ab}{a+b}<\sqrt{\frac{a^2+b^2}{2}}$ ；能够对原题涉及的知识点掌握

得好的同学能提出包含丰富联系的问题，如水平4的同学提出了问题：根据图形，在上面任意添加辅助

线来比较：算术中项 $\frac{a+b}{2}$，几何中项 $\sqrt{ab}$，调和中项 $\frac{2}{\frac{1}{a}+\frac{1}{b}}$，反调和中项 $\frac{a^2+b^2}{a+b}$ 的大小；设 $A=\frac{a+b}{2}$， $B=\sqrt{ab}$， $D=\frac{2ab}{a+b}$， $E=\frac{a^2+b^2}{a+b}$，如何应用勾股容方的方法比较 $A,B,C,D$ 四个值的大小。

对学生提出问题的水平分析

通过以上分析，具有水平4的学生只有4位同学，人数最少，这四位同学提出了有关均值不等式链的问题；其次是达到水平3的同学有7位，这7位学生能延伸容方的概念提出问题；能改变问题的结构提出问题达到水平2的同学人数最多。这说明学生对均值不等式的相关知识有一定的了解，可以和勾股容方问题、求最值问题联系起来，但能提出高水平问题的学生人数较少，没有把所学过的知识点与原问题建立起联系，这说明学生的专门数学知识是零散的，没有形成系统的知识网。

1) 提出问题水平低得原因：知识面较窄，不能把相关知识有机地建立起联系；

2) 反应了学生的真实水平：

3) 该问题的目标被限定是与均值不等式有关的问题，通过学生提出的问题可以了解学生理解的均值不等式是怎样的？有两位学生提出了有关均值不等式的链式不等式式不够的；

4) 对均值不等式的理解有以下几种情形：① 把均值不等式理解为基本不等式 $a^2+b^2\ge 2ab$

和 $\frac{2ab}{a+b}<\sqrt{ab}$ 的学生对均值不等式在理解上是有偏差的；② 与调和中项和反调和中项有关系的问题分

别有10个和4个；③ 学生通过自由式策略提出的均值不等式模型有创新，如把直角三角形改成了半圆模型；

5) 学生能够利用自由式、目标式和链接式三种策略提出问题，但没有条件式、情境式和对称式，其原因是题目要求根据勾股容方提出与均值不等式有关的问题，条件是直角三角形的勾、股边，目标是容方的边长，若改变条件必定改变目标，所以就没有条件式，有两位同学的问题中包含了情境，但条件与目标全都改变了，所以是自由式，对称式要求问题的条件和目标互换，但该题要求与均值不等式有关，所以对称式也不会出现。

6) 有3个问题是要求通过勾股容方来判断算术中项与几何中项的大小，但因题目没要求写出解答过程，所以看不出学生是否能真正通过勾股容方推导出均值不等式。

5. 错误分析

13位同学提出的无效问题是缺少条件和曲解公式的问题。缺少条件的问题如互为勾股数形成三角形的三条边，则该三角形中包含的正方形边长不超过多少？曲解公式的问题如已知直角∆ABC，角A，B，C

所对边分别为a，b，c，证明： $\frac{a+b}{2}\le \sqrt{ab}$。

6. 结论与启示

通过以上分析，我们得到如下结论：

1) 通过基于数学史的问题师范生可以提出不同水平的问题，能改变原问题的结构和背景提出概念相同问题的学生占大多数，不会提出问题或对原有问题不能做微小变化的同学的人数不多。

2) 衡量问题提出的指标有5个水平，从不同水平的体现可看出师范生对已学过知识的掌握情况，从而反应出师范生所掌握的专门数学知识。

3) 学生提出问题较弱的原因可能有：① 课上没讲；② 学生缺乏对符号语言与图形语言的转换能力；③ 均值不等式相关知识知道的少等。

4) 学生只能提出一些高中常见的不等式问题，但未见涉及函数等知识点的问题，高考不等式中的问题也未涉及。

提出问题是教师应该具有的教学能力，通过提出问题的水平高低可体现教师驾驭知识的能力和教学水平。所以在师范生的职前教育中应加强这方面的训练以丰富师范生的教学策略。通过数学史问题提出问题不仅可以锻炼学生提出问题的能力，而且可以丰富学生的数学文化素养。现在国内把数学史融入教学过程(HPM)的案例越来越多，渗入到了中小学及大学的课堂中，受到了师生的好评。但要将数学史融入课堂教学，数学史问题不可或缺。所以在师范生的培养过程中还要加强对问题提出策略的培养。

基金项目

广东省教育科研项目(高校)高等教育科学研究项目(2020GXJK395)；岭南师范学院高等教育教学研究合改革项目–“深度学习”背景下促进职前数学教师专业发展的研究合改革实践；广东省2021年度教育科学规划课题(教育综合改革专项)-SOLO分类法对高中数学学生学业质量水平评价的实践研究(2021JKZG086)。