考虑企业社会责任与回收质量的闭环供应链回收及定价决策

Recycling and Pricing Decision of Closed Loop Supply Chain Considering Corporate Social Responsibility and Recycling Quality

摘要: 本文构建了制造商主导并且进行企业社会责任投入的多级闭环供应链，在考虑废旧产品回收质量存在差异的基础上研究了集中决策、分散决策下不同回收模式对于废旧产品回收质量及供应链主体利润的影响。研究表明，制造商进行企业社会责任的投入有利于废旧产品回收质量的提升；无论在哪种回收模式下，随着制造商企业社会责任投入程度的不断增强，产品的零售价格会逐渐下降，从而有助于刺激市场需求，制造商的总利润、零售商的利润及系统的总利润均会有显著提升，但是会损害制造商自身的经济利润；从回收渠道选择角度考虑，制造商选择零售商回收模式效果最优。

Abstract: This paper constructs a multi-level closed-loop supply chain dominated by manufacturers and invested in corporate social responsibility (CSR), and studies the impact of different recycling modes on the recycling quality of waste products and the main profits of the supply chain under centralized decision-making and decentralized decision-making based on the consideration of the differences in the recycling quality of waste products. The research shows that the manufacturer’s CSR investment is conducive to improving the quality of waste product recycling. No matter in which recycling mode, with the increasing CSR input of manufacturers, the retail price of products will gradually decline, which will help stimulate market demand. The total profits of manufacturers, retailers and the total profits of the system will be significantly improved, but will damage the economic profits of manufacturers themselves with the increasing CSR input. From the perspective of recycling channel selection, it’s best for manufacturer to choose the retailer for recycling.

1. 引言

现代科技的高速发展及消费者的多样化需求使得产品更新迭代速度不断加快，与此同时产生的废旧产品给生态环境带来了不小的压力。随着政府对于循环经济的要求、公众对于环境友好型社会的向往、媒体对于企业不法行为的监督力度不断加强，不少企业选择通过逆向供应链“资源回收–再生产或处理”环节实现生产成本的降低及供应链可持续发展的双重目标，诸如IBM等大型制造商、苏宁等大型零售商纷纷投入闭环供应链的实践中。企业对废旧产品的回收在一定程度上体现了其承担企业社会责任(Corporate Social Responsibility，简称CSR)的决心。因此闭环供应链的实践可以在满足自身经济发展的同时赢得政府及社会各方的认可。

然而，废旧产品在回收的过程中由于消费者使用习惯及意识观念的不同存在很大的不确定性，回收质量参差不一给制造商的回收拆解再制造造成了一定的困难，回收率低也为制造商逆向供应链的推广实践带来压力。虽然政府可以通过补贴的形式鼓励回收商提升回收率，但是力度是有限的；且目前关于CSR与闭环供应链的研究中鲜有学者将废旧产品的回收质量与回收率都进行研究，因此如何从供应链发展的其他角度增强废旧产品的回收质量及回收率从而更有助于社会的可持续发展是值得研究的。本文在考虑CSR投入的闭环供应链中研究了废旧产品回收质量与供应链主体定价决策的相关问题。

2. 文献综述

闭环供应链中逆向供应链对于环境积极作用体现了企业愿意承担CSR中的环境责任。CSR作为一种高投资慢回馈的投资活动，虽然对于企业发展而言具有一定风险，但是Friedman等 [1] 认为，企业的CSR行为对提高自身及其利益相关者整体财务绩效具有积极的促进作用。Becker-Olsen等 [2] 从实证角度论述了企业CSR行为对消费者购买动机及行为的影响。由此可见，消费者在关注企业经济绩效的同时更关注企业承担的CSR对于社会起到的正向影响。

在现有的研究中，关于闭环供应链产品质量管理的研究分为回收过程产品质量控制及再制造过程产品质量控制等。在废旧产品的回收过程中，消费者使用时间或习惯的不同会导致产品出现不同程度的损耗，因此废旧产品回收质量差异会导致再制造环节成本有所不同。Savaskan R C、Atasu A、周雄伟等 [3] [4] [5] 学者将再制造成本刻画成关于废旧产品回收质量的一元线性函数，即废旧产品回收质量越高再制造成本越低；Xing K等 [6] 学者认为再制造成本与产品回收质量为指数关系。李舒玲 [7]、邹清明 [8] 等人考虑了回收质量水平符合正态分布的情形，研究表明回收率、销售量会随着回收质量的提高而增加。在再制造品质量控制过程中，其质量的高低将对其市场需求和闭环供应链各节点企业利润产生影响。刘家国 [9] 研究了新产品质量特征数大于再造品质量特征数时由于消费者偏好差异对供应链各节点企业利润的影响。Banindir等 [10] 学者考虑了单周期新产品和再制造产品之间存在单向替代的情况，研究发现当再制造品的单位产能需求较低时，即使它有单位成本优势，在产能紧张的情况下也很难盈利。Chen [11] 等基于废旧产品回收质量的不确定性，研究了消费者对于新产品和再制造产品的不同支付意愿及两阶段闭环供应链的动态决策问题。

以上研究均考虑了闭环供应链废旧产品回收过程中质量不确定的问题，但是鲜有学者对废旧产品的回收质量进行决策。然而在现实生活中，通过回收方的努力不仅可以提高废旧产品的回收率 [3] [4]，在一定程度上也可提升回收质量 [5]。例如零售商在销售电脑等3C产品时可与内胆包形成套餐价格进行出售，以此提醒消费者内胆包可以较好地保护产品以便回收时能够得到理想的回收价格。

在CSR与闭环供应链的相关研究中，学者就CSR投入主体及回收渠道的不同做了相应的研究。根据CSR投入主体可以分为制造商投入CSR、零售商投入CSR、制造商和零售商共同投入CSR(分摊)三种情况。Savaskan [3] 等将回收渠道分为制造商回收、零售商回收及第三方回收渠道，Liu等 [12] 则进一步研究了混合回收渠道竞争模型。由于处于渠道领导地位的主体具有更大的承担CSR的压力 [13]，所以本文构建了制造商主导并且进行CSR投入的多级闭环供应链模型，在考虑废旧产品回收质量存在差异的基础上研究了集中决策、分散决策下不同回收模式对于废旧产品回收质量及供应链主体利润的影响，并给出制造商进行CSR投入是时最佳回收渠道选择策略，弥补了CSR与闭环供应链关于废旧产品回收质量控制的相关研究。

3. 模型构建与求解

3.1. 问题描述与假设

本文考虑由一个制造商、一个零售商及一个第三方组成的多级闭环供应链，其中制造商为渠道的领导者，所有成员进行单周期完全信息下的Stackelberg博弈。

在正向供应链中，由制造商进行CSR的投入及负责新产品的生产；零售商决定产品的零售价格p。参照以往文献 [3] [6] 研究，本模型中需求函数为：

$q=\alpha -\beta p$ (1)

其中 $\alpha$ 表示市场容量， $\beta$ 表示消费者对产品的价格敏感系数， $\alpha >0,\beta >0$。本研究中假设消费者对于新产品和再制造产品之间没有明显的消费偏好，即制造商生产的新产品与再制造产品之间无显著差异。虽然闭环供应链在一定程度上遵循了“减量化、再循环、再利用”的原则并履行了对于环境的一部分CSR，但是越来越多的企业开始承担更多的社会责任，例如华为手机制造商与雨林保护组织RFCx合作，利用华为云AI有效检测和防止雨林盗伐等，因此假设制造商主导并承担相应的CSR投入。制造商以企业社会福利最大化作为决策目标，因此采取消费者剩余的方式来刻画制造商对于CSR的投入，即

$CS={\displaystyle {\int }_p^{p_{\max }}q\text{d}p}=\frac{{\left(a-\beta p\right)}^2}{2\beta }$ (2)

$\theta CS$ 表示制造商CSR投入时所考虑的消费者剩余程度的大小，其中 $\theta \in \left[0,1\right]$ 表示制造商承担CSR的程度， $\theta =0$ 表示制造商没有进行CSR投入， $\theta =1$ 表示制造商为完全CSR企业。

在逆向供应链中，由制造商、零售商、第三方进行产品的回收，制造商完成再制造品的制造，且废旧产品的回收质量水平m不尽相同， $0<m<1$。回收方通过回收努力时可一定程度地提升m，假设 $I\left(m\right)=k{m}^2$，其中 $k>0$ 为回收努力成本参数，且类似文献 [3] [14] 等的研究，k需满足

$k>\frac{\beta {\tau }^2{\left(c_s-a\right)}^2+\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{2\left(2-\theta \right)}$ (3)

假设回收方从消费者手中回收废旧产品的成本 $A\left(m\right)$ 与废旧产品回收质量m呈正相关，即 $A\left(m\right)=am$，其中 $a>0$ 为回收方支付给消费者的最大的单位废旧产品回收价格；制造商从回收方处回收废旧产品的单位转移价格 $B\left(m\right)$ 与废旧产品质量m呈正相关，即 $B\left(m\right)=bm,b>0$。为了保证废旧产品回收的经济性及可行性，需满足 $b>a>0$。另外， $\tau$ 为废旧产品的回收率，本研究中将其设置为外生变量。在制造商再制造产品环节，再制造产品的单位生产成本 $c_r\left(m\right)=c_n-c_{s}m$， $c_s$ 为单位产品再制造节约的最大成本。根据以上假设，得到制造商的总制造成本为

$c\left(m\right)=c_n-c_{s}m\tau$ (4)

${\pi }_{ij}$ 表示第i种回收模式中供应链成员j的经济利润， $i,j=\left\{M,R,T\right\}$，分别表示制造商回收、零售商回收、第三方回收。 $V_{iM}$ 表示第种回收模式下考虑CSR时制造商的总利润，其中 $V_{iM}=CS+{\pi }_{iM}$， $V_{iS}$ 表示第i种回收模式下考虑CSR时闭环供应链系统的总利润， $V_{iS}=CS+{\pi }_{iM}+{\pi }_{iR}+{\pi }_{iT}$.

3.2. 考虑回收质量与CSR投入的闭环供应链模型

3.2.1. 集中决策模型

首先考虑由制造商、零售商和消费者组成的闭环供应链的集中决策模型。在该模型中，闭环供应链模型的总利润由废旧产品回收质量m与零售价格p决定，此时系统利润函数表示为：

$V_{CS}=\left(p-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-am\tau \left(\alpha -\beta p\right)-k{m}^2+\theta \frac{{\left(\alpha -\beta p\right)}^2}{2\beta }$ (5)

对式(5)运用逆向归纳法求解，得到废旧产品的最优回收质量水平和最优零售价格如表1第2列结果所示。

3.2.2. 制造商回收模型

在制造商回收模型中，制造商负责新产品与再制造产品的生产及废旧产品的回收，并且进行CSR的投入零售商负责产品的销售。此时制造商、零售商的经济利润函数表达式为：

${\pi }_{MM}=\left(w-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-am\tau \left(\alpha -\beta p\right)-k{m}^2$ (6)

${\pi }_{MR}=\left(p-w\right)\left(\alpha -\beta p\right)$ (7)

制造商总利润函数表达式为：

$V_{MM}=\left(w-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-am\tau \left(\alpha -\beta p\right)-k{m}^2+\theta \frac{{\left(\alpha -\beta p\right)}^2}{2\beta }$ (8)

在此模型中，制造商以总利润最大化作为自己的决策目标，运用逆向归纳法求得制造商回收模式下的均衡结果如表1第3列结果所示。

3.2.3. 零售商回收模型

在零售商回收模型中，制造商只负责新产品与再制造产品的生产及CSR的投入，零售商除负责产品的销售外还负责废旧产品的回收。此时制造商、零售商的经济利润函数表达式：

${\pi }_{RM}=\left(w-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-bm\tau \left(\alpha -\beta p\right)$ (9)

${\pi }_{RR}=\left(p-w\right)\left(\alpha -\beta p\right)+\left(b-a\right)\left(\alpha -\beta p\right)m\tau -k{m}^2$ (10)

制造商的总利润函数表达式为：

$V_{RM}=\left(w-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-bm\tau \left(\alpha -\beta p\right)+\theta \frac{{\left(\alpha -\beta p\right)}^2}{2\beta }$ (11)

在此模型中，制造商同样以总利润最大化作为自己的决策目标，运用逆向归纳法求得零售商回收模式下的均衡结果如表1第4列结果所示。

3.2.4. 第三方回收模型

在第三方回收模型中，制造商与零售商分别负责产品的制造与销售，由第三方负责废旧产品的回收。此时制造商、零售商、第三方的经济利润函数表达式为：

${\pi }_{TM}=\left(w-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-bm\tau \left(\alpha -\beta p\right)$ (12)

${\pi }_{TR}=\left(p-w\right)\left(\alpha -\beta p\right)$ (13)

${\pi }_{TT}=\left(b-a\right)m\tau \left(\alpha -\beta p\right)-k{m}^2$ (14)

制造商的总利润函数表达式为：

$V_{TM}=\left(w-c_n+c_{s}m\tau \right)\left(\alpha -\beta p\right)-bm\tau \left(\alpha -\beta p\right)+\theta \frac{{\left(\alpha -\beta p\right)}^2}{2\beta }$ (15)

在此模型中，运用逆向归纳法求得第三方回收模式下的均衡结果如表1第5列结果所示。

4. 均衡结果分析

性质1：在零售商负责回收时，当 $b=c_s$ 时，制造商获得的利润最大.

证明：因为 $\frac{\partial V_{RM}}{\partial b}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2\left(c_s-a\right)}{2{\left(k\left(4-\theta \right)-\left(b-a\right)\beta {\tau }^2\left(c_s-a\right)\right)}^2}>0$，且 $a<b\le c_s$，所以当 $b=c_s$ 时，制造商所获得的利润 $V_{RM}$ 取得最大值。

上述性质表明，在零售商负责回收的模型中，制造商并没有通过逆向供应链的回收环节获得转移支付利润，却促进了整个闭环供应链及供应链主体利润的增加。在逆向供应链中，制造商支付给零售商转移支付的提升会使得零售商更有动机提升废旧产品的回收质量，使得闭环供应链的绿色效益及零售商的回收收益有所增加；在正向供应链中，零售商因回收收益增加更有动机通过降低产品价格来刺激消费者对于产品的需求，使得制造商及零售商的销售收益增加。因此，从正向和逆向供应链的角度考虑，在零售商回收的模型中下文将采用当 $b=c_s$ 时制造商和零售商的函数利润表达式进行讨论。

性质2：在第三方负责回收时，当 $b=\frac{a+c_s}{2}$ 时，制造商获得的利润最大.

证明：因为 $\frac{\partial V_{TM}}{\partial b}=-\frac{k{\left(\alpha -\beta c_n\right)}^2\left(2b-c_s-a\right)\beta {\tau }^2}{2\beta {\left(k\left(4-\theta \right)-\left(b-a\right)\beta {\tau }^2\left(c_s-b\right)\right)}^2}$，当 $b<\frac{a+c_s}{2}$ 时， $\frac{\partial V_{TM}}{\partial b}>0$，当 $b>\frac{a+c_s}{2}$ 时， $\frac{\partial V_{TM}}{\partial b}<0$，因此当 $b=\frac{a+c_s}{2}$ 时，制造商的利润取得最大值。

表1. 闭环供应链不同回收模式最优均衡结果

表2. 限定转移支付b时闭环供应链不同回收模式最优均衡结果

上述性质表明，在第三方负责回收的过程中，由于制造商与第三方之间不存在产品的批发与销售环节，因此制造商只能通过影响单位废旧产品的回收转移支付来影响第三方废旧产品的回收质量。当制造商的转移支付 $b=\frac{a+c_s}{2}$ 时，制造商的利润取得最大值。因此，在第三方回收的模型中下文将采用当 $b=\frac{a+c_s}{2}$ 时制造商、零售商和第三方的函数利润表达式进行讨论，整理结果如表2所示。

性质3： $\frac{\partial m_c^{*}}{\partial \theta }>0$， $\frac{\partial m_M^{*}}{\partial \theta }>0$， $\frac{\partial m_R^{*}}{\partial \theta }>0$， $\frac{\partial m_T^{*}}{\partial \theta }>0$

$\frac{\partial m_c^{*}}{\partial \tau }>0$, $\frac{\partial m_M^{*}}{\partial \tau }>0$, $\frac{\partial m_R^{*}}{\partial \tau }>0$, $\frac{\partial m_T^{*}}{\partial \tau }>0$.

证明：根据表2的均衡结果，可得

$\frac{\partial m_c^{*}}{\partial \theta }=\frac{2k\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{{\left(2k\left(2-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

与集中决策时类似，在分散决策中，同样有 $\frac{\partial m_M^{*}}{\partial \theta }>0$， $\frac{\partial m_R^{*}}{\partial \theta }>0$， $\frac{\partial m_T^{*}}{\partial \theta }>0$。

$\frac{\partial m_c^{*}}{\partial \tau }=\frac{\left(\alpha -\beta c_n\right)\left(c_s-a\right)\left(2k\left(2-\theta \right)+{\left(c_s-a\right)}^2\beta {\tau }^2\right)}{{\left(2k\left(2-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

与集中决策时类似，在分散决策中，同样有 $\frac{\partial m_M^{*}}{\partial \tau }>0$， $\frac{\partial m_R^{*}}{\partial \tau }>0$， $\frac{\partial m_T^{*}}{\partial \tau }>0$。

其中， $k>\frac{\beta {\tau }^2{\left(c_s-a\right)}^2+\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{2\left(2-\theta \right)}$，因此性质3成立。

上述性质表明，无论哪种回收模式，废旧产品的回收质量均会随着制造商承担CSR程度的增强而提升。这是因为制造商投入越多的CSR，会进一步刺激消费者需求正向增长，回收方会更加努力提升回收产品的质量来进一步提升其边际效益；并且废旧产品的回收质量还会随着回收率的增加而提升。这是因为当废旧产品的回收率提升时，在逆向供应链中因回收带来的数量优势一定程度上可以弥补回收努力成本。因此，废旧产品的回收质量会随制造商投入CSR程度及废旧产品回收率的增加而增加。

性质4： $\frac{\partial w_M^{*}}{\partial \theta }<0$， $\frac{\partial w_R^{*}}{\partial \theta }<0$， $\frac{\partial w_T^{*}}{\partial \theta }<0$，

$\frac{\partial q_c^{*}}{\partial \theta }>0$, $\frac{\partial q_M^{*}}{\partial \theta }>0$, $\frac{\partial q_R^{*}}{\partial \theta }>0$, $\frac{\partial q_T^{*}}{\partial \theta }>0$,

$\frac{\partial p_c^{*}}{\partial \theta }<0$, $\frac{\partial p_M^{*}}{\partial \theta }<0$, $\frac{\partial p_R^{*}}{\partial \theta }<0$, $\frac{\partial p_T^{*}}{\partial \theta }<0$.

证明 根据表2的均衡结果，得

$\frac{\partial w_M^{*}}{\partial \theta }=-\frac{8k^2\left(\alpha -\beta c_n\right)}{\beta {\left(2k\left(4-\theta \right)-{\left(c_s-a\right)}^2\beta {\tau }^2\right)}^2}<0$，

与制造商回收时类似，在零售商、第三方回收时，同样有 $\frac{\partial w_R^{*}}{\partial \theta }<0$， $\frac{\partial w_T^{*}}{\partial \theta }<0$。

$\frac{\partial q_c^{*}}{\partial \theta }=\frac{4k^2\left(\alpha -\beta c_n\right)}{{\left(2k\left(2-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

与集中决策时类似，在分散决策中，同样有 $\frac{\partial q_M^{*}}{\partial \theta }>0$， $\frac{\partial q_R^{*}}{\partial \theta }>0$， $\frac{\partial q_T^{*}}{\partial \theta }>0$.

$\frac{\partial p_c^{*}}{\partial \theta }=-\frac{2k\left(2k\left(\alpha -\beta c_n\right)+\alpha \left(\beta -1\right){\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(2k\left(2-\theta \right)-{\tau }^2{\left(c_s-a\right)}^2\right)}^2}<0$,

与集中决策时类似，在分散决策中，同样有 $\frac{\partial p_M^{*}}{\partial \theta }<0$， $\frac{\partial p_R^{*}}{\partial \theta }<0$， $\frac{\partial p_T^{*}}{\partial \theta }<0$。结合k的约束条件，故性质4成立。

性质4表明，无论哪种回收模式下，产品的批发价格及零售价格均会随着制造商投入CSR程度的增加而有所降低，产品需求却会随着CSR投入程度的增加而增加。在正向供应链的决策过程中，当制造商考虑较大程度的消费者剩余时，制造商的经济利润会有一定的损失，此时制造商和零售商分别通过降低批发价格及零售价格的方式来刺激市场需求，从而提升经济利润。郑本荣等 [15] 的研究表明，当零售商为主导者并负责CSR投入时零售价格会随CSR投入程度的增加而增加，这是因为其在刻画CSR时选择了以成本投入并且会影响消费者需求的方式，并且证明了适当提升零售价格对需求的负向影响小于投入CSR时对需求的正向影响，因此证明了CSR投入的必要性。本文的性质4则认为制造商CSR的投入在考虑消费者剩余的情况下会通过降低批发价格的方式从而影响零售价格。

性质5： $\frac{\partial {\pi }_{MM}^{*}}{\partial \theta }<0$， $\frac{\partial {\pi }_{RM}^{*}}{\partial \theta }<0$， $\frac{\partial {\pi }_{TM}^{*}}{\partial \theta }<0$，

$\frac{\partial {\pi }_{MR}^{*}}{\partial \theta }>0$, $\frac{\partial {\pi }_{RR}^{*}}{\partial \theta }>0$, $\frac{\partial {\pi }_{TR}^{*}}{\partial \theta }>0$, $\frac{\partial {\pi }_{TT}^{*}}{\partial \theta }>0$,

$\frac{\partial V_{MM}^{*}}{\partial \theta }>0$, $\frac{\partial V_{RM}^{*}}{\partial \theta }>0$, $\frac{\partial V_{TM}^{*}}{\partial \theta }>0$,

$\frac{\partial V_{CS}^{*}}{\partial \theta }>0$, $\frac{\partial V_{MS}^{*}}{\partial \theta }>0$, $\frac{\partial V_{RS}^{*}}{\partial \theta }>0$, $\frac{\partial V_{TS}^{*}}{\partial \theta }>0$.

证明：根据表2的均衡结果，

$\frac{\partial {\pi }_{MM}^{*}}{\partial \theta }=-\frac{8k^3\theta {\left(\alpha -\beta c_n\right)}^2}{\beta {\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^3}<0$,

与制造商回收时类似，当零售商、第三方回收时，有 $\frac{\partial {\pi }_{RM}^{*}}{\partial \theta }<0$， $\frac{\partial {\pi }_{TM}^{*}}{\partial \theta }<0$。

$\frac{\partial {\pi }_{MR}^{*}}{\partial \theta }=\frac{16k^3{\left(\alpha -\beta c_n\right)}^2}{\beta {\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^3}>0$,

与制造商回收时类似，当零售商、第三方回收时，有 $\frac{\partial {\pi }_{RR}^{*}}{\partial \theta }>0$， $\frac{\partial {\pi }_{TR}^{*}}{\partial \theta }>0$。

$\frac{\partial {\pi }_{TT}^{*}}{\partial \theta }=\frac{8k^2{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2}{{\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^3}>0$

$\frac{\partial V_{MM}^{*}}{\partial \theta }=\frac{2k^2{\left(\alpha -\beta c_n\right)}^2}{\beta {\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(-a+c_s\right)}^2\right)}^2}>0$

与制造商回收时类似，当零售商、第三方回收时，有 $\frac{\partial V_{RM}^{*}}{\partial \theta }>0$， $\frac{\partial V_{TM}^{*}}{\partial \theta }>0$。

$\frac{\partial V_{CS}^{*}}{\partial \theta }=\frac{4k^2{\left(\alpha -\beta c_n\right)}^2}{\beta {\left(2k\left(2-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^3}>0$

与集中决策时类似，在分散决策中，同样有 $\frac{\partial V_{MS}^{*}}{\partial \theta }>0$， $\frac{\partial V_{RS}^{*}}{\partial \theta }>0$， $\frac{\partial V_{TS}^{*}}{\partial \theta }>0$。结合k的约束条件，故性质5成立。

性质5表明，无论哪种回收模式，制造商的经济利润均会随着其承担CSR程度的增强而降低，但当制造商以社会福利最大化作为决策目标时，闭环供应链主体的经济利润及系统总利润会随着CSR程度的增强而提升。这是因为制造商作为渠道领导者在进行CSR投入时不仅能够有效促进废旧产品回收质量的提升，还降低了产品生产过程中的平均成本，因此制造商有动机降低批发价格从而刺激零售商的需求，零售商也会降低零售价格来刺激消费者需求，使得整个闭环供应链系统良性循环。

以上几点性质表明，当制造商承担CSR时，无论哪种回收模式，废旧产品的回收质量、产品的市场需求会随着CSR程度的增加而增加，而产品的批发价格及零售价格均会随着CSR程度的增加而降低，虽然制造商的经济利润会因CSR的投入而降低，但是对于整个闭环供应链系统及其他主体而言是有益的。

定理1：① 当 $0<\theta <{\theta }^{*}$ 时，有 $w_R^{*}>w_T^{*}>w_M^{*}$ ；当 ${\theta }^{*}\le \theta <1$ 时，有 $w_T^{*}>w_R^{*}>w_M^{*}$，其中 ${\theta }^{*}=1-\frac{\beta {\tau }^2{\left(c_s-a\right)}^2}{4k}$。

② $m_c^{*}>m_R^{*}>m_M^{*}>m_T^{*}$ ;

$q_c^{*}>q_R^{*}>q_M^{*}>q_T^{*}$ ;

$p_c^{*}<p_R^{*}<p_M^{*}<p_T^{*}$.

证明：① 根据表2的均衡结果，易得

$w_T^{*}-w_M^{*}=\frac{4k{\tau }^2\left(\alpha -\beta c_n\right){\left(c_s-a\right)}^2}{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}>0$,

$w_R^{*}-w_M^{*}=\frac{{\tau }^2\left(\alpha -\beta c_n\right){\left(c_s-a\right)}^2\left(2k\left(2-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{2\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}>0$,

$w_T^{*}-w_R^{*}=-\frac{{\tau }^2\left(\alpha -\beta c_n\right){\left(c_s-a\right)}^2\left(4k\left(1-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{2\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}=f_1\left(\theta \right)$,

求得 ${f^{\prime }}_1\left(\theta \right)=\frac{k{\tau }^2\left(\alpha -\beta c_n\right){\left(c_s-a\right)}^2\left(16k^2\left(4-\theta \right)\left(2+\theta \right)-4k\beta {\tau }^2\left(7+2\theta \right){\left(c_s-a\right)}^2-{\beta }^2{\tau }^4{\left(c_s-a\right)}^4\right)}{2{\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2{\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$。

故 $f_1\left(\theta \right)$ 在 $\theta \in \left(0,1\right)$ 单调递增。令 $f_1\left(\theta \right)=0$ 求得 ${\theta }^{*}=1-\frac{\beta {\tau }^2{\left(c_s-a\right)}^2}{4k}$，所以当 $0<\theta <{\theta }^{*}$ 时，有 $w_R^{*}>w_T^{*}>w_M^{*}$ ；当 ${\theta }^{*}\le \theta <1$ 时，有 $w_T^{*}>w_R^{*}>w_M^{*}$，故定理1得证。

定理1表明，在制造商回收时产品的批发价格最低。此时制造商和零售商之间只能通过产品的销售来进行博弈，相较于其他回收模式而言，制造商有更大的动机降低产品的批发价格来刺激零售商的需求从而提升自己的经济利润。当回收方转变为零售商或第三方时，制造商的批发价格相对自己进行回收而言会略高。不难发现，虽然零售商回收时产品批发价格高于制造商回收模式，但是其废旧产品的回收质量、市场需求及零售价格均优于制造商回收模式及第三方回收模式。由性质1可知制造商若想实现总利润最大化，需将逆向供应链中获得的成本优势全部转移给零售商，此时的零售商有动机通过提升废旧产品的回收质量来回馈制造商并使自己获益；性质4表明制造商的批发价格会随CSR投入程度的增强而降低，此时零售商也会通过降低产品零售价格来刺激市场需求，实现正向供应链中经济利润最大化的目标。因此，在分散决策模式下，零售商回收时废旧产品回收质量、零售价格、市场需求均为最优。

定理2：① ${\pi }_{RR}^{*}>{\pi }_{MR}^{*}>{\pi }_{TR}^{*}$

② 当 $k>\max \left\{\frac{\beta {\tau }^2{\left(c_s-a\right)}^2+\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{2\left(2-\theta \right)},\frac{3\beta {\tau }^2{\left(c_s-a\right)}^2\left(2-\theta \right)}{\left(4-\theta \right)\left(4-3\theta \right)}\right\}$ 时，有 ${\pi }_{RM}^{*}>{\pi }_{MM}^{*}>{\pi }_{TM}^{*}$ ；

③ $V_{RM}^{*}>V_{MM}^{*}>V_{TM}^{*}$。

证明：根据表2的均衡结果，证明过程如下：

① ${\pi }_{MR}^{*}-{\pi }_{TR}^{*}=\frac{4k^2{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2\left(8k\left(4-\theta \right)-3\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{{\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

${\pi }_{RR}^{*}-{\pi }_{MR}^{*}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2\left(4k^2\left(4-\theta \right)\theta +4k\left(1-\theta \right)\beta {\tau }^2{\left(c_s-a\right)}^2-{\beta }^2{\tau }^4{\left(c_s-a\right)}^4\right)}{4{\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

故有 ${\pi }_{RR}^{*}>{\pi }_{MR}^{*}>{\pi }_{TR}^{*}$。

② ${\pi }_{MM}^{*}-{\pi }_{TM}^{*}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2\left(8k^2\left(4-\theta \right)\left(4-3\theta \right)-12k\left(2-\theta \right)\beta {\tau }^2{\left(c_s-a\right)}^2+{\beta }^2{\tau }^4{\left(c_s-a\right)}^4\right)}{{\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$

故有 ${\pi }_{MM}^{*}>{\pi }_{TM}^{*}$ ；

${\pi }_{RM}^{*}-{\pi }_{MM}^{*}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2\left(2k\left(k\left(4-\theta \right)\left(4-3\theta \right)-3\left(2-\theta \right)\beta {\tau }^2{\left(c_s-a\right)}^2\right)+{\beta }^2{\tau }^4{\left(c_s-a\right)}^4\right)}{{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^{2}2{\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}$

由上式可知， ${\pi }_{RM}^{*}$ 与 ${\pi }_{MM}^{*}$ 的大小取决于 $k\left(4-\theta \right)\left(4-3\theta \right)-3\left(2-\theta \right)\beta {\tau }^2{\left(c_s-a\right)}^2$，结合k的约束条件，当 $k>\max \left\{\frac{\beta {\tau }^2{\left(c_s-a\right)}^2+\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{2\left(2-\theta \right)},\frac{3\beta {\tau }^2{\left(c_s-a\right)}^2\left(2-\theta \right)}{\left(4-\theta \right)\left(4-3\theta \right)}\right\}$ 时，有 ${\pi }_{RM}^{*}>{\pi }_{MM}^{*}>{\pi }_{TM}^{*}$。

③ $V_{MM}^{*}-V_{TM}^{*}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2}{\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}>0$， $V_{RM}^{*}-V_{MM}^{*}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2}{2\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}>0$，故有 $V_{RM}^{*}>V_{MM}^{*}>V_{TM}^{*}$。

以上，定理2得证。

定理2表明，在分散决策的三种模式中，零售商回收时零售商的经济利润及制造商的总利润总是最大的，第三方回收时总是最小的。这是因为零售商回收时利润由正向供应链的销售收入及逆向供应链的回收收入所得，且定理1表明，无论是产品的零售价格、市场需求还是废旧产品的回收质量，在零售商回收时总是最优的，故零售商的经济利润在自身回收时达到最优。与此同时，最优的市场需求及废旧产品的回收质量会使得制造商获益，因此当制造商的总利润也是在零售商回收时达到最优。在第三方回收模式中，因废旧产品回收质量较低无法给制造商带来明显的成本优势，制造商会通过提升批发价格来提升自己的边际收益，间接影响了零售商的经济利润。从闭环供应链各主体决策目标来看，零售商回收模式优于其他两种模式。

定理3：当 $k>\max \left\{\frac{\beta {\tau }^2{\left(c_s-a\right)}^2+\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{2\left(2-\theta \right)},\frac{\beta {\tau }^2\left(10-\theta \right){\left(c_s-a\right)}^2}{8\left(4-\theta \right)}\right\}$ 时，有 $V_{CS}^{*}>V_{RS}^{*}>V_{MS}^{*}>V_{TS}^{*}$。

证明：根据表2的均衡结果，易得 $V_{CS}^{*}>V_{MS}^{*},V_{CS}^{*}>V_{RS}^{*},V_{CS}^{*}>V_{TS}^{*}$，故比较三种回收模式下系统的总利润即可。

$V_{MS}^{*}-V_{TS}^{*}=\frac{2k^2{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2\left(2k\left(12-\theta \right)\left(4-\theta \right)-\beta {\tau }^2\left(10-\theta \right){\left(c_s-a\right)}^2\right)}{{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2{\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$，即 $V_{MS}^{*}>V_{TS}^{*}$。

$V_{RS}^{*}-V_{MS}^{*}=\frac{k{\tau }^2{\left(\alpha -\beta c_n\right)}^2{\left(c_s-a\right)}^2\left(2k\left(8k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\left(10-\theta \right)\right)+{\beta }^2{\tau }^4{\left(c_s-a\right)}^4\right)}{4{\left(k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2{\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}$，

由上式可知， $V_{RS}^{*}$ 与 $V_{MS}^{*}$ 的大小取决于 $k\left(4-\theta \right)-2\beta {\tau }^2{\left(c_s-a\right)}^2\left(10-\theta \right)$，结合k的约束条件，所以当 $k>\max \left\{\frac{\beta {\tau }^2{\left(c_s-a\right)}^2+\tau \left(\alpha -\beta c_n\right)\left(c_s-a\right)}{2\left(2-\theta \right)},\frac{\beta {\tau }^2\left(10-\theta \right){\left(c_s-a\right)}^2}{8\left(4-\theta \right)}\right\}$ 时，有 $V_{CS}^{*}>V_{RS}^{*}>V_{MS}^{*}>V_{TS}^{*}$。

定理3表明，在制造商进行CSR投入时，集中决策下系统的总利润总是高于分散决策下系统的总利润。在分散决策中，当努力成本系数k较大时，零售商回收模式的系统总利润总是高于其他两种回收模式下的总利润。综合定理2来看，零售商回收模式中零售商的经济利润和制造商的总利润总是最大的，因此零售商回收模式下系统总利润最大也是合理的。

Savaskan等 [3] 的研究表明制造商主导的闭环供应链系统中零售商回收模式下系统及各主体的利润总是高于其他两种回收模式，姚锋敏等 [16] 的研究则在考虑制造商为主导者且投入CSR时零售商回收渠道结构的最优性。本文则在考虑回收质量差异的基础上，研究了回收质量与回收率及CSR水平对系统及各主体利润的影响，进一步补充验证了零售商回收模式的最优性。

定理4：① 无论哪种回收模式，当制造商以社会福利最大化为目标时，其利润总是大于零售商或第三方的经济利润；

② 在制造商或零售商负责回收时，当 $0<\theta <{\theta }^{**}$ 时，有 ${\pi }_{MM}^{*}>{\pi }_{MR}^{*}$ ( ${\pi }_{RM}^{*}>{\pi }_{RR}^{*}$ )；当 ${\theta }^{**}\le \theta <1$ 时，有 ${\pi }_{MR}^{*}>{\pi }_{MM}^{*}$，( ${\pi }_{RR}^{*}>{\pi }_{RM}^{*}$ )，其中 ${\theta }^{**}=1-\frac{\beta {\tau }^2{\left(c_s-a\right)}^2}{4k}$ ；在第三方负责回收时，当 $0<\theta <{\theta }^{***}$ 时，有 ${\pi }_{TM}^{*}>{\pi }_{TR}^{*}>{\pi }_{TT}^{*}$ ；当 ${\theta }^{***}\le \theta <1$ 时，有 ${\pi }_{TR}^{*}>{\pi }_{TM}^{*}>{\pi }_{TT}^{*}$，其中 ${\theta }^{***}=1-\frac{\beta {\tau }^2{\left(c_s-a\right)}^2}{8k}$。

证明：① 根据表2的均衡结果，证明过程如下：

当第三方负责回收时，

$V_{TM}^{*}-{\pi }_{TR}^{*}=\frac{2k{\left(\alpha -\beta c_n\right)}^2\left(4k\left(2-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

$V_{TM}^{*}-{\pi }_{TT}^{*}=\frac{k{\left(\alpha -\beta c_n\right)}^2\left(8k\left(4-\theta \right)-3\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

制造商回收模式及零售商回收模式同理。

② 根据表2的均衡结果，证明过程如下：

当制造商负责回收时，

${\pi }_{MR}^{*}-{\pi }_{MM}^{*}=-\frac{k{\left(\alpha -\beta c_n\right)}^2\left(4k\left(1-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}=f_2\left(\theta \right)$,

对 $f_2\left(\theta \right)$ 进行求导可得 ${f^{\prime }}_2\left(\theta \right)=\frac{8k^3\left(2+\theta \right){\left(\alpha -\beta c_n\right)}^2}{\beta {\left(2k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^3}>0$，因此 $f_2\left(\theta \right)$ 在 $\theta \in \left(0,1\right)$ 单调递增，故令 $f_2\left(\theta \right)=0$ 可求得 ${\theta }^{**}=1-\frac{\beta {\tau }^2{\left(c_s-a\right)}^2}{4k}$。所以当 $0<\theta <{\theta }^{**}$ 时，有 ${\pi }_{MM}^{*}>{\pi }_{MR}^{*}$ ；当 ${\theta }^{**}\le \theta <1$ 时，有 ${\pi }_{MR}^{*}>{\pi }_{MM}^{*}$。

当零售商负责回收时， ${\pi }_{RR}^{*}$ 与 ${\pi }_{RM}^{*}$ 较过程同制造商回收时相同，此处省略。

当第三方负责回收时，

${\pi }_{TR}^{*}-{\pi }_{TT}^{*}=\frac{k{\left(\alpha -\beta c_n\right)}^2\left(16k-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

${\pi }_{TM}^{*}-{\pi }_{TT}^{*}=\frac{k{\left(\alpha -\beta c_n\right)}^2\left(16k\left(2-\theta \right)-3\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}>0$,

${\pi }_{TR}^{*}-{\pi }_{TM}^{*}=\frac{2k{\left(\alpha -\beta c_n\right)}^2\left(8k\left(\theta -1\right)+\beta {\tau }^2{\left(c_s-a\right)}^2\right)}{\beta {\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(c_s-a\right)}^2\right)}^2}=f_3\left(\theta \right)$,

对 $f_3\left(\theta \right)$ 进行求导可得 ${f^{\prime }}_3\left(\theta \right)=\frac{64k^3\left(2+\theta \right){\left(\alpha -\beta c_n\right)}^2}{\beta {\left(4k\left(4-\theta \right)-\beta {\tau }^2{\left(a-c_s\right)}^2\right)}^3}>0$，因此 $f_3\left(\theta \right)$ 在 $\theta \in \left(0,1\right)$ 单调递增，故令 $f_3\left(\theta \right)=0$ 可求得 ${\theta }^{***}=1-\frac{\beta {\tau }^2{\left(c_s-a\right)}^2}{8k}$。所以当 $0<\theta <{\theta }^{***}$ 时，有 ${\pi }_{TM}^{*}>{\pi }_{TR}^{*}>{\pi }_{TT}^{*}$ ；当 ${\theta }^{***}\le \theta <1$ 时，有 ${\pi }_{TR}^{*}>{\pi }_{TM}^{*}>{\pi }_{TT}^{*}$。

以上，定理4得证。

定理4表明，当制造商以社会福利最大化作为自己的决策目标时，无论哪种回收模式中，其利润总是优于零售商及第三方，这是因为制造商考虑了一定程度的消费者剩余。当考虑程度较低时，无论哪种模式下，制造商经济利润总是高于零售商及第三方；当考虑程度较高时，自身经济利润受影响较大会低于零售商的利润。因此结合定理3从系统利润及闭环供应链各主体利润来看，零售商回收模式相对而言是最优的。Song L等 [17] 在研究零售商作为渠道领导者且进行CSR投入时，零售商所获取的利润总是会高于跟随者，且与CSR投入水平无关。本文则表明制造商作为渠道领导者时，无论投入CSR水平高低其总利润总是会高于零售商的经济利润，但是当CSR投入水平处于较高范围时，会存在零售商经济利润高于追随者的情况，这一结论与姚锋敏 [18] 等的研究一致。

定理1至定理4表明，在制造商进行CSR投入时，零售商回收模式下废旧产品的回收质量、新产品的需求及零售价格较其他两种回收模式而言均是最优的，并且这将直接影响零售商回收时闭环供应链总利润及各主体利润相对最优性。

5. 数值仿真及实证分析

5.1. 数值仿真分析

本节将通过数值仿真的方法对文中的主要定理进行验证和分析。参考相关文献，假设相关参数： $\alpha =250$， $\beta =1$， $\tau =0.7$， $a=30$， $c_n=100$， $c_s=60$， $k=1000$。

由图1可以看出，在制造商为渠道领导者并且进行CSR投入的闭环供应链中，无论哪种回收模式，废旧产品的回收质量都会随着制造商投入CSR程度的增强而提升，在分散决策中零售商回收模式下提升的更为明显，这也进一步验证了性质3。

Figure 1. Recovery quality level of three recovery modes under different CSR levels

图1. 不同CSR水平下三种回收模式的回收质量水平

图2展示了在三种不同回收模式下，制造商投入CSR水平与制造商、零售商利润之间的关系。仿真结果表明，制造商的总利润及零售商的经济利润会随着CSR投入程度的增强而逐渐上升，但制造商的经济利润却在不断下降。无论哪种回收模式下，当制造商投入CSR程度较小时，制造商的经济利润始终高于零售商的经济利润；当CSR投入程度较大时，零售商的经济利润增幅明显。可以看出，当零售商负责闭环供应链系统的回收时，制造商的经济利润和制造商的总利润、零售商的经济利润总是优于其他两种回收模式。由此可见，在考虑回收质量存在差异的闭环供应链系统中，当制造商负责CSR投入时，零售商回收模式为最优选择。这进一步验证了本文的性质5、定理2及定理3。

Figure 2. Profit comparison of three recovery models under different CSR levels

图2. 不同CSR水平下三种回收模式利润比较

5.2. 实证分析

自2019年全球疫情爆发以来，居家办公、上课、娱乐等需求驱动3C产业快速崛起，然而该行业高速发展的同时也因废旧电子产品的不当处置给环境带来了不可逆的伤害。在3C产业中，联想集团的产品覆盖了计算机类、通信等领域，并且在计算机类的市场份额较为突出；且其作为3C类产品的供应商具备专业且完善的回收平台，与零售商、第三方回收商均签订了产品回收的战略合作协议，实现了全方位多通道地构建3C市场绿色闭环供应链。因此本小节选择联想集团所在的闭环供应链进行实证分析从而进一步验证本文结论。基于由制造商联想集团主导并进行CSR投入的闭环供应链系统背景，并分别研究了联想、苏宁易购、“有得卖”平台作为回收方三种回收模式对于整个供应链成员及系统的影响。假设联想电脑的市场最大规模为 $\alpha =\text{3400}$，每生产一台新电脑的平均单位生产成本 $c_n=\text{2800}$，再制造产品的平均生产成本 $c_s=\text{2000}$，支付给消费者的最大回收价格 $a=\text{600}$，回收成本系数 $k=\text{250000}$，消费者对价格的敏感系数 $\beta =\text{1}$，回收率 $\tau =0.4$，联想集团承担CSR程度 $\theta =0.75$。

Table 3. Comparison of the best recycling quality and retail price of waste products under three recycling modes

表3. 三种回收模式下最优废旧产品回收质量及零售价格比较

表2及图3的结果表明，在联想集团负责CSR投入并主导的闭环供应链系统中，零售商苏宁易购平台回收时新产品的零售价格、废旧产品的回收质量及制造商和零售商的利润明显优于其他两种回收模式。由于零售商可以和消费者直接接触，所以当零售商投入一定的回收努力成本时，其回收效果较其他两种回收方式而言会更好，即回收质量会更高。与第三方“有的卖”平台回收相比，联想集团自身的回收模式也能取得不错的效果。这是因为联想集团进行回收时，其在回收过程中可以最大程度地节省回收成本从而降低平均生产成本。第三方平台进行回收时取得的效果相对而言是最差的。虽然第三方平台较其他两种回收模式而言有着更为专业的鉴定方式和定价体系，但是其只有逆向供应链回收一种渠道盈利，且渠道话语权较低。

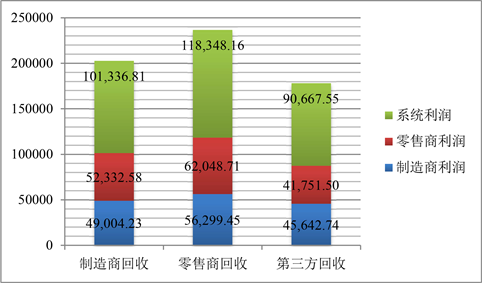
Figure 3. Profit comparison of closed-loop supply chain entities under different recovery modes

图3. 不同回收模式下闭环供应链主体利润比较

事实上，联想集团采用多种回收渠道进行回收，当其采用组合回收方式进行回收时可以多渠道全方位的利用以旧换新模式刺激消费者对新产品的需求从而获得更好的用户粘性。本章基于联想集团采用单一渠道回收模式假设，比较得出了三种回收模式下零售商回收模式对于整个闭环供应链系统的最优性这一结论。

6. 结论

本文在考虑废旧电子产品回收时回收质量存在差异的基础上，构建了制造商主导且进行CSR投入的多级闭环供应链模型，研究了不同回收模式下制造商CSR投入对废旧产品回收质量及供应链主体利润的影响，得到以下主要结论：

1) 无论在哪种回收模式下，制造商进行CSR的投入均有利于废旧产品回收质量的提升，尽管此时制造商的成本优势会转移至回收方，但是其对于正向供应链中市场需求的影响是正向的；且回收率的提升在一定程度上也能够提升废旧产品的回收质量；

2) 无论在哪种回收模式下，随着制造商CSR投入程度的不断增强，为挽回一定经济利润损失的制造商会降低产品的批发价格，由此零售商决定的产品的零售价格会逐渐下降，从而有助于扩大市场需求；

3) 无论在哪种回收模式下，随着制造商CSR投入程度的不断增强，在正向供应链中由于市场需求的提升制造商的总利润、零售商的利润及系统的总利润均会有显著提升，但是会损害制造商自身的经济利润；

4) 无论是从降低零售价格能够更好地刺激市场需求角度，还是从提升废旧产品的回收质量使得制造商及零售商经济利润有所提升的角度，当制造商进行CSR投入时零售商回收模式是最优的，第三方回收模式效果是最差的。

本文的研究基于信息对称的假设只考虑了制造商在进行CSR投入时选择单一回收渠道进行回收的闭环供应链模型，然而现实生活中存在制造商采用多渠道进行回收的案例，且因废旧产品回收质量水平的不同在各种回收渠道之间存在竞争关系。在之后的研究中可以进一步研究多回收渠道结合且存在竞争关系的闭环供应链模型中回收模式的不同对供应链主体利润的影响。