旱作区阳离子交换量土壤转换函数的研究

Study on Pedo-Transfer Functions of Cation Exchange Capacity in Dry Farming Region

摘要: 为减少大范围测定阳离子交换量(cation exchange capacity, CEC)工作量，探寻一种利用较容易测定的土壤理化性质预测CEC简单、高效的方法。本文基于旱作区152个表层0~10 cm土壤的pH、质地、有机质等数据，建立BP神经网络、支持向量机、多元线性回归3种CEC土壤转换函数，并比较分析了各方法的预测精度和敏感性。结果表明，CEC主要受有机质、黏粒的影响且呈明显的正相关关系；支持向量机预测精度最高，其决定系数(R² = 0.58)、效率系数(E = 0.57)均高于BP神经网络和多元线性回归，均方根误差(RMSE = 5.41)均低于其他模型，多元线性回归模型预测精度最低。支持向量机方法在旱作区内能够较好地预测阳离子交换量。

Abstract: In order to reduce the workload of large-scale determination of cation exchange capacity (CEC), a simple and efficient method for predicting CEC by using easily measured soil physical and chemical properties was explored. Researcher have used different input soil properties to derive pedo-transfer functions (PTFs) to predict soil CEC. Based on the pH, texture and organic matter (OM) of 152 topsoil (0~10 cm) samples in dry farming region, the CEC soil transfer function was established by back propagation neural network (BP-NN), support vector machine (SVM) and multiple linear regression (MLR), and the prediction accuracy and sensitivity of each method were compared and analyzed. The results showed that CEC was mainly positively correlated with OM and clay. The prediction accuracy of SVM was the highest, with its decision coefficient (R² = 0.58) and efficiency coefficient (E = 0.57) higher than BP-NN and MLR. The root mean square error of SVM (RMSE = 5.41) is lower than other models, and MLR model has the lowest prediction accuracy. SVM method can better predict cation exchange capacity in dry farming.

1. 引言

阳离子交换量(CEC)作为衡量土壤肥力和生产力的重要指标，它能够直接反应土壤的保肥性能和缓冲性能。我国东北和黄淮海旱地作物种植区是重要商品粮基地，从北到南土壤类型复杂，土壤性质差异性大 [1] ，准确获取CEC对制定土壤肥力调控措施有重要意义。然而，传统的CEC测定方法存在着成本高、耗时长、工作繁重等缺点，利用易测定的土壤基本理化指标建立土壤转换函数(PTFs)间接预测CEC是一种高效、快捷的方法 [2] 。常用的指标为pH、土壤有机质、黏粒含量等 [3] [4] 。建立PTFs常用方法是人工神经网络、多元线性 [5] 与非线性回归、分类树回归等方法。人工神经网络可以从有限的数据集中通过相关性学习复杂的函数关系，并根据环境的变化对模型进行调整，构建非线性、多变量动态系统黑箱模型 [6] 。BP神经网络因其结构简单、操作性强、收敛速度快等优点广泛用于非线性建模、函数逼近、模式识别等方面 [7] 。Vapnik提出支持向量机(SVM)可以代替人工神经网络，它是非线性分类、回归和时间序列预测的有力工具 [8] 。

为此，本文以旱作区表层0~10 cm土壤为研究对象，建立了BP神经网络(BP-NN)、支持向量机、多元线性回归(MLR)三种的PTFs，通过比较分析三种模型的精度和敏感性，提出适用于旱作区预测CEC的PTFs函数，以期为合理获取旱作区的土壤参数提供依据，也为土壤、作物等模型参数获取提供理论支持。

本文的组织结构如下：第2节介绍研究区域数据来源与处理、研究方法；第3节介绍SVM、BP-NN、MLR三种PTFs的模型构建结果及精度检验与敏感性分析；第4节介绍了输入变量对PTFs预测精度的影响及三种PTFs在旱作区的有效性与适用性；在第5节给出了结论与展望。

2. 材料与方法

2.1. 研究区域

旱作区以地形坡度小于5˚、1 km²网格内旱地占耕地比在40%以上作为划分依据，界定其内涵与范围。该区域涵盖东北黑龙江、辽宁和吉林三省，以及黄淮海的河北、北京、山东、河南、安徽五省市，主要种植玉米、小麦等粮食作物和大豆、甜菜等经济作物，是中国重要商品粮基地。地理坐标为113˚03'51''~134˚5'31''E，32˚21'17''~48˚57'51''N，研究区属温带季风气候，年均气温2.4℃~16.1℃，年均降水量435.9~957.4 mm，土壤类型主要包括潮土、褐土、黑钙土、黑土、砂姜黑土、棕壤、暗棕壤。

2.2. 数据来源与处理

研究区采用网格均匀布点和分层抽样相结合方法的布点采样。该方法在考虑空间自相关基础上，采用分层抽样避免随机采样中样点的空间聚集，考虑环境相似性，可使用少量样点代表相似的环境下土壤的信息，提高采样效率。采样网格大小为15 km × 15 km，在此基础上根据土壤类型、土壤颗粒组成与耕地质量等级等进行分层抽样。采样时间为2017年4~6月，共取152个0~10 cm表层土壤样品，每个样点用GPS记录其位置，样点分布如下(见图1)。每个样点随机设置3个重复。样品经自然风干后混合过2 mm筛备用。土壤质地采用激光粒度分析仪测定，土壤颗粒分级标准采用美国制。土壤有机质采用重铬酸钾外加热法测定。土壤pH采用电位法测定。土壤CEC采用乙酸铵交换法、乙酸钠–火焰光度法测定。

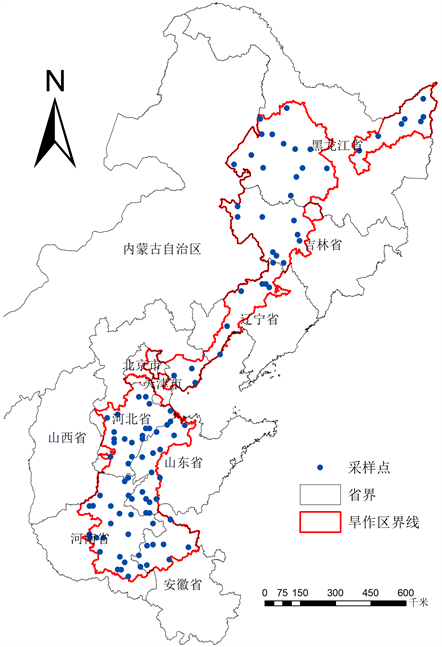
Figure 1. Location and sample distribution of the study area

图1. 研究区位置及样点分布

样点各数据的描述性统计、相关分析以及多元线性回归采用SPSS软件，BP-NN、SVM建模采用Matlab软件。

因各个变量单位不同，为取消各数据间数量级差别，避免因为输入、输出数据数量级别差别较大而造成预测误差较大 [9] ，在预测前首先要将数据集通过公式(1)进行归一化处理。

$X_k=\frac{x_k-x_{\min }}{x_{\max }-x_{\min }}$ (1)

式中：x_min为数据序列中最小值；x_max为数据序列中最大值；X_k为归一化后的值。

最后将模型输出结果进行反归一化。

2.3. 研究方法

在本研究中选择的自变量为：pH、砂粒、黏粒、有机质含量，因变量为CEC，这与学者们的研究 [3] [4] [9] 一致。

2.3.1. 多元线性回归

在MLR分析中，5%显著水平下的预测变量为主要变量 [2] 。在此回归中将有机质、砂粒、粉粒、黏粒含量和pH作为自变量，并将CEC作为因变量利用SPSS软件按照公式(2)形式推导回归模型。

$\text{y=}{b}_1{x}_1+b_2{x}_2+\dots +b_n{x}_n+c$ (2)

式中： $b_{\text{1}},b_2,\cdots ,b_n$ 为自变量，y为因变量，c为常数。

2.3.2. BP神经网络

神经网络是一种自适应系统，它从输入和输出数据集学习关系，并能预测具有与输入集相似特征的数据集 [10] 。最初是为生物神经系统的性能建模而设计的 [11] 。BP-NN是一种多层前馈神经网络，该网络主要包括三层：输入层、隐含层、输出层，每层均由神经元组成，并通过连接权重和前一层进行连接。网络学习目的是获得恰当的权、阈值，由正向和反向传播两部分组成 [12] 。

在BP-NN中，隐含层节点数的选择对BP神经网络预测精度有较大的影响：节点数太少，网络不能很好地学习，需要增加训练的次数，精度也受影响；节点数太多，训练时间增加，网络容易过拟合 [13] 。通过公式(3)选择最佳隐含层节点数：

$l<\sqrt{\left(i+j\right)}+a$ (3)

式中：a为0~10之间的常数。

隐含层节点数选择首先是参考公式来确定节点数的大概范围，然后用试凑法确定最佳的节点数。

2.3.3. 支持向量机

支持向量机是建立在统计学习理论和结构风险最小化原则基础上的机器学习方法。它能够根据有限的样本信息，在模型复杂性和学习能力之间寻求最佳折衷 [14] 。SVM提供了一种使用内核函数将超平面表面拟合到训练数据的机制。

对于本研究的回归情况，首先执行从输入空间到高维特征空间的映射，然后使用–不敏感损失通过特征空间中的超平面执行线性回归。

对于给定的n个训练集，分别为 $\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_n,y_n\right)$ 其中x是输入向量，y是对应的输出值，回归的SVM估计量f如公式(4)所示：

$f=\omega \cdot \phi \left(x\right)+b={\displaystyle {\sum }_{i=1}^n\left({\alpha }_i-{\alpha }_i^{\ast }\right)k\left(x\cdot x_i\right)+b}$ (4)

式中：w是权重向量，b为偏差，“∙”表示点集，φ为非线性映射函数， ${\alpha }_i,{\alpha }_i^{\ast }$ 为拉格朗日乘子， $k\left(x\cdot x_i\right)$ 为核函数。

2.3.4. 模型精度检验

本文以平均绝对误差(MAE)、决定系数(R²)、均方根误差(RMSE)及Nash-Sutcliff效率系数(E)四个指标来评估模型预测精度。其中MAE越小预测精度越高；R²越大预测精度越高，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比越高；RMSE可以对模型的拟合优度提供均衡评估，RMSE越小预测精度越高；E的范围从−∞到1，当E = 1时获得的模型是最优拟合。如公式(5)~(8)所示：

$\text{MAE}=\frac{{\displaystyle {\sum }_{i=1}^n\left|\left({\text{CEC}}_p-{\text{CEC}}_m\right)\right|}}{n}$ (5)

$R^2=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left({\text{CEC}}_m-{\overline{\text{CEC}}}_p\right)}^2}}{{{\displaystyle {\sum }_{i=1}^n\left({\text{CEC}}_m-{\overline{\text{CEC}}}_m\right)}}^2}$ (6)

$\text{RMSE}=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{\left({\left(CE{C}_m\right)}_i-{\left(CE{C}_p\right)}_i\right)}^2}}{n}}$ (7)

$E=1-\frac{{\displaystyle {\sum }_{i=1}^n{\left[{\left({\text{CEC}}_m\right)}_i-{\left({\text{CEC}}_p\right)}_i\right]}^2}}{{{\displaystyle {\sum }_{i=1}^n\left[{\left({\text{CEC}}_m\right)}_i-\left({\overline{\text{CEC}}}_m\right)\right]}}^2}$ (8)

式中：下标“m”和“p”代表实测值和预测值；i为第i个样本；n是样本数。

2.3.5. 模型敏感性分析

敏感性分析可以确定参数对模型模拟结果影响的大小。本文用回归分析法对BP-NN、SVM模型中输入的土壤参数对CEC的影响进行全局敏感性分析，其中将标准回归系数表示各参数的敏感性。

3. 结果与分析

3.1. 描述性统计分析

样本集随机将75%的样本分为训练集，剩余部分为测试集，样本集的土壤理化性质变异系数为19.89%~75.14% (见表1)，其中有机质变异系数约为CEC变异系数的1.6倍。根据Nielsen [15] 和李哈滨 [16] 对变异程度的定义，变异系数 < 10%为弱变异性，变异系数介于10%与100%之间为中等变异性，变异系数 > 100%为强变异性。研究区域内样本集的pH、砂粒、粉粒、黏粒含量、有机质、CEC等6种土壤理化性质均处于中等强度变异水平。样本集、训练集、测试集中土壤理化性质具有相似的变异系数。

3.2. 相关性分析

对样本集的各变量与CEC之间进行相关性分析。在p < 0.01情况下，有机质、黏粒和砂粒含量与CEC相关系数分别为：0.656、0.449、−0.438，有机质、黏粒含量与CEC存在明显的正相关关系，而砂粒含量与CEC之间存在明显的负相关关系(见表2)。砂粒与粉粒含量之间相关系数为−0.994，表明它们存在着极为强烈的负相关关系，这是因为在该研究区域内土壤大多数为粉土、粉壤，黏粒含量大都在10%以下，而砂粒、粉粒、黏粒含量定和为1，因此砂粒和粉粒含量之间会呈现明显的负相关关系。在不显著水平下，pH与CEC的相关系数为−0.110呈现弱负相关性，其仅是在统计分析结果。在自然界中，随着pH升高土壤胶体中负电荷数量增加，CEC也会随之变大。这可能是因为研究区域内土壤性质差异较大导致。

Table 1. Description statistics of soil physico-chemical properties

表1. 土壤理化性质描述性统计

Table 2. Correlation analysis of soil physico-chemical properties

表2. 土壤理化性质相关性分析

注：*在0.05水平上显著相关，**在0.01水平上显著相关。

3.3. 土壤转化函数构建

3.3.1. MLR转换函数

在多元回归分析时需要满足的条件之一是变量总体服从正态分布。因此，利用K-S检验方法来验证数据是否符合正态分布。本研究中将变量进行对数转换后符合正态分布。表1中训练集进行多元逐步回归方程如公式(9)所示，测试集来进行预测CEC。回归方程的R²为0.52。

$\text{CEC}=0.415\ast \text{OM}-0.113\ast \text{sand}+0.480\ast \text{pH}+0.148\ast \text{clay}$ (9)

式中：OM为有机质含量；sand为砂粒含量；clay为黏粒含量。

3.3.2. BP-NN转换函数

根据公式(3)计算得到隐含层节点数范围为1~12，然后通过试凑法得到最佳隐含层神经元数量。误差随隐含层节点数的变化过程，误差随节点数增加呈现先增加后减少再增加的现象(见图2)。综合比较隐含层节点数的RMSE和MAE，当隐含层神经元数为9时，BP-NN的性能最好。因此，BP-NN的结构为4-9-1，即4个输入变量、9个隐含层神经元，1个输出变量。模型训练次数为10000次，训练精度为0.001，学习速率为0.01 s，隐含层、输出层传递函数为tansig，训练函数为traingdx。训练集用来训练BP-NN，测试集用来预测CEC。

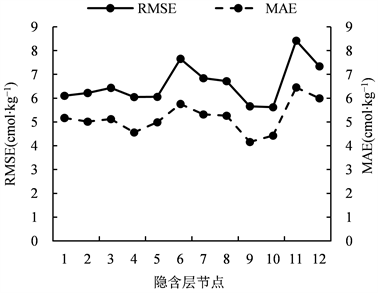
Figure 2. Influence of the number of neurons in the hidden layer on prediction accuracy

图2. 隐含层神经元节点数对预测精度的影响

3.3.3. SVM转换函数

在支持向量机中应用最广泛的高斯径向基核(RBF)函数，具有较宽的收敛域，且只含1个参数，易于优化 [17] ，选择SVM类型为支持向量回归(SVR)，核函数为径向基核函数，在RBF核函数中需要确定的参数是核函数的参数系数、惩罚因子c。本研究通过网格参数寻优来寻找一组最优的c、分别为1.00、0.33，训练精度设置为0.01。

3.4. 函数精度分析

MLR、BP-NN和SVM三种模型建立的PTFs用于预测测试集土壤样本CEC。测试集CEC的实测值与三种模型所得到的预测值之间的散点图见图3。BP-NN的MAE最小，表明BP-NN误差整体上小于SVM和MLR (见表3)。MLR、BP-NN、SVM三种模型的R²，其中SVM模型R²最大即自变量能解释因变量程度最高，BP-NN次之，MLR最低；SVM模型RMSE最小，BP-NN次之，MLR最大；SVM模型的Nash-Sutcliff效率系数E大于其他两种模型且都大于0小于1，表明三种模型的预测结果都接近于实测值的均值，其中SVM模型的效率系数为0.57拟合优度最高。

三种模型预测CEC较大值与较小值时有所欠缺(见图3)，这可能是由于模型中的训练集土壤类型不同、数量不足导致，当CEC处于15~25 cmol∙kg⁻¹范围，SVM能较好地预测CEC，BP-NN次之，MLR最差。综合考虑以上四个评价参数可知，SVM、BP-NN两种模型预测精度优于MLR，其中SVM、BP-NN的四个评价参数都较为接近，表明SVM模型的预测精度略优于BP-NN。

Table 3. Accuracy comparison of models

表3. 模型精度比较

(a) MLR 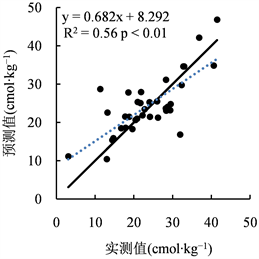(b) BP-NN (c) SVM

Figure 3. Scatter plots of measured and predicated values by models

图3. 不同模型实测值与预测值散点图

3.5. 函数敏感性分析

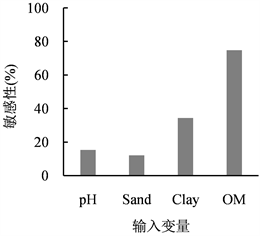
通过执行敏感性分析得到输入变量的相对重要程度。两种模型中输入变量pH、砂粒、黏粒、有机质对应的敏感性分别为15%、12%、34%、75%和24%、17%、26%、87% (见图4)，敏感性排序从大到小依次为有机质、黏粒、pH、砂粒。有机质在两个模型中都为最重要的变量，黏粒在BP-NN中的重要程度大于SVM。

4. 讨论

在相关性分析中，CEC与黏粒、有机质存在明显的正相关关系，其中有机质与CEC之间相关系数最大，表明CEC与有机质关系最为明显，其次为黏粒含量。这和前人的研究结果并不完全一致，例如Liao [3] 和Tang [10] 研究表明黏粒含量在预测CEC中起最主要的作用，有机质次之，而有些学者 [18] [19] 研究表明CEC主要受有机碳影响。这可能是因为在研究区域内有机质在研究区内变化明显，其变异系数远大于黏粒含量，且黏粒含量变程较小大都在10%以下。虽黏粒、有机质在不同研究中所起的主次要作用并不相一致，但都表明有机质和黏粒对CEC有明显的直接作用 [20] 。

SVM模型预测精度高于BP-NN、MLR模型，表明CEC与土壤理化性质存在非线性关系。这与国内外学者的研究不尽一致。Were [21] 和Liao [3] 发现SVM模型预测精度优于神经网络和多元回归。而Jafarzadeh等 [22] 比较支持向量机和神经网络两种模型的精度，研究表明神经网络模型精度要优于支持向量机。这可能是因为样本数量不同，模型输入变量有所差异导致。此外，与BP-NN相比，SVM有效地实现对基于小样本的高维非线性系统精确拟合，同时也避免了BP-NN存在的陷入局部最优解的问题，并且提高了泛化能力。由于土壤的异质性，想要在大尺度范围内测定土壤CEC是很困难的。因此，对于大尺度上数字土壤图的优化、作物模型等工作中，SVM可以提供比MLR和BP-NN更合理的CEC参数 [3] 。

从4个输入参数对输出变量CEC影响敏感性的统计分析角度看，影响较大的参数是有机质、黏粒，表明在预测CEC过程中模型的输入变量有机质、黏粒是最重要的两个变量。pH虽与CEC的相关性小于砂粒与CEC的相关性，但pH的敏感性要大于砂粒，这可能是因为砂粒对CEC的影响很小。

(a) BP-NN 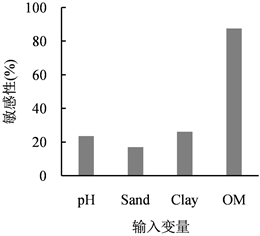(b) SVM

Figure 4. Sensitivity analysis of output variable (CEC) to the input variable of the models

图4. 输出变量(CEC)对模型输入变量的敏感性分析

5. 结论与展望

5.1. 结论

研究利用BP-NN、SVM、MLR三种方法选择pH、砂粒、粘粒、有机质含量为输入变量来预测旱作区土壤阳离子交换量。结果表明，在构建预测CEC的PTFs时有机质和黏粒是最重要的，应优先考虑；SVM和BP-NN两种方法在旱作区内预测土壤CEC是可行的，但是SVM、BP-NN在预测CEC较大值与较小值上不准确；利用SVM建立PTFs的精度略优于BP-NN，两者预测精度均优于MLR。基于支持向量机的土壤转换函数在旱作区内能够较好的预测阳离子交换量。

5.2. 展望

在本研究中，砂粒、黏粒、pH、有机质作为自变量变量，并没有考虑土壤黏土矿物类型、碳酸钙等含量，这些都对土壤CEC产生影响，在以后的研究中可进一步考虑它们。此外，有学者 [23] [24] 将土壤粒径的分形维数作为输入变量预测土壤CEC，以后的研究可将分形维数引入模型。

基金项目

煤科总院技术研发项目(2021-JSYF-007)；中煤科工集团创新创业重点项目(2019-ZD004)；国家重点研发计划项目(2016YFD0300801)。

NOTES

^*通讯作者。