考虑客货混合运输的城市轨道交通列车时刻表优化模型

Optimization Model of Urban Rail Transit Train Schedule Considering Passenger-Freight Coordination Transportation

摘要: 近年来城市交通网络负荷不断增加，我国城市交通拥堵问题日趋严重，城市地面物流运输效率低下，而城市轨道交通具有覆盖面广、运输量大、运输速度快等特点，可以利用剩余运力缓解城市物流配送的压力。基于城市轨道交通进行客货混合运输包括客货共车和客货分离等模式。在客货共车模式下，本文在满足原有乘客运输需求基础上进行货物运输，以货运成本最小化为目标，将给定的货单需求与列车匹配，分别考虑固定发车间隔与灵活发车间隔两种列车发车情况，构建了混合整数线性规划模型。以上海地铁13号线一期工程线路为案例，利用Cplex求解器进行数值实验，结果表明，本文建立的模型可以将客货需求与列车进行匹配，通过改变列车的发车时间、发车数量和客货列车的车厢分配，能够提高货运收益和客货运输效率，为轨道交通运营方提供了客货混合运输的可行性方法。

Abstract: In recent years, urban traffic load has been increasing, and the problems of urban traffic congestion have become increasingly serious in our country with Low efficiency of logistics and transportation, while urban rail transit has the characteristics of wide coverage, large transportation volume and fast transportation speed, etc. Therefore the surplus capacity of rail transit can be used to relieve the pressure of urban logistics distribution. The subway-based underground logistics system includes exclusive-train mode and train-sharing mode. Under the train-sharing mode, this paper carries out freight transportation on the basis of meeting the original passenger transportation demand, matches the given freight bill demand with the train aiming at minimizing the freight cost, considers two train departure situations, namely fixed departure interval and flexible departure interval, and presents a mixed integer linear programming model. In this study, the first phase of Shanghai Metro Line 13 is taken as an example, and the numerical experiments using solver Cplex show that the model can match the passenger and freight demand with the train. By changing the departure time and number of trains and the allocation of passenger and freight trains, the freight revenue and passenger and freight transportation efficiency can be improved, which provides a feasible method for rail transit operators to mix passenger and freight transportation.

1. 引言

进入新世纪以来，随着我国城市化进度加快，越来越多的人涌入城市，随之带来了城市土地资源紧缺，城市出行出现拥堵，出行成本增加。在有限的城市地面交通资源下，已经有许多城市采取“车牌号限行”的方式缓解城市交通拥堵，因而导致城市内部货物运输时效下降，物流成本节节攀升，城市地面运输方式似乎已到达难以优化的瓶颈阶段。据此，利用地下空间资源成为交通部门缓解交通问题的重要举措 [1] 。2018年，中国科协将未来城市地下交通及物流系统作为60个重大科学问题和重大工程技术难题之一 [2] 。因此，依托现有的城市地铁网络，在非高峰时段充分利用地铁线路的冗余运力，来发展地下物流网络与地铁协同运输，是当前更加可行的方案。忻剑鸣 [3] 针对现代物流发展的特点，提出了利用城市轨道交通网络发展物流业的设想，综合讨论了用轨道交通开展配送的优势及局限性。杨立春 [4] 从轨道交通客流在时间分布及空间分布的非均衡性出发，对轨道交通客运与货运的协同运行进行了探索性研究。谭寅亮等 [5] 提出了利用客运低谷实施物流快运的观点。乔俊杰等 [6] 提出了充分利用地铁的剩余运能来进行货物运输，并且探讨了地铁物流模式的发展优势和发展空间。Savelsbergh等 [7] 谈论了城市物流系统未来的机遇与挑战，并指出未来城市物流的最大机遇在于公共交通和城市货运的综合服务网络设计。Cochrane等 [8] 研究了公共交通货运服务在实际实施过程中的机遇与挑战。研究结果表明，客货共运系统将提升整个交通运输系统的效率，降低能源消耗和较少碳排放，但最关键的问题是如何在满足货运需求下仍然保障客运系统的服务水平。Ozturk [9] 等针对单向地铁线路货运的问题，在已知既有客运列车时刻表的前提下，考虑在两列车间插入一趟货运列车的形式，利用既有客运站台装卸货物，以最小化货物送达延迟时间为目标，构建了货运列车时刻表的混合整数优化模型。Li等 [10] 考虑客货共载和货运专列两种形式，优化了列车的停站方案和时刻表。邸振等 [11] 基于地铁线路的客货协同运输问题，考虑了客货需求在时间窗上的不同，以客运硬时间窗与货运软时间窗设置了延迟惩罚，提出了客货两方面供给和需求匹配的协同运输优化策略。戚建国等 [12] 基于灵活编组运营组织模式，研究轨道交通客货协同运输方案优化问题，建立了以乘客等待时间和运营公司运营成本最小化为目标的数学优化模型，对列车编组方案、列车运行图和客货运输方案进行协同优化决策。李竹君等 [13] 针对机场线客货共运问题提出了列车编组、停站、时刻表和货物分配的综合优化方法，对比了固定编组与灵活编组的客货混合运输情况，在货物时效要求高时，灵活编组的优势更加明显。

上述研究在城市轨道交通客货混合运输的可行性与运输策略方面提供了良好的理论支撑，但大多从原有列车运行基础上进行货物运输，改变列车发车时间的客货混合运输策略研究较少。鉴于此，本文构建了客货混合运输下的城市轨道交通列车发车时刻模型，在满足原有乘客运输需求的基础上，以改变列车发车间隔的方式探讨城市轨道交通客货共车模式需求匹配的协同运输优化策略。

2. 问题描述

轨道交通参与货物运输，其主要目的是利用列车非高峰时段的剩余运力缓解城市的货运压力。因此本文的研究时段为乘客非高峰时段，考虑在原有客运列车基础上进行货物运输，设定货运专用车厢，通过改变列车的发车时间，探讨固定发车间隔与灵活发车间隔情况下的发车情况，同时满足乘客与货物的运输需求。本文考虑一条单向的轨道交通线路，如图1所示，此线路沿途共设S个车站，列车由车站1出发，经过车站2、3、……、S-1等车站，最终到达终点站S。从第1个车站开始，到第S-1个车站为止，均为可能的发货站点；从第2个车站开始，到第S个车站为止，均为可能的收货站点。

Figure 1. Train diagram of rail transit

图1. 轨道交通列车运行图

为研究方便，设当日货运需求集合为D，其发货站点与收货站点随机给出。设定起始时刻为0，研究时段[0,T]并以 $\epsilon$ 为最小单位分成一系列间隔相等的时间点，可表示为： $T=\left\{\epsilon ,2\epsilon ,\cdots ,t\epsilon ,\cdots ,T\epsilon \right\}$ 。设列车发车时刻必须为 $\epsilon$ 的整数倍，为方便计算，令 $\epsilon =60\text{s}$ 。列车在发车节点中的某个时刻出发，从起点站1至终点站S完成货物运输任务，在考虑各列车安全运行的前提下保证客货列车运行，原始客运列车上行线路的时间运行如图2所示。

轨道交通列车引入货运服务可以提供货物运输新方式，改善提升线路运营效益，因而货运服务的目标为运营企业货运利润最大化。货运利润既包括服务货单需求所带来的收入，也包括引入货运服务所额外增加的运营成本。与乘客不同，货物需要人工协助进行搬运，因而必须考虑货物装卸成本。装卸成本由被服务的货单货运量和单位箱装卸成本决定。另外，在利用客运列车实现客货混载时，货物在车站的装卸时间不能超过客车在车站的停靠时间。货物在车站等待装车的过程，需暂存于车站内一段时间，因而与仓储场地和人工管理相关的仓储成本不能忽视。

Figure 2. Train working diagram of up line

图2. 列车上行线路运行时间图

为尽可能降低货运成本，应尽量满足货运需求。由于线路富余能力有限，较难满足所有货单需求，应根据线路富余能力情况，尽可能选择利润较大的货单，放弃部分时效要求较高且利润较低的货单。为增加货运收入，需根据不同时段货单起讫点和运输时效要求，合理设计列车的发车间隔，尽可能满足更多货单需求。为了降低车站仓储成本，需制定合理的货单分配方案，以避免所有大运量货单在车站集中仓储。此外，为了节省列车运行成本，需确定合适的列车编组数量与货运专用车厢数，在保证乘客运输需求的同时更好匹配列车货运能力和需求。

3. 模型设计

3.1. 问题假设

针对上述列车运行的描述及要研究的问题，提出如下假设：

1) 所有列车均由起点站运行至终点站，仅考虑单向轨道交通路线，不考虑列车折返情况。

2) 所有列车在不同区间的运行速度和时间均相同。

3) 轨道交通运营公司在一定时间段内开展货运服务，收集的货单有限，尽量满足货单需求。

4) 为方便计算，将货物同一化，不考虑货物间的区别，货物按重量以标准化单元作为最小运输单位。

5) 轨道交通运营公司收集的货单规定了到站时间、和起讫点车站，且各个站点的货物容量足够，不会出现库存货物超额堆积情况。

6) 由轨道交通运营公司规定货单客户方的取货时间，客户会在预计时间提走货物，因此只考虑货单在等待装车过程中在车站存储产生的仓储成本，不考虑运达车站后等待提取的仓储成本。

7) 货单的运输价格按距离计，以每单位货物每公里运输价格为标准，向客户货单收取运输费用。

8) 列车的总能力大于乘客总需求，保证到达车站的旅客都能被服务，在客流完全服务的基础上进行载货服务，且货物需求与乘客需求可以在极限情况下满足。

3.2. 变量定义

本文模型涉及到的指代符号、参数及决策变量如下表1。

Table 1. Description table of relevant parameters and variables of the model

表1. 模型相关参数及变量说明表

3.3. 模型构建

考虑一条轨道交通线路的上行方向，如图3所示，在图示时间域内，t时刻有一辆列车从站1发出，称此列车为列车t，可知在 $t+r{t}^{1,O}$ 时刻进入O站的乘客与货物需求恰好可以被列车t运输，为建模与计算方便，本文称 $t+r{t}^{1,O}$ 时刻进入O站的乘客与货物需求为 $n_t^{O,D}$ 、 $d_t^{O,D}$ 。此外，由于货单数量有限，与乘客需求不同，货单只在某些特定时刻产生货物OD运输需求，为建模与求解方便，如式(1)(2)，将货单的货运量 $d^{k,O_k,D_k}$ 匹配到 $d_t^{O,D}$ 中。

$d_{t_k}^{O_k,D_k}=d^{k,O_k,D_k},\forall k,O,D$ (1)

$d_{t_k}^{O_k,D_k}=d^{k,O_k,D_k},\forall k,O,D$ (2)

Figure 3. Description of train operation time and decision variables

图3. 列车运行时间与决策变量说明

3.4. 固定发车间隔的混合运输时刻表优化模型

在城市轨道交通运营过程中，列车在非高峰时段的运行间隔时间往往是固定的，本节探讨固定发车间隔下的客货混合运输的发车情况。

$\begin{array}{c}\min Z=C_{load}\underset{t=1}{\overset{T}{{\displaystyle \sum }}}\underset{O=1}{\overset{S-1}{{\displaystyle \sum }}}\underset{D=O+1}{\overset{S}{{\displaystyle \sum }}}{d}_{t,in}^{O,D}+C_h\underset{t=1}{\overset{T}{{\displaystyle \sum }}}{x}_t\\ +C_{inv}\left(\underset{O=1}{\overset{S-1}{{\displaystyle \sum }}}\underset{D=O+1}{\overset{S}{{\displaystyle \sum }}}\underset{t=1}{\overset{T}{{\displaystyle \sum }}}\left(t+r{t}^{1,O}\right)d_{t,in}^{O,D}+\underset{O=1}{\overset{S-1}{{\displaystyle \sum }}}\underset{D=O+1}{\overset{S}{{\displaystyle \sum }}}\underset{t=1}{\overset{T}{{\displaystyle \sum }}}\left(T-t\right)\left(d_t^{O,D}-\underset{t=1}{\overset{T}{{\displaystyle \sum }}}{d}_{t,in}^{O,D}\right)\right)\\ -p\underset{t=1}{\overset{T}{{\displaystyle \sum }}}\underset{O=1}{\overset{S-1}{{\displaystyle \sum }}}\underset{D=O+1}{\overset{S}{{\displaystyle \sum }}}{L}^{O,D}{d}_{t,in}^{O,D}\end{array}$ (3)

式(1)的目标是使整个客货混合运输系统的成本最低。第一项是货物装卸成本，第二项是列车运营成本，第三项是货物在站点的仓储成本，第四项是货物运输产生的收入。

约束条件：

$t_{load}\left(\underset{O=1}{\overset{s}{{\displaystyle \sum }}}{d}_{t,in}^{O,s}+\underset{D=s}{\overset{S}{{\displaystyle \sum }}}{d}_{t,in}^{s,D}\right)\le t_{open}^s,\forall t,s$ (4)

$\underset{i=t}{\overset{t-gap+1}{{\displaystyle \sum }}}{x}_i=1,\forall t\in \left[gap,T\right]$ (5)

$\underset{O=1}{\overset{s}{{\displaystyle \sum }}}\underset{D=s+1}{\overset{S}{{\displaystyle \sum }}}{n}_{t,in}^{O,D}\le Cap\left(f_0-f_1\right),\forall t,s$ (6)

$\underset{O=1}{\overset{s}{{\displaystyle \sum }}}\underset{D=s+1}{\overset{S}{{\displaystyle \sum }}}\theta d_{t,in}^{O,D}\le Cap\cdot f_1,\forall t,s$ (7)

$M\cdot \left(1-x_t\right)+\underset{1}{\overset{t}{{\displaystyle \sum }}}{d}_{t,in}^{O,D}\ge \underset{1}{\overset{t}{{\displaystyle \sum }}}{d}_t^{O,D},\forall t,\left(O,D\right)$ (8)

$\underset{1}{\overset{t}{{\displaystyle \sum }}}{d}_{t,in}^{O,D}\le \underset{0}{\overset{t}{{\displaystyle \sum }}}{d}_t^{O,D},\forall t,\left(O,D\right)$ (9)

$M\cdot \left(1-x_t\right)+\underset{1}{\overset{t}{{\displaystyle \sum }}}{n}_{t,in}^{O,D}\ge \underset{1}{\overset{t}{{\displaystyle \sum }}}{n}_t^{O,D},\forall t,\left(O,D\right)$ (10)

$\underset{1}{\overset{t}{{\displaystyle \sum }}}{n}_{t,in}^{O,D}\le \underset{0}{\overset{t}{{\displaystyle \sum }}}{n}_t^{O,D},\forall t,\left(O,D\right)$ (11)

$-d_t^{O,D}{x}_t+d_{t,in}^{O,D}\le 0,\forall t,\left(O,D\right)$ (12)

$-M{x}_t+n_{t,in}^{O,D}\le 0,\forall t,\left(O,D\right)$ (13)

$d_{t,in}^{O,D},n_{t,in}^{O,D}\ge 0,\forall t,\left(O,D\right)$ (14)

$t,O,D\in Z,0\le t\le T,1\le O\le S-1,2\le D\le S$ (15)

式(4)表示装卸作业时间约束，表示列车在每站的装货、卸货行为要在列车停站时间内完成；式(5)表示列车固定发车时间间隔约束；式(6)、(7)为列车客、货运载容量约束；式(8)、(9)、(10)、(11)为货物与乘客需求约束，保证需求 $d_t^{O,D},n_t^{O,D}$ 由列车t及后续列车完成；式(12)、(13)、(14)为决策变量约束，满足当 $x_t=1$ 时， $d_t^{O,D},n_{t,in}^{O,D}\ge 0$ ，当 $x_t=0$ 时， $d_t^{O,D},n_{t,in}^{O,D}=0$ ；式(15)为其余参数取值范围。

3.5. 灵活发车间隔的混合运输时刻表优化模型

由于到达车站的OD客流存在不确定性，因此以固定间隔发车会造成客流与货流的不均衡，不一定能够满足客流与货物需求，因此本节探讨灵活发车间隔下的客货混合运输的发车情况。

灵活发车间隔下，将式4修正为

$\underset{i=t}{\overset{t-ga{p}_{\min }+1}{{\displaystyle \sum }}}{x}_i\le 1,\forall t\in \left[ga{p}_{\min },T\right]$ (16)

$\underset{i=t}{\overset{t-ga{p}_{\max }+1}{{\displaystyle \sum }}}{x}_i\ge 1,\forall t\in \left[ga{p}_{\max },T\right]$ (17)

表示相邻列车的发车时间间隔在最小运行间隔和最大运行间隔之间。由此得灵活发车模式下的发车时刻表优化模型为：

目标函数：式(3)

约束条件：式(4)，式(6)~式(17)

4. 算例分析

为了测试上述模型设计的有效性，本节设计了一个具体的算例，并使用Matlab2018a软件调用CPLEX12.6求解器对其进行求解。实验在配置AMD Ryzen 7 4800处理器和16 GB机带RAM的笔记本电脑上进行。本采用上海地铁13号线一期工程金运路至长寿路段为研究对象 [14] ，数据来自2015年4月1日至4月30日上海轨道交通刷卡AFC数据集，该线路共10个站点，如图4所示。

Figure 4. Schematic diagram of shanghai metro line 13 phase 1

图4. 上海地铁13号线一期示意图

4.1. 算例概况与参数设置

在上海地铁13号线一期线路算例中，地铁里程共15公里，对该线路客流数据进行统计分析，随机收集工作日十天上行方向的入站客流平均值，分别以1 h和1 min为单位得到进站客流在时间上的分布情况，如图5所示，始发站金运路站的进站客流具有突出的早高峰与平峰特征，祁连山南路站、真北路站的进站客流具有明显的早、晚高峰与平峰特征，该地铁线路客流谷峰明显，具有明显的通勤特征。

(a) 13号线小时进站客流变化情况(b) 站1(金运站)分钟进站客流变化情况

Figure 5. Inbound passenger flow in the upward direction of Line 13

图5. 13号线上行方向入站客流情况

Figure 6. Hourly OD passenger flow distribution

图6. 小时OD客流分布情况

13号线在非高峰时期的列车运营间隔为8~10分钟，本文考虑列车运行时段为早高峰结束后的10:00至11:00，为非高峰时间的1 h，该线路乘客数据取自票务系统内的AFC历史刷卡数据，在考虑的时间段内包含了52个OD的乘客需求，合计4675位乘客，时段内不同OD客流需求的时空分布如图6所示。

该线总计运行时长约25 min，地铁列车在每一站的停站时间和至相邻车站的运行时间如表2所示。

Table 2. Stop time and operation time of metro line 13

表2. 地铁13号线列车停站时间与运行时间

地铁线路大多为6编组列车，额定容量计每节200人，则最大容量为1200人，设其中1节车厢专门用于货物运输。为便于分析，一个货运车厢的广义操作成本设置为500元，轨道交通公司向货运需求方收取每单位箱每单位距离50元；每单位箱每分钟产生的库存成本为6元，其余具体的参数设置如表3所示。

Table 3. Example parameter setting

表3. 算例参数设置

由于现实中本线路没有开展货运业务，因此本文设计了分时货单，为保证货单在此时段内可以完成发货，将发货站点设置在站1~站5之间，将收货站点设置在站4~站10之间，货单进站时间随机分布在[0,40]之间。为模拟货单的分散与集中情况，为发货站点1设置4组货单需求，其余发货站点的货单需求不超过2组，货单共10组OD货运需求，总计391单位箱货物，货单具体情况如表4所示。

Table 4. Goods order demand table

表4. 货单需求表

4.2. 优化结果分析

在上述参数设置下，可以得到固定发车间隔下的发车情况和货单完成情况，如表5所示。在原发车间隔10 min的情况和本文的货单需求情况下，地铁运营方在60 min内可完成252.5单位货物运输需求，收益为37,853.8元。当列车以固定时间间隔运行时，改变运行的间隔时间，在给定时段内会多发列车，本文讨论了在最小运行间隔5 min与实际运行间隔10 min之间的运营情况分析，可知在列车间隔时间gap ≥ 6时，无法完成全部货物运输需求，系统总收益随运行间隔的减小而增大，列车随着运行间隔的减小能够运输更多的货物，在接受订单后库存成本变动大的原因是本文设置未运输的货物会一直堆放直至时段结束，产生的库存成本较大，因此库存成本会随缺运量的增加而大幅提升。

Table 5. Completion of departure and goods order under fixed departure interval

表5. 固定发车间隔下的发车与货单完成情况

对于发车间隔gap为5和6分钟的发车情况进行分析，得到的列车运行时刻表如图7、图8所示，图中货单的黑色实线表示货单到达发货站点的时间，蓝色实线表示列车装载货物，图中给出列车完成货单需求的情况。在gap = 6情况下，共发出10辆列车，所有列车都参与了货物运输，货单需求没有全部

Figure 7. Train departure and cargo list with departure interval of 5

图7. 发车间隔为5时的列车发车与货单情况

满足，受列车运载能力和停站时间影响，货单8与货单10产生了缺运现象，以货单9为例，第6、8、9、10辆列车完成了货单9 的运输需求，第7辆列车受容量限制，在到达车站3时已经满载，无法运输货单9的货物，货单2、7、9均产生了类似的跨列车运输现象，使货单的库存成本变大。产生跨列运输现象的原因是列车进站前货物容量已经满载或后续车站货单的运输收益更高使列车优先完成收益更高的货单。在gap = 5情况下，共发出12辆列车，货单需求被全部满足，第12辆列车没有参与货物运输，货单2、7、9、10产生了跨列车运输现象，但由于发车间隔的缩短，货物的等待时间减小使库存成本减少，货运量的增加使运输收益增加，轨道交通运营方的总收益增大。

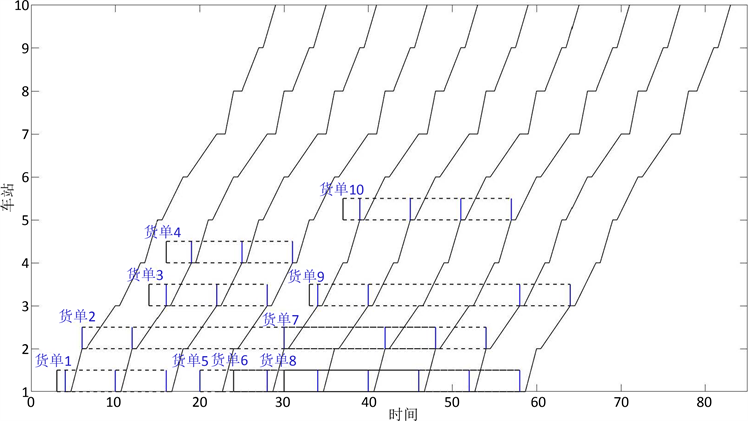
Figure 8. Train departure and cargo list with departure interval of 6

图8. 发车间隔为6时的列车发车与货单情况

在上述参数设置下，可以得到灵活发车间隔下的发车情况和货单完成情况，如表6所示。在灵活发车间隔情况下，列车间的发车间隔不定，共发出11辆列车，系统总收益为116,818元，相比固定发车间隔5 min时的最优情况少开行1辆列车，增加了1380元的收益，发车成本减少800元，库存成本减少了580元。货运车辆当货运车厢增开到4节时，剩余2节客运车厢已无法满足原有的客流需求，因此出现无解情况。轨道交通运营方可以根据实际情况调整列车的发车间隔与开行数量，在本文的客货需求与成本等参数条件下，固定发车间隔的最优收益与灵活发车间隔的最优收益差距不大。

Table 6. Departure and goods order completion under flexible departure interval

表6. 灵活发车间隔下的发车与货单完成情况

对于灵活发车间隔的发车情况进行分析，灵活间隔下最优的发车时刻为：4、9 、14、20、26、31、36、41、46、51、56，其发车间隔均为5 min或6 min。在灵活发车间隔情况下，货单仍会产生跨列车运输现象，因此改变货运车厢数以扩大列车货物容量，得到的列车运行时刻表如图9、图10所示。当货运

Figure 9. Condition of train departure and cargo list with flexible departure interval when f₁=1

图9. f₁=1时灵活发车间隔的列车发车与货单情况

Figure 10. Condition of train departure and cargo list with flexible departure interval when f₁=2

图10. f₁=2时灵活发车间隔的列车发车与货单情况

车厢由1节扩大到2节时，所有货单均未产生跨列车运输现象，库存成本降低了21%，由24,482元降低到199,332元，系统总收益扩大到121,968元。当货运车厢扩大到4节时，优化模型无解，原因是此时客运车厢减小到2节，无法完成原有的客运需求。综合以上情况，在本文的客货需求与参数设置情况下，灵活发车间隔模式且货运车厢数为2时，轨道运营方的总收益最大，可以在完成原有乘客运输需求的同时完成给定的货单需求，可以防止货物的跨列车运输现象，为轨道交通的客货混合运输提供了新的思路与方法。

4.3. 货运灵敏度分析

为了对比固定发车间隔模式与灵活发车间隔模式在不同货物需求情况下的情况，本节将分2组实验进行分析，每组实验设置10个货运OD，设计4组货单需求如表7所示，探讨货运量、货单OD聚集程度和客货车厢分配情况对整个系统的影响。第1组实验货运量服从N(20,64)的正态分布，表示货运量少的情况；第2组实验随机选取货运量服从N(40,64)的正态分布，表示货运量较多的情况；两组实验将比较分析固定发车间隔与灵活发车间隔，货运车厢不同情况的优化方案利润，分析不同列车发车方案与货运需求和供给的关系。

Table 7. Goods order OD demand table

表7. 货单OD需求表

为了对货单OD的聚集程度进行模拟，对货单需求表做如下设置。货单集合1的OD站点较均匀的分布在站点中，模拟货单O点与D点均较为分散的情况；货单2的O点集中分布在前5个站点，D点较均匀分布，模拟货单O点聚集D点分散的情况；货单3的O较均匀分布，D点集中分布在后5个站点，模拟货单O点分散D点聚集的情况；货单4的O点集中分布在前5个站点，D点集中分布在后5个站点，模拟货单O点与D点均较为聚集的情况。

分别对不同情况求最优解，所有情况均能在2min内获取最优解，最终收益状况如图11、图12所示。

在图11中，货单货运量较小，所有情况均未产生货物缺运现象，仅1节货运车厢可满足所有的货物需求。当货运车厢增加为2节时，总运营收益未发生变化，说明此时制约总收益的不是货运容量。随着货单OD的变化，总运营收益随运输里程的增加而增加。对比图11与图12，货运量接近翻倍情况下，货单集合1的运营收益也几乎增加了1倍。但由于货单集合2、3、4均有OD站点的聚集情况，产生的不同程度的货物缺运现象，可以明显的看出，相同货运量水平情况下，货物在发货站点聚集更容易造成货物缺运现象，且货单2中所有缺运情况均相同，货运容量扩大仍不能改善缺运现象，原因是在货运量较大且发货聚集在同一站点情况下，制约轨道交通货物运输能力的是停站时间，有限的停站时间不能满足聚集的货物需求。在货单集合3高货运量的固定发车间隔模式下，增加货运车厢使货物缺运量由30下降到19，说明此时货运容量与停站时间都对货物运输能力产生了影响。

Figure 11. Revenue comparison under different cargo orders (freight volume follows N (20,64) distribution)

图11. 不同货单情况下的收益对比(货运量服从N(20,64)分布)

Figure 12. Revenue comparison under different cargo orders (freight volume follows N (20,64) distribution)

图12. 不同货单情况下的收益对比(货运量服从N(40,64)分布)

通过以上的分析可以看出，在低运量货单情况下，列车的运输能力足够富余，不同聚集程度的货运OD需求均可以被满足。而在高运力货单情况下，货运O点聚集程度高的货单集合更容易产生缺运现象，改变货运容量对改善运营情况的收益不显著，列车的停站时间是制约运输能力的关键因素。由于本节以最小发车间隔gap = 5 min为固定发车间隔，灵活发车间隔模式虽具有更高的总运营收益，但与固定发车间隔模式的发车数与货物库存时间相差不大，两种模式的运营收益差距较小，但对比不同聚集程度的货单集合，灵活发车间隔模式的发车数量少，产生的缺运量更小。

5. 结论

本文针对固定发车间隔与灵活发车间隔两种列车运行条件，探讨了城市轨道交通客货混合运输的可行性方案，构建了混合整数线性规划模型。以上海地铁13号线一期线路为例，使用Matlab语言调用Cplex求解器进行了数值实验。实验结果表明：1) 本文提出的方法能够实现轨道交通线路对客货混合运输的需求匹配，在满足原有乘客需求的基础上最大限度完成给定货单的货物需求；2) 通过固定发车间隔与灵活发车间隔两种发车策略，确定不同条件下列车开行的数量与发车时间，实现货单与列车的匹配；3) 对客货运输中的货运车厢数进行控制，改变列车的客、货运容量，尽可能减少跨列车运输现象，可以得到系统总成本最低的最优解，为轨道交通客货混合运输提供了新方法。

当前，国内外对于城市轨道交通客货协同优化方面的研究仍处于初步阶段，还有许多相关问题需要进一步研究。本文仅仅着眼于地铁客货运输线路上综合成本最小化，对于不同部分成本的度量仍有不足之处；本文的乘客需求是由数据集给定的，而实际的乘客需求是动态变化的；本文只考虑了单向列车线路，实际列车运行是下行线路与上行线路并存的，改变上行线路的列车数量与发车时间，对应的下行线路也会发生变化；在本文研究过程中发现，停站时间对车站装载货物的限制十分明显，对停站时间进行优化是未来研究的一个新方向；另外，本文假设的运输条件较为苛刻，整个运输系统的鲁棒性也是值得进一步研究的问题。

基金项目

国家自然科学基金项目(72021002)。